خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ضرب اعداد اعشاری و درصدها در مسائل داستانی

در بخش قبلی، به شما نشان دادم که چگونه کلمۀ "از" در یک مساله داستانی مرتبط با کسرها، معمولاً معنای عملیات ضرب را می دهد. این ایده در مورد مسائل داستانی مرتبط با اعداد اعشاری و درصدها نیز صحیح است. روش حل کردن این دو نوع مساله شبیه یکدیگر می باشد، پس در این آموزش از روی آن می پرم.

یک نوع رایج از مساله ها یک مقدار اولیه به شما می دهد - و یک سری اطلاعات دیگر - و از شما می پرسد چقدر در نهایت باقی می ماند. در اینجا یک مثال از این نوع داریم:
در ابتدا، یک معادله کلمه تشکیل بدهید تا مشخص گردد ماریا چقدر پول در بانک گذاشته است:
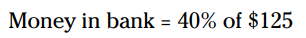
برای حل این معادله کلمه، درصد را به عدد اعشاری تغییر بدهید و کلمۀ "از" (of) را به علامت ضرب تبدیل کنید. سپس ضرب را انجام دهید:
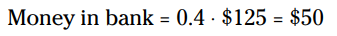
از آنجا که ماریا با مبلغ 125$ آغاز کرده بود، بنابراین 75$ برای خرج کردن باقیمانده است:
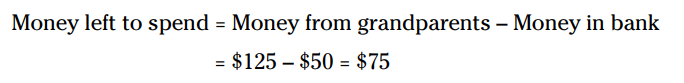
مساله می گوید ماریا 35% از این مبلغ باقیمانده را صرف خرید یک جفت کفش کرده است. دوباره، درصد را به اعشار تبدیل کنید و کلمۀ "از" را به علامت ضرب تبدیل نمایید:
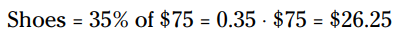
او بقیۀ پولش را صرف خرید لباس کرده است، بنابراین:
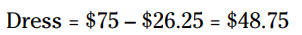
بنابراین، ماریا 48.75$ صرف خرید لباس کرده است.
برخی مسأله ها مبلغ نهایی باقیمانده را به شما می دهند و از شما می خواهند پیدا کنید که مبلغ آغازین چقدر بوده است. به طور کلی، این نوع مساله ها سخت تر هستند، چون شما معمولاً رو به سمت عقب فکر نمی کنید. در اینجا یک مثال داریم، و البته از نوع سختش هم می باشد، پس کمربند ایمنی خود را ببندید:
این مساله، مشابه مثال قبلی است، اما در اینجا باید از انتها شروع کنید و به وارونه کار کنید. توجه کنید که تنها مبلغ دلاری مسأله بعد از دو مقدار درصدی می آید. مساله به شما می گوید که ماریا بعد از دو تراکنش - قرار دادن پول در بانک و خرید یک کیف پول - به 12$ می رسد، و از شما می خواهد که پیدا کنید مبلغ اولیه چقدر بوده است.
برای حل کردن این مساله، دو معادلۀ کلمه (word equations) ایجاد کنید تا دو تراکنش را توصیف کند:
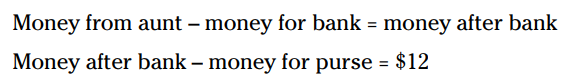
توجه کنید که این دو معادلۀ کلمه چه می گویند. اولین معادله به شما می گوید، ماریا پول را از عمه اش گرفته است (Money from aunt)، بخشی از آن را در بانک گذاشته است (money for bank)، در نتیجه مقداری پول برایش باقی مانده است که من آن را پول بعد از بانک (money after bank) نامیده ام. دومین معادله کلمه در جایی آغاز می شود که اولین معادله خاتمه یافته است. معادلۀ دوم به شما می گوید، ماریا از پول باقیمانده از بانک، یک کیف پول می خرد و در نهایت 12$ برایش باقی می ماند.
این معادلۀ دوم هم اکنون یک مقدار پولی در خودش دارد، پس از اینجا آغاز کنید. برای حل این مساله، متوجه می شوید که ماریا 75% از پولش را در زمان خرید کیف پول، هزینه کرده است. یعنی، این 75% را از پولی که بعد از بانک برایش مانده است هزینه کرده است.
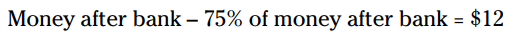
من می خواهم یک تغییر کوچک در این معادله بدهم، تا بدانید این معادله دقیقاً چه می گوید:
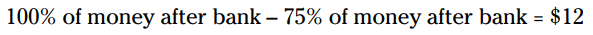
با این حال، در این مورد خاص، قرار دادن 100% به شما کمک می کند تا ارتباط معنا داری را ایجاد کنید.

قبل از ادامۀ کار، ابتدا مطمئن شوید که مراحلی را که شما را تا اینجای کار آورده اند به درستی درک کرده اید. دایرۀ درصد (percent circle) به شما می گوید که: (در فصل 12 در مورد دایرۀ درصد می توانید بیشتر بدانید)
اوکی، الان می دانید که ماریا بعد از بانک، چقدر پول دارد، کافیست این عدد را در معادلۀ اول بگنجانید:
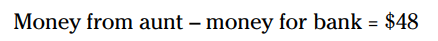
الان، شما می توانید با طرز فکر مشابهی، این معادله را حل کنید:
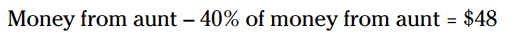
دوباره معادله را باز نویسی کنید تا واضح تر گردد:
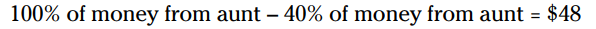
با توجه به اینکه:
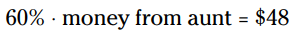
در این مرحله، برای حل معادله می توانید از دایرۀ درصد استفاده کنید (شکل 1-13 را ببینید). در این مورد، دایرۀ درصد به شما می گوید:

نکته: شما به سادگی می توانید مساله های داستانی شامل درصد را با تبدیل درصدها به اعداد اعشاری حل کنید. (برای جزئیات چگونگی این کار فصل 12 را ببینید). در اینجا چند درصد رایج و معادل اعشاری آنها را داریم:

پیدا کردن اینکه چقدر پول باقی مانده است
یک نوع رایج از مساله ها یک مقدار اولیه به شما می دهد - و یک سری اطلاعات دیگر - و از شما می پرسد چقدر در نهایت باقی می ماند. در اینجا یک مثال از این نوع داریم:
پدر بزرگ و مادر بزرگ ماریا (Maria) در روز تولدش به او 125$ دادند. او 40% از پول را در بانک (bank) پس انداز کرد، سپس 35% از باقیماندۀ پول را برای یک جفت کفش (shoes) هزینه کرد، و بقیه پول را صرف خرید یک لباس (dress) کرد. قیمت لباس چقدر شده است؟
در ابتدا، یک معادله کلمه تشکیل بدهید تا مشخص گردد ماریا چقدر پول در بانک گذاشته است:
برای حل این معادله کلمه، درصد را به عدد اعشاری تغییر بدهید و کلمۀ "از" (of) را به علامت ضرب تبدیل کنید. سپس ضرب را انجام دهید:
نکته: توجه ویژه ای به اینکه چیزی که مشغول محاسبه اش هستید استفاده شده است یا اینکه باقی مانده است داشته باشید. اگر نیاز داشته باشید که تا بخش باقیمانده کار کنید، ممکن است مجبور شوید آن را از مبلغی که با آن آغاز کرده بودید تفریق کنید.
از آنجا که ماریا با مبلغ 125$ آغاز کرده بود، بنابراین 75$ برای خرج کردن باقیمانده است:
مساله می گوید ماریا 35% از این مبلغ باقیمانده را صرف خرید یک جفت کفش کرده است. دوباره، درصد را به اعشار تبدیل کنید و کلمۀ "از" را به علامت ضرب تبدیل نمایید:
او بقیۀ پولش را صرف خرید لباس کرده است، بنابراین:
بنابراین، ماریا 48.75$ صرف خرید لباس کرده است.
پیدا کردن اینکه مبلغ اولیه چقدر بوده است
برخی مسأله ها مبلغ نهایی باقیمانده را به شما می دهند و از شما می خواهند پیدا کنید که مبلغ آغازین چقدر بوده است. به طور کلی، این نوع مساله ها سخت تر هستند، چون شما معمولاً رو به سمت عقب فکر نمی کنید. در اینجا یک مثال داریم، و البته از نوع سختش هم می باشد، پس کمربند ایمنی خود را ببندید:
ماریا مقداری پول در روز تولدش از عمّه اش دریافت کرد. او طبق عادتش 40% آن را در بانک (bank) پس انداز کرد، و با 75% از باقیمانده پولش یک کیف پول (purse) خرید، و وقتی کارش تمام شد، او 12$ برای صرف شام داشت. عمّه اش چقدر پول به او داده بود؟
این مساله، مشابه مثال قبلی است، اما در اینجا باید از انتها شروع کنید و به وارونه کار کنید. توجه کنید که تنها مبلغ دلاری مسأله بعد از دو مقدار درصدی می آید. مساله به شما می گوید که ماریا بعد از دو تراکنش - قرار دادن پول در بانک و خرید یک کیف پول - به 12$ می رسد، و از شما می خواهد که پیدا کنید مبلغ اولیه چقدر بوده است.
برای حل کردن این مساله، دو معادلۀ کلمه (word equations) ایجاد کنید تا دو تراکنش را توصیف کند:
توجه کنید که این دو معادلۀ کلمه چه می گویند. اولین معادله به شما می گوید، ماریا پول را از عمه اش گرفته است (Money from aunt)، بخشی از آن را در بانک گذاشته است (money for bank)، در نتیجه مقداری پول برایش باقی مانده است که من آن را پول بعد از بانک (money after bank) نامیده ام. دومین معادله کلمه در جایی آغاز می شود که اولین معادله خاتمه یافته است. معادلۀ دوم به شما می گوید، ماریا از پول باقیمانده از بانک، یک کیف پول می خرد و در نهایت 12$ برایش باقی می ماند.
این معادلۀ دوم هم اکنون یک مقدار پولی در خودش دارد، پس از اینجا آغاز کنید. برای حل این مساله، متوجه می شوید که ماریا 75% از پولش را در زمان خرید کیف پول، هزینه کرده است. یعنی، این 75% را از پولی که بعد از بانک برایش مانده است هزینه کرده است.
من می خواهم یک تغییر کوچک در این معادله بدهم، تا بدانید این معادله دقیقاً چه می گوید:
یادتان باشد: اضافه کردن 100% "از" (of) معادله را تغییر نمی دهد، چرا که به معنای ضرب کردن در 1 می باشد. در واقع، شما می توانید این کلمه را در هر جایی که بخواهید از قلم بیندازید و آنچه می گویید تغییری نکند، فکرش را بکنید مدام آن را بگوییم، صحبتهایمان مسخره می شود "دیشب، من با 100% از ماشینم رانندگی کردم و از محل کارم به منزلم رفتم، با 100% از سگم پیاده روی کردم، سپس 100% از همسرم را با خودم همراه کردم تا 100% از یک فیلم را ببینیم."
با این حال، در این مورد خاص، قرار دادن 100% به شما کمک می کند تا ارتباط معنا داری را ایجاد کنید.
100% – 75% = 25%با استفاده از این ارتباط، معادله را به شکل زیر باز نویسی می کنیم:
قبل از ادامۀ کار، ابتدا مطمئن شوید که مراحلی را که شما را تا اینجای کار آورده اند به درستی درک کرده اید. دایرۀ درصد (percent circle) به شما می گوید که: (در فصل 12 در مورد دایرۀ درصد می توانید بیشتر بدانید)
$12 ÷ 0.25 = $48
اوکی، الان می دانید که ماریا بعد از بانک، چقدر پول دارد، کافیست این عدد را در معادلۀ اول بگنجانید:
الان، شما می توانید با طرز فکر مشابهی، این معادله را حل کنید:
دوباره معادله را باز نویسی کنید تا واضح تر گردد:
با توجه به اینکه:
100% – 40% = 60%دوباره معادله را باز نویسی می کنیم:
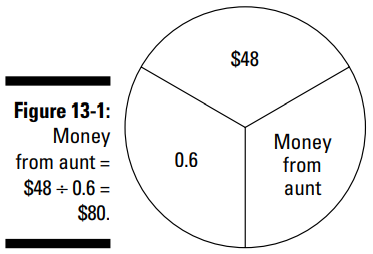
در این مرحله، برای حل معادله می توانید از دایرۀ درصد استفاده کنید (شکل 1-13 را ببینید). در این مورد، دایرۀ درصد به شما می گوید:
$48 ÷ 0.6 = $80بنابراین عمّۀ ماریا در روز تولدش به او $80 داده بود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: