خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
عملیات با اعداد علامت دار (Signed Numbers)

اگر در یک ساختمان که چهار طبقه بالای طبقه همکف و پنج طبقه زیر سطح زمین دارد، در آسانسور باشید، شما یک زمان عالی دارید که می توانید تمام روز را آسانسور سواری کنید و دکمه ها را فشار دهید، و به صورت واقعی با عملیات اعداد علامت دار (signed numbers) کار کنید. اگر از طبقه سوم زیر زمین بخواهید پنج طبقه بالا بروید، در نهایت به طبقه دوم بالای همکف می رسید.

شما احتمالاً خیلی جوانتر از آن هستید که یادتان بیاید، اما زمانی واقعاً مردم برای آنکه تمام روز آسانسور سواری کنند و دکمه ها را فشار بدهند، پول پرداخت می کردند! شاید هم مشغول تمرین جبر بودند!
هنگامیکه معلم کلاس اولتان به شما یاد می داد 1 + 1 می شود 2، احتمالاً به شما نگفت که این فقط یک بخش از کل داستان عملیات جمع می باشد. معلمتان احتمالاً اشاره ای نکرده است که اضافه کردن یک عدد مثبت به یک عدد مثبت دیگر در واقع یک مورد خاص است. اگر او به شما کل داستان را می گفت که شما می توانید اعداد مثبت و منفی را با یکدیگر جمع کنید یا ترکیبی از آنها را با یکدیگر جمع کنید، شما احتمالاً کیف کوچک مدرسه و ساندویچ ناهارتان را جمع می کردید و برای همیشه مدرسه را ترک می کردید.
اضافه کردن اعداد مثبت به اعداد مثبت تنها یک بخش کوچک از کل داستان جمع می باشد، اما در آن زمان برای شروع کفایت می کرده است. در این بخش کل آن داستان را برایتان تعریف می کنیم، تمامی اطلاعاتی را که نیاز دارید تا اعدادی با هر نوع علامت را با یکدیگر جمع کنید. اولین چیزی که در جمع اعداد علامت دار باید در نظر بگیریم اینست که با ساده ترین وضعیت آغاز کنیم - هنگامی که اعداد دارای علامت یکسان می باشند. ببینید چه اتفاقی می افتد:
فرض کنید مشغول جمع زدن 3- و 2- هستید. علامت ها یکسان هستند. شما ابتدا حاصل جمع 3 و 2 را پیدا می کنید که 5 می شود. چون علامت اعداد منفی بوده است، پس علامت پاسخ نیز منفی خواهد شد.
در اینجا چند مثال دیگر داریم:
همانطور که دیدید، جمع کردن اعداد دارای علامت یکسان کار بسیار آسانی بود.
آیا رابطه بین لئو (Leo) و جمینای (Gemini) به نتیجه می رسد؟ من پاسخ این سوال را نمی دانم، اما می دانم که جمع اعداد دارای علامت های متفاوت به نتیجه زیبایی می رسد. شما فقط کافیست چگونگی محاسبه را بدانید، و در این بخش من به شما می گویم.
ببینید هنگام جمع اعداد دارای علامت متفاوت چه اتفاقی می افتد:
در اینجا چند مثال دیگر از پیدا کردن حاصل جمع اعداد دارای علامتهای متفاوت را می بینید:
تفریق اعداد علامت دار واقعاً کار ساده ای می باشد: به جای اینکه یک مجموعه از قوانین جدید را برای تفریق اعداد علامت دار اختراع کنند، ریاضیدانان متوجه شدند که ساده تر اینست که مسائل تفریق را به مسائل جمع تبدیل کنند، و از قوانینی که برای جمع کردن وجود دارد استفاده کنند.
برای یک لحظه روش تفریق اعداد علامت دار را در نظر بگیرید. فقط مسأله تفریق را به یک مسأله جمع تبدیل کنید؟ زیاد معنادار به نظر نمی رسد؟ همه می دانند که شما نمی توانید فقط یک علامت عملیات حسابی را تغییر بدهید و انتظار داشته باشید که همان پاسخ یا پاسخ صحیح را بدست آورید. شما از خیلی وقت پیش می دانید که 4 - 10 با 4 + 10 یکسان نمی باشد. شما نمی توانید فقط عملیات را تغییر بدهید و انتظار پاسخ صحیح را هم داشته باشید.
خوب، برای اینکه روش بدرستی کار کند، شما در واقع دو چیز را تغییر می دهید. (تقریباً به نظر می رسد این مسأله جملۀ معروف "تکرار دو اشتباه منجر به یک کار درست نمی شوند" را باطل میکند، آیا اینطور نیست؟)
مثالهای زیر فرآیند تفریق اعداد علامت دار را در شرایط زندگی واقعی قرار می دهد:
در اینجا چند مثال از تفریق اعداد علامت دار داریم:
ضرب و تقسیم اعداد علامت دار واقعاً ساده ترین کار ممکن می باشند. تا زمانی که شما بتوانید ضرب و تقسیم را انجام بدهید، قوانین نه تنها ساده هستند، بلکه در مورد هر دو عملیات یکسان می باشند.
بورس را در نظر بگیرید (چیزی که این روزها زیاد در نظر گرفته می شود). خبرنگار اعلام می کند "داو جونز" (Dow Jones) در یک ردیف دوبار 20 امتیاز پایین رفت. شما دو مرتبه 20- را در یک در یکدیگر ضرب می کنید تا 40- را به دست آورید. بنابراین حاصلضرب یک عدد منفی به تعداد دفعات مثبت، منفی می باشد.
در مورد تقسیم چطور؟ شما و سه تا از دوستانتان تصمیم می گیرید تا برای دوست دیگری ناهار بخرید. قیمت ناهار 23.64$ می باشد. هر نفر چقدر باید مشارکت کند؟ عدد 23.64- را بر 4 تقسیم کنید، و میزان مشارکت هر نفر 5.91- خواهد بود.
توجه کنید که در کدام موارد پاسخ مثبت و در کدام موارد پاسخ منفی می باشد. شما می بینید که هنگامی که یک عدد مثبت و یک عدد منفی داشته باشید، تفاوتی نمی کند که عدد منفی اول آمده باشد یا دوم. همچنین، توجه کنید که ضرب و تقسیم مانند همان ضرب و تقسیم همیشگی هستند و تفاوتی نمی کنند، فقط علامت ها در اینجا باید مورد توجه قرار بگیرند.
در اینجا چند مثال از ضرب و تقسیم اعداد علامت دار داریم:
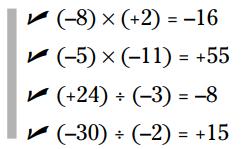
در موقعی که چندین عدد را در یکدیگر ضرب یا تقسیم می کنید یا ترکیبی از چند ضرب و تقسیم را یکجا دارید، می توانید این عملیات ها را با استفاده از قوانین زوج-فرد زیر ترکیب کنید.
در اینجا چند مثال از ضرب و تقسیم مجموعه ای از اعداد علامت دار را می بینید:

شما احتمالاً خیلی جوانتر از آن هستید که یادتان بیاید، اما زمانی واقعاً مردم برای آنکه تمام روز آسانسور سواری کنند و دکمه ها را فشار بدهند، پول پرداخت می کردند! شاید هم مشغول تمرین جبر بودند!
جمع اعداد هم علامت
هنگامیکه معلم کلاس اولتان به شما یاد می داد 1 + 1 می شود 2، احتمالاً به شما نگفت که این فقط یک بخش از کل داستان عملیات جمع می باشد. معلمتان احتمالاً اشاره ای نکرده است که اضافه کردن یک عدد مثبت به یک عدد مثبت دیگر در واقع یک مورد خاص است. اگر او به شما کل داستان را می گفت که شما می توانید اعداد مثبت و منفی را با یکدیگر جمع کنید یا ترکیبی از آنها را با یکدیگر جمع کنید، شما احتمالاً کیف کوچک مدرسه و ساندویچ ناهارتان را جمع می کردید و برای همیشه مدرسه را ترک می کردید.
اضافه کردن اعداد مثبت به اعداد مثبت تنها یک بخش کوچک از کل داستان جمع می باشد، اما در آن زمان برای شروع کفایت می کرده است. در این بخش کل آن داستان را برایتان تعریف می کنیم، تمامی اطلاعاتی را که نیاز دارید تا اعدادی با هر نوع علامت را با یکدیگر جمع کنید. اولین چیزی که در جمع اعداد علامت دار باید در نظر بگیریم اینست که با ساده ترین وضعیت آغاز کنیم - هنگامی که اعداد دارای علامت یکسان می باشند. ببینید چه اتفاقی می افتد:
-
شما سه CD دارید و دوست شما چهار CD دیگر نیز به شما می دهد:
(+3) + (+4) = +7
حالا شما هفت CD خواهید داشت.
-
شما به جان (Jon) مبلغ 8$ بدهکارید و 2$ دیگر هم از او قرض می گیرید:
(–8) + (–2) = –10
حالا شما 10$ بدهکارید.
قوانین جبر: اگر علامتها یکسان باشند. شما ابتدا حاصل جمع را پیدا می کنید و سپس علامت را به همان شکل قرار می دهید. اگر a و b نماینده دو عدد حقیقی باشند، این قانون را می توان به شکل زیر نوشت:
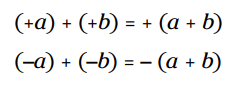
فرض کنید مشغول جمع زدن 3- و 2- هستید. علامت ها یکسان هستند. شما ابتدا حاصل جمع 3 و 2 را پیدا می کنید که 5 می شود. چون علامت اعداد منفی بوده است، پس علامت پاسخ نیز منفی خواهد شد.
در اینجا چند مثال دیگر داریم:
(+8) + (+11) = +19
(–14) + (–100) = –114
(+4) + (+7) + (+2) = +13
(–5) + (–2) + (–3) + (–1) = –11
همانطور که دیدید، جمع کردن اعداد دارای علامت یکسان کار بسیار آسانی بود.
جمع اعداد غیر هم علامت
آیا رابطه بین لئو (Leo) و جمینای (Gemini) به نتیجه می رسد؟ من پاسخ این سوال را نمی دانم، اما می دانم که جمع اعداد دارای علامت های متفاوت به نتیجه زیبایی می رسد. شما فقط کافیست چگونگی محاسبه را بدانید، و در این بخش من به شما می گویم.
قوانین جبر: وقتی که علامت دو عدد با یکدیگر متفاوت باشد، برای مدتی علامت آنها را فراموش کنید و اختلاف بین آن دو عدد را بدست آورید. در واقع این حاصل تفریق بین قدر مطلق آنها می باشد. عددی که از 0 دورتر باشد، علامت پاسخ را تعیین می کند.

ببینید هنگام جمع اعداد دارای علامت متفاوت چه اتفاقی می افتد:
-
شما 20$ در کیف پولتان دارید و 12$ از آن را برای خرید بلیط تئاتر هزینه می کنید:
(+20) + (–12) = +8
در حال حاضر شما 8$ دارید.
-
من 20$ دارم، اما برای پر کردن باک بنزین خودرو ام نیاز به 32$ دارم:
(+20) + (–32) = –12
من برای پر کردن باک بنزین مجبورم 12$ قرض بگیرم.
در اینجا چند مثال دیگر از پیدا کردن حاصل جمع اعداد دارای علامتهای متفاوت را می بینید:
(+6) + (–7) = –1اختلاف بین 6 و 7 عدد 1 می باشد. فاصله عدد 7 تا 0 در خط اعداد بیشتر از فاصله 6 تا 0 می باشد، و علامت 7 منفی می باشد، بنابراین علامت پاسخ نیز منفی خواهد بود.
(-6) + (+7) = +1این بار 7 مثبت می باشد. هنوز هم فاصله 7 نسبت به 6 از 0 بیشتر است. این بار علامت پاسخ مثبت می باشد.
(-4) + (+3) + (+7) + (-5) = +1اگر این عبارت را به ترتیب از سمت چپ به راست در نظر بگیرید (ضمن اینکه در عملیات جمع می توانید به دلخواه ترتیب را تغییر نیز بدهید)، ابتدا دو عدد اول را با یکدیگر جمع می کنید که حاصل 1- می شود. حاصل جمع 1- و 7+ می شود 6+. در نهایت حاصلجمع 6+ و 5- می شود 1+.
تفریق اعداد علامت دار
تفریق اعداد علامت دار واقعاً کار ساده ای می باشد: به جای اینکه یک مجموعه از قوانین جدید را برای تفریق اعداد علامت دار اختراع کنند، ریاضیدانان متوجه شدند که ساده تر اینست که مسائل تفریق را به مسائل جمع تبدیل کنند، و از قوانینی که برای جمع کردن وجود دارد استفاده کنند.
برای یک لحظه روش تفریق اعداد علامت دار را در نظر بگیرید. فقط مسأله تفریق را به یک مسأله جمع تبدیل کنید؟ زیاد معنادار به نظر نمی رسد؟ همه می دانند که شما نمی توانید فقط یک علامت عملیات حسابی را تغییر بدهید و انتظار داشته باشید که همان پاسخ یا پاسخ صحیح را بدست آورید. شما از خیلی وقت پیش می دانید که 4 - 10 با 4 + 10 یکسان نمی باشد. شما نمی توانید فقط عملیات را تغییر بدهید و انتظار پاسخ صحیح را هم داشته باشید.
خوب، برای اینکه روش بدرستی کار کند، شما در واقع دو چیز را تغییر می دهید. (تقریباً به نظر می رسد این مسأله جملۀ معروف "تکرار دو اشتباه منجر به یک کار درست نمی شوند" را باطل میکند، آیا اینطور نیست؟)
قوانین جبر: هنگام تفریق اعداد علامت دار، علامت منها را به یک علامت جمع تبدیل کنید و علامت عددی را که منها قبل از آن قرار داشت را به علامت متضاد علامت فعلی اش تبدیل کنید. سپس صرفاً با استفاده از قوانین جمع اعداد علامت دار، آن اعداد را با یکدیگر جمع کنید.
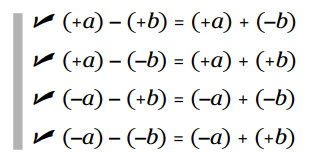
مثالهای زیر فرآیند تفریق اعداد علامت دار را در شرایط زندگی واقعی قرار می دهد:
-
زیردریایی 60 فوت زیر سطح آب بود که کاپیتان فریاد زد، "پایینتر!". زیردریایی 40 فوت پایینتر رفت:
–60 – (+40) = –60 + (–40) = –100
تفریق به جمع تغییر بدهید. عدد 40 را به متضاد آن یعنی 40- تغییر بدهید. سپس از قوانین جمع استفاده کنید. در حال حاضر زیردریایی 100 فوت زیر سطح دریا می باشد.
-
چندتا بچه تظاهر می کنند که در یک برنامه تلویزیونی واقعی هستند و به چند جای پا در دیوار مصنوعی کوه نوردی چسبیده اند. یک تیم موقعیت بازیکن تیم مقابل را به چالش می کشد. "شما قرار بود 3 فوت پایین بروید، سپس 8 فوت بالا بروید، سپس 4 فوت پایین بروید. شما نباید از موقعیتی که آغاز کردید 1 فوت بالاتر باشید!" داور تصمیم می گیرد تا با عقب بازگرداندن بازیکن - با حرکاتی معکوس - موضوع را بررسی کند. کاری کنید بازیکن حرکات معکوس انجام بدهد، یا حرکات را تفریق کنید:
–(–3) – (+8) – (–4) = +(+3) + (–8) + (+4) = –5 + (+4) = –1
بازیکن در نهایت با 1 فوت پایینتر از جای فعلی اش کار را به اتمام می رساند، بنابراین او در وهله اول به درستی حرکت کرده است.
در اینجا چند مثال از تفریق اعداد علامت دار داریم:
-
–16 – 4 = –16 + (–4) = –20
تفریق تبدیل به جمع می شود و 4+ تبدیل به منفی می گردد. سپس از آنجا که مشغول جمع دو عدد علامت دار با علامت یکسان هستید، طبق قاعده مجموع آن دو را پیدا می کنید و علامت مشترک آنها را به عنوان علامت پاسخ نیز قرار می دهید.
-
–3 – (–5) = –3 + (+5) = 2
تفریق تبدیل به جمع می شود و 5- نیز تبدیل به مثبت می گردد. هنگام جمع زدن اعداد دارای علامت متفاوت، اختلاف بین دو عدد را محاسبه می کنید. سپس علامت پاسخ یعنی 2 مثبت می شود، زیرا فاصله 5+ تا 0 بیشتر است.
-
9 – (–7) = 9 + (+7) = 16
تفریق تبدیل به جمع، و 7- تبدیل به مثبت می شود. هنگام جمع اعداد دارای علامت یکسان، حاصل جمع آنها را پیدا می کنید. از آنجا که هر دو عدد مثبت هستند، پاسخ نیز عددی مثبت خواهد بود.
ضرب و تقسیم اعداد علامت دار
ضرب و تقسیم اعداد علامت دار واقعاً ساده ترین کار ممکن می باشند. تا زمانی که شما بتوانید ضرب و تقسیم را انجام بدهید، قوانین نه تنها ساده هستند، بلکه در مورد هر دو عملیات یکسان می باشند.
بورس را در نظر بگیرید (چیزی که این روزها زیاد در نظر گرفته می شود). خبرنگار اعلام می کند "داو جونز" (Dow Jones) در یک ردیف دوبار 20 امتیاز پایین رفت. شما دو مرتبه 20- را در یک در یکدیگر ضرب می کنید تا 40- را به دست آورید. بنابراین حاصلضرب یک عدد منفی به تعداد دفعات مثبت، منفی می باشد.
در مورد تقسیم چطور؟ شما و سه تا از دوستانتان تصمیم می گیرید تا برای دوست دیگری ناهار بخرید. قیمت ناهار 23.64$ می باشد. هر نفر چقدر باید مشارکت کند؟ عدد 23.64- را بر 4 تقسیم کنید، و میزان مشارکت هر نفر 5.91- خواهد بود.
قوانین جبر: هنگامی که دو عدد علامت دار را ضرب یا تقسیم می کنید، اگر هر دو علامت یکسان باشند پاسخ مثبت خواهد بود. اگر دو علامت متفاوت باشند، پاسخ منفی خواهد بود.
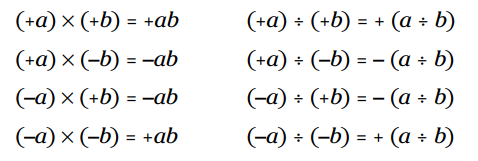
توجه کنید که در کدام موارد پاسخ مثبت و در کدام موارد پاسخ منفی می باشد. شما می بینید که هنگامی که یک عدد مثبت و یک عدد منفی داشته باشید، تفاوتی نمی کند که عدد منفی اول آمده باشد یا دوم. همچنین، توجه کنید که ضرب و تقسیم مانند همان ضرب و تقسیم همیشگی هستند و تفاوتی نمی کنند، فقط علامت ها در اینجا باید مورد توجه قرار بگیرند.
در اینجا چند مثال از ضرب و تقسیم اعداد علامت دار داریم:
در موقعی که چندین عدد را در یکدیگر ضرب یا تقسیم می کنید یا ترکیبی از چند ضرب و تقسیم را یکجا دارید، می توانید این عملیات ها را با استفاده از قوانین زوج-فرد زیر ترکیب کنید.
قوانین جبر: برطبق قانون زوج-فرد، هنگامی که یک دسته از اعداد را در یکدیگر ضرب یا تقسیم می کنید، تعداد علامت های منفی را بشمارید تا علامت پاسخ را تعیین کنید. اگر تعداد اعداد دارای علامت منفی یک تعداد زوج باشد، پاسخ مثبت خواهد بود. اگر هم این تعداد فرد باشد، پاسخ منفی خواهد بود.
در اینجا چند مثال از ضرب و تقسیم مجموعه ای از اعداد علامت دار را می بینید:
-
(+2) × (–3) × (+4) = –24
این مسأله فقط یک علامت منفی دارد. از آنجا که 1 عددی فرد می باشد (و البته تنهاترین عدد دنیا می باشد!)، پاسخ منفی خواهد بود. بخش های عددی (یعنی 2 و 3 و 4) در یکدیگر ضرب می شوند و علامت منفی به عنوان نشانه آن تعیین می شود.
-
(+2) × (–3) × (+4) × (–1) = +24
دو علامت منفی به معنای مثبت بودن پاسخ می باشد، زیرا 2 عددی زوج است.
-
یک تعداد زوج از اعداد منفی یعنی شما پاسخی مثبت خواهید داشت. یا، اگر می خواهید مسأله را در دو قسمت انجام بدهید، ابتدا اعداد موجود در صورت کسر را در یکدیگر ضرب کنید تا به پاسخ 12- برسید. سپس شما یک عدد منفی خواهید داشت که بر عدد منفی دیگری تقسیم می شود، که پاسخش مثبت می شود. واقعاً ساده تر اینست که فقط تعداد علامت های منفی را بشمارید و بر اساس قانون زوج-فرد علامت پاسخ را تعیین کنید.
-
حاصل سه عدد منفی، یک منفی است.
-
(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1) = –1
یک تعداد فرد از منفی ها به شما علامت منفی می دهد. و اگر در اینجا فقط یک (1-) بیشتر می داشتیم، پاسخ مثبت می بود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: