خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ویژگی جابجایی پذیری و ویژگی شرکت پذیری

عملیات های جبر قوانین خاصی را دنبال می کنند، و آن قوانین چندین ویژگی دارند. ویژگی ها معمولاً محاسبات را ساده تر می کنند. در این بخش، در مورد دو تا از این ویژگی ها صحبت می کنم - ویژگی جابجایی پذیری (commutative property) و ویژگی شرکت پذیری (associative property).

قبل از اینکه در مورد ویژگی جابجایی پذیری (commutative property) بحث کنیم، نگاهی به کلمه commute (رفت و آمد) بیندازیم. شما احتمالاً به مدرسه یا محل کار می روید و می دانید که اگر از منزل به محل کار بروید یا برعکس، از محل کار به منزل برگردید، فاصله یکسان خواهد بود: مسافت تغییری نمی کند زیرا شما فقط جهت را تغییر داده اید (البته در هنگام رفت و آمد در ساعت شلوغی ممکن است به نظر برسد مسافت بیشتر شده است!).
قاعده یکسانی در برخی ازعملیات های جبری برقرار است: به عنوان مثال حاصل جمع 1 و 2 در هر دو حالت زیر یکسان می باشد و ترتیب چینش در نتیجه تغییری ایجاد نمی کند:
نگاهی به چگونگی عملکرد ویژگی جابجایی پذیری بیندازید:
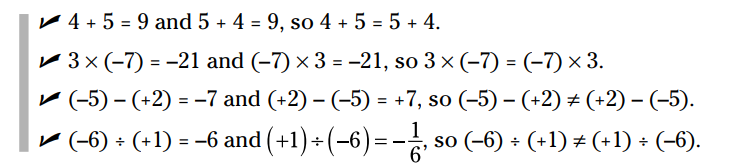
وقتی یک عملیات را انجام می دهید، ویژگی جابجایی پذیری با ترتیب اعداد سر و کار دارد. وقتی عملیاتهایی را بر روی بیش از دو عدد انجام می دهید ویژگی شرکت پذیری (associative property) با چگونگی گروه بندی اعداد، سر و کار دارد.
در مورد اینکه کلمه associate (پیوستن) چه معنایی می دهد، فکر کنید. هنگامی که به شخصی می پیوندید، به آن شخص نزدیک هستید، یا با آن شخص در یک گروه مشترک هستید. فرض کنید آنیکا (Anika)، بکی (Becky)، و کورا (Cora) به هم پیوسته اند. خواه اینکه آنیکا رانندگی کند و بکی را سوار کند و هر دوی آنها دنبال کورا بروند و او را سوار کنند، یا اینکه کورا در خانه بکی باشد و آنیکا هر دوی آنها را همزمان سوار کند، نتیجه یکسانی حاصل می شود - در نهایت هر سه بانو الآن سوار ماشین هستند.
در اینجا چگونگی کارکرد ویژگی شرکت پذیری را می بینید:
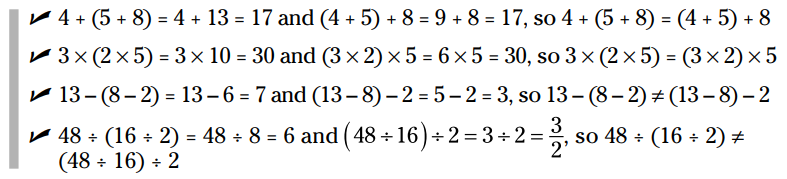
ویژگیهای جابجایی پذیری و شرکت پذیری در هنگام کار با عبارتهای جبری ابزارهای سودمندی در دست شما هستند. شما می توانید ترتیب برخی اعداد را تغییر بدهید یا گروه بندی آنها را تغییر بدهید تا کار شسته و رفته تر یا راحتتر گردد. فقط یادتان باشد که شما می توانید ویژگی جابجایی پذیری و شرکت پذیری را در مورد جمع و ضرب استفاده کنید و نه تفریق و تقسیم.
شما می توانید با استفاده از ویژگی های جابجایی پذیری و شرکت پذیری پاسخ مسأله زیر را پیدا کنید:
حالا با استفاده از ویژگی شرکت پذیری گروه بندیهایی را به شکل زیر ایجاد کنید:

ویژگی جابجایی پذیری (commutative property)
قبل از اینکه در مورد ویژگی جابجایی پذیری (commutative property) بحث کنیم، نگاهی به کلمه commute (رفت و آمد) بیندازیم. شما احتمالاً به مدرسه یا محل کار می روید و می دانید که اگر از منزل به محل کار بروید یا برعکس، از محل کار به منزل برگردید، فاصله یکسان خواهد بود: مسافت تغییری نمی کند زیرا شما فقط جهت را تغییر داده اید (البته در هنگام رفت و آمد در ساعت شلوغی ممکن است به نظر برسد مسافت بیشتر شده است!).
قاعده یکسانی در برخی ازعملیات های جبری برقرار است: به عنوان مثال حاصل جمع 1 و 2 در هر دو حالت زیر یکسان می باشد و ترتیب چینش در نتیجه تغییری ایجاد نمی کند:
1 + 2 = 3به همین ترتیب، حاصلضرب 2 و 3 نیز با تغییر ترتیب عملیات یکسان باقی می ماند:
2 + 1 = 3
2 x 3 = 6
3 x 2 = 6
قوانین جبر: ویژگی جابجایی پذیری به این معنا می باشد که می توانید در یک عملیات ترتیب اعداد را بدون اینکه در نتیجه عملیات تاثیری داشته باشد، تغییر بدهید. جمع و ضرب جابجایی پذیر می باشند. تفریق و تقسیم جابجایی پذیر نمی باشند، بنابراین:
a + b = b + a
a × b = b × a
a – b ≠ b – a (except in a few special cases)
a ÷ b ≠ b ÷ a (except in a few special cases)
نکات فنی: به طور کلی، تفریق و تقسیم جابجایی پذیر نمی باشند. موارد خاصی هم هستند که اگر اعداد مشخصی را با دقت انتخاب کنید این اتفاق می افتد. برای مثال، اگر a و b هر دو اعداد یکسانی باشند، در این مورد تفریق جابجایی پذیر خواهد بود، زیرا تغییر دادن ترتیب a و b نتیجه را تغییر نمی دهد. در مورد تقسیم، اگر a و b دو عدد مخالف هم باشند، نتیجه 1- خواهد شد و تفاوتی هم نمی کند با چه ترتیبی آنها را بر یکدیگر تقسیم کنید. ضمناً، به همین دلیل هم هست که در ریاضی اثبات ها (proofs) بسیار مهمند. چند مورد خاص از چیزی ممکن است درست کار کند، اما یک قانون واقعی یا تئوری باید همیشه به درستی کار کند.
نگاهی به چگونگی عملکرد ویژگی جابجایی پذیری بیندازید:
ویژگی شرکت پذیری (associative property)
وقتی یک عملیات را انجام می دهید، ویژگی جابجایی پذیری با ترتیب اعداد سر و کار دارد. وقتی عملیاتهایی را بر روی بیش از دو عدد انجام می دهید ویژگی شرکت پذیری (associative property) با چگونگی گروه بندی اعداد، سر و کار دارد.
در مورد اینکه کلمه associate (پیوستن) چه معنایی می دهد، فکر کنید. هنگامی که به شخصی می پیوندید، به آن شخص نزدیک هستید، یا با آن شخص در یک گروه مشترک هستید. فرض کنید آنیکا (Anika)، بکی (Becky)، و کورا (Cora) به هم پیوسته اند. خواه اینکه آنیکا رانندگی کند و بکی را سوار کند و هر دوی آنها دنبال کورا بروند و او را سوار کنند، یا اینکه کورا در خانه بکی باشد و آنیکا هر دوی آنها را همزمان سوار کند، نتیجه یکسانی حاصل می شود - در نهایت هر سه بانو الآن سوار ماشین هستند.
قوانین جبر: ویژگی شرکت پذیری به این معنا می باشد که حتی اگر گروه بندی عملیاتی تغییر کند، نتیجه یکسان باقی بماند. (اگر در مورد خود مفهوم گروه بندی نیاز به یک یادآوری دارید، فصل 1 را مرور کنید.) عملیات جمع و ضرب شرکت پذیر هستند. عملیات تفریق و تقسیم شراکت پذیر نیستند. بنابراین:
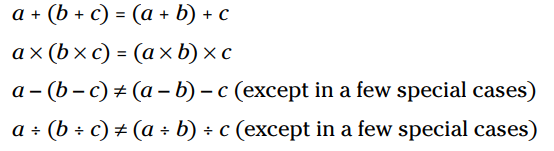
نکات فنی: شما ممکن است بتوانید موارد خاصی را پیدا کنید که برخلاف انتظار ویژگی شرکت پذیری در مورد تفریق یا تقسیم نیز به درستی کار کند. برای مثال به موارد زیر دقت کنید:
5 – (4 – 0) = (5 – 4) – 0با این وجود این موارد استثناء هستند و نمی توان تعمیمشان داد، یک قانون باید همیشه به درستی کار کند.
6 ÷ (3 ÷ 1) = (6 ÷ 3) ÷ 1
در اینجا چگونگی کارکرد ویژگی شرکت پذیری را می بینید:
ویژگیهای جابجایی پذیری و شرکت پذیری در هنگام کار با عبارتهای جبری ابزارهای سودمندی در دست شما هستند. شما می توانید ترتیب برخی اعداد را تغییر بدهید یا گروه بندی آنها را تغییر بدهید تا کار شسته و رفته تر یا راحتتر گردد. فقط یادتان باشد که شما می توانید ویژگی جابجایی پذیری و شرکت پذیری را در مورد جمع و ضرب استفاده کنید و نه تفریق و تقسیم.
شما می توانید با استفاده از ویژگی های جابجایی پذیری و شرکت پذیری پاسخ مسأله زیر را پیدا کنید:
417 + 932 + (– 416) + (– 432) + 800برای ساده سازی این عبارت، در حالت معمول شما از سمت چپ به راست حرکت می کنید، و به ترتیب جمع و تفریقها را انجام می دهید، اما بازچینش عبارت می تواند کار را بهتر کند. با استفاده از ویژگی جابجایی پذیری جای 932 و 416- را تعویض کنید:
417 + (–416) + 932 + (–432) + 800
حالا با استفاده از ویژگی شرکت پذیری گروه بندیهایی را به شکل زیر ایجاد کنید:
(417 + [–416]) + (932 + [–432]) + 800 = 1 + 500 + 800 = 1,301همانطور که خودتان هم دیدید، در این مثال ما با استفاده از ویژگی های جابجایی پذیری و شرکت پذیری یک مسأله را که به ظاهر برای حلش نیاز به ماشین حساب داشتیم، به شکلی در آوردیم که به صورت کاملاً ذهنی و به سادگی قابل حل باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: