خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اعداد اعشاری (Decimals)
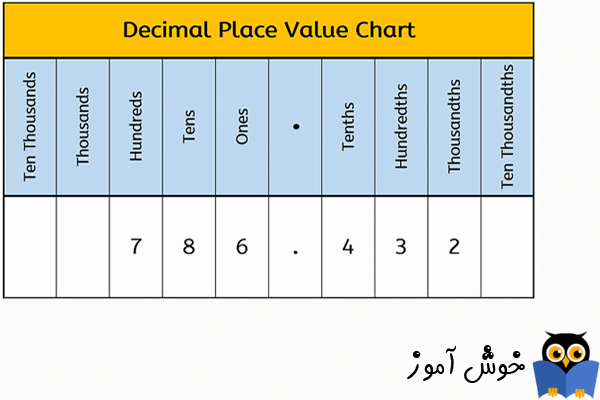
اعداد اعشاری (Decimals) چیزی به جز کسرهای شکوهمند نیستند. اعداد اعشاری به این دلیل خاص هستند که وقتی آنها را به شکل کسر بنویسید، مخرج آنها همیشه مضربی از 10 می باشد - برای مثال، 10، 100، 1000، و به همین ترتیب. از آنجا که اعداد اعشاری کسرهایی بدین شکل خاص هستند، شما حتی لازم نیست خودتان را با قسمت مخرج اذیت کنید. فقط صورت کسر را بنویسید و از یک ممیز اعشاری (decimal point) استفاده کنید تا نشان دهید این یک کسر است که مخرج آن مضربی از 10 می باشد.

در اینجا چند مثال از تبدیل اعداد اعشاری به کسرها را می بینید:
کسرهای اعشاری عالی هستند، زیرا شما می توانید آنها را به سادگی جمع، تفریق، ضرب، و تقسیم کنید. سادگی در محاسبه و سادگی در نگارش، از دلایلی هستند که تبدیل یک کسر به یک عدد اعشاری را کار مطلوبی می کند.
تمامی کسرها می توانند به اعداد اعشاری تبدیل شوند. در فصل 1 به شما گفتم، اعداد گویا (rational numbers) ارقام اعشاری دارند که می توانند دقیقاً به صورت کسر نوشته شوند. قسمت اعشاری یک عدد گویا به شکلی است که یا ارقام اعشارش جایی خاتمه می یابد و یا اینکه با یک الگوی تکراری تا ابد ادامه پیدا می کند.
برای تبدیل یک کسر به یک عدد اعشاری، فقط صورت آن را بر مخرج آن تقسیم کنید:

در تقسیم 4 بر 11، تقسیم هرگز خاتمه نمی یابد، برای همین علامت سه نقطه در سمت راست عدد اعشاری ...0.363636 نشان می دهد که این الگو تا ابد ادامه پیدا خواهد کرد.
اگر تقسیم به صورت برابر صورت نپذیرد، شما می توانید ارقام تکرار شونده را نشان دهید یا می توانید بعد از چند رقم اعشار، تقسیم را متوقف کنید و آن را گرد کنید.
برای گرد کردن اعداد:
مثال: در اینجا چند مثال از گرد کردن هر عدد اعشاری به نزدیکترین "یک هزارم" (سه رقم اعشار) می بینید:
اعداد اعشاری، اعداد گویا را نمایش می دهند و دارای دو نوع هستند: اعداد اعشاری مختوم (terminating decimals) و اعداد اعشاری متناوب (repeating decimals). هنگام تبدیل اعداد اعشاری به کسرها، ارقام اعشار را بالای چندرقم دیگر قرار می دهید و کسر را کاهش می دهید.
مثال: عدد 0.36 را به یک کسر تبدیل کنید:
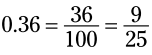
در عدد 36 دو رقم وجود دارد، بنابراین بعد از عدد 1 که در مخرج قرار می گیرد دو صفر می گذاریم. از آنجا که هر دو عدد 36 و 100 بر 4 بخش پذیرند، کسر را کاهش می دهیم.
مثال: عدد 0.403 را به یک کسر تبدیل کنید:
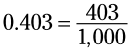
در عدد 403 سه رقم وجود دارد، بنابراین بعد از 1 در مخرج کسر تعداد سه صفر قرار می دهیم. این کسر کاهش نمی یابد.
مثال: عدد 0.0005 را به یک کسر تبدیل کنید:
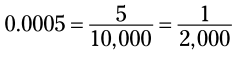
فراموش نکنید که تعداد صفرهای قبل از 5 را نیز در شمارش ارقام اعشار لحاظ کنید. این کسر کاهش می یابد.
هنگامی که یک عدد اعشاری خودش را مدام تکرار می کند، شما همیشه می توانید کسر معادل آن عدد اعشاری را بیابید.
در اینجا چند مثال از تبدیل اعداد اعشاری تکرار شونده به کسرها را داریم:

یادتان باشد: تعداد ارقام سمت راست ممیز اعشاری (ارقام اعشاری) در یک عدد به شما می گوید تعداد صفرهای مضربی از 10 که در کسر معادل این عدد اعشاری نوشته می شود، چندتا می باشد.
در اینجا چند مثال از تبدیل اعداد اعشاری به کسرها را می بینید:
-
: عدد اعشاری فقط یک رقم (3) در سمت راست ممیز اعشاری دارد، بنابراین مخرج کسر یک 0 دارد.
-
: عدد اعشاری سه رقم (408) در سمت راست ممیز اعشاری دارد، بنابراین شما می توانید مضربی از 10 با سه صفر را استفاده کنید.
-
: عدد اعشاری پنج رقم (00009) در سمت راست ممیز اعشاری دارد. عدد 60 در برابر کسر نوشته می شود و در مقدار اعشاری تاثیری ندارد. در هنگام تبدیل اعشار به کسر، صفرهای قبل از عدد (lead zeros) در صورت کسر، در مقابل 9 نوشته نمی شوند. شما با اولین عدد غیر از صفر نوشتن صورت کسر را آغاز می کنید.
نکات فنی: یک رقم (digit) هر عدد تنها از 0 تا 9 می باشد. (اما، هنگامی که ده رقم را با انگشتان دستتان شمارش می کنید، با 1 آغاز می کنید و با 10 شمارش را خاتمه می دهید.)
کسرهای اعشاری عالی هستند، زیرا شما می توانید آنها را به سادگی جمع، تفریق، ضرب، و تقسیم کنید. سادگی در محاسبه و سادگی در نگارش، از دلایلی هستند که تبدیل یک کسر به یک عدد اعشاری را کار مطلوبی می کند.
تبدیل کسرها به اعداد اعشاری
تمامی کسرها می توانند به اعداد اعشاری تبدیل شوند. در فصل 1 به شما گفتم، اعداد گویا (rational numbers) ارقام اعشاری دارند که می توانند دقیقاً به صورت کسر نوشته شوند. قسمت اعشاری یک عدد گویا به شکلی است که یا ارقام اعشارش جایی خاتمه می یابد و یا اینکه با یک الگوی تکراری تا ابد ادامه پیدا می کند.
برای تبدیل یک کسر به یک عدد اعشاری، فقط صورت آن را بر مخرج آن تقسیم کنید:
در تقسیم 4 بر 11، تقسیم هرگز خاتمه نمی یابد، برای همین علامت سه نقطه در سمت راست عدد اعشاری ...0.363636 نشان می دهد که این الگو تا ابد ادامه پیدا خواهد کرد.
اگر تقسیم به صورت برابر صورت نپذیرد، شما می توانید ارقام تکرار شونده را نشان دهید یا می توانید بعد از چند رقم اعشار، تقسیم را متوقف کنید و آن را گرد کنید.
برای گرد کردن اعداد:
-
تعداد ارقام اعشاری را که می خواهید مشخص کنید و یک رقم بعد از آن در سمت راست را ببنید.
-
اگر آن یک رقم بیشتر برابر با 5 یا بیشتر باشد، آخرین رقمی را که می خواهید یک واحد افزایش بدهید.
-
اگر یک رقم بیشتر کوچکتر از 5 باشد، آخرین رقمی را که می خواهید بدون تغییر باقی بگذارید.
یادتان باشد: نماد ≈ به معنای "تقریباً برابر است با" (approximately equal) می باشد. این نماد در هنگامیکه اعداد را گرد می کنید، مفید خواهد بود.
مثال: در اینجا چند مثال از گرد کردن هر عدد اعشاری به نزدیکترین "یک هزارم" (سه رقم اعشار) می بینید:
-
: هنگامیکه می خواهید تا سه رقم اعشار گرد کردن را انجام بدهید، به رقم چهارم نگاه کنید (یک رقم بیشتر از آنچه می خواهید). رقم چهارم 6 می باشد، که بزرگتر از 5 است، بنابراین شما رقم سوم را 1 واحد افزایش می دهید، یعنی 3 را تبدیل به 4 می کنید.
-
: هنگامی که گرد کردن را تا سه رقم اعشار انجام می دهید، به رقم چهارم نگاه می کنید. رقم چهارم 2 می باشد، که کوچکتر از 5 است، بنابراین رقم سوم را بدون تغییر باقی می گذارید.
-
: هنگام گرد کردن اعداد تا سه رقم اعشار، به رقم چهارم نگاه کنید. رقم چهارم 5 می باشد، بنابراین رقم سوم را یک واحد افزایش می دهید، و 2 تبدیل به 3 می شود.
نکات فنی: شما ممکن است متوجه شوید برخی از افراد از یک قانون تناوب (alternate rule) برای گرد کردن در هنگامیکه یک رقم 5 را حذف می کنند، استفاده می کنند. قانون تناوب اینست که: به عدد زوج (even number) گرد کن. بنابراین اگر مشغول گرد کردن یک عدد تا سه رقم اعشار هستید، عدد 0.3125 به 0.312 گرد می شود (به سمت پایین و نزدیکترین عدد زوج)، و عدد 0.6175 به 0.618 گرد می شود (به سمت بالا و نزدیکترین عدد زوج).
تبدیل اعداد اعشاری به کسرها
اعداد اعشاری، اعداد گویا را نمایش می دهند و دارای دو نوع هستند: اعداد اعشاری مختوم (terminating decimals) و اعداد اعشاری متناوب (repeating decimals). هنگام تبدیل اعداد اعشاری به کسرها، ارقام اعشار را بالای چندرقم دیگر قرار می دهید و کسر را کاهش می دهید.
اعداد اعشاری مختوم (terminating decimals)
قوانین جبر: برای تبدیل یک عدد اعشاری مختوم به یک کسر، ارقام سمت راست ممیز اعشاری را در صورت کسر قرار دهید. عدد 1 را در مخرج کسر قرار بدهید و به تعداد ارقام اعشار بعد از آن صفر قرار بدهید. اگر لازم باشد کسر را کاهش بدهید.
مثال: عدد 0.36 را به یک کسر تبدیل کنید:
در عدد 36 دو رقم وجود دارد، بنابراین بعد از عدد 1 که در مخرج قرار می گیرد دو صفر می گذاریم. از آنجا که هر دو عدد 36 و 100 بر 4 بخش پذیرند، کسر را کاهش می دهیم.
مثال: عدد 0.403 را به یک کسر تبدیل کنید:
در عدد 403 سه رقم وجود دارد، بنابراین بعد از 1 در مخرج کسر تعداد سه صفر قرار می دهیم. این کسر کاهش نمی یابد.
مثال: عدد 0.0005 را به یک کسر تبدیل کنید:
فراموش نکنید که تعداد صفرهای قبل از 5 را نیز در شمارش ارقام اعشار لحاظ کنید. این کسر کاهش می یابد.
اعداد اعشاری متناوب یا اعداد اعشاری تکرار شونده (repeating decimals)
هنگامی که یک عدد اعشاری خودش را مدام تکرار می کند، شما همیشه می توانید کسر معادل آن عدد اعشاری را بیابید.
قوانین جبر: برای تبدیل یک عدد اعشاری تکرار شونده (که در آن هر رقمی بخشی از الگوی تکرار می باشد) به کسر متناظر آن، قسمت تکراری را در صورت کسر بنویسید. در مخرج کسر به تعداد ارقام اعشار عدد 9 را قرار دهید. اگر لازم باشد، کسر را ساده کنید.
در اینجا چند مثال از تبدیل اعداد اعشاری تکرار شونده به کسرها را داریم:
-
: سه رقم تکرار شونده 126 هستند. عدد 126 را در صورت کسر و سه عدد 9 در مخرج کسر قرار دهید. شما می توانید صورت و مخرج کسر را بر 9 تقسیم کرده و کسر را ساده کنید.
-
: شش رقم تکرار شونده در قسمت اعشار را در صورت کسر و شش رقم 9 در مخرج کسر قرار دهید. کاهش این کسر نیاز به چندین تقسیم دارد. فاکتورهای مشترک صورت و مخرج کسر 11، 13، 27، و 37 می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: