خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توان ها (Exponents)
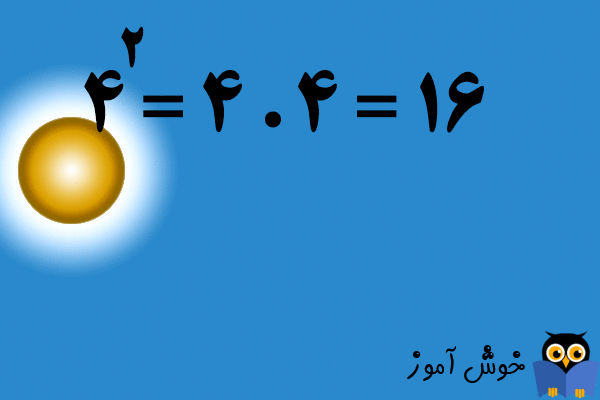
توان ها (Exponents)، آن نمادهای کوچک، اندکی بالاتر و در سمت راست اعداد، زمانی ایجاد شدند که ریاضیدانان تمایلی نداشتند مجبور به تکرار مداوم یک چیز باشند! توان چیست؟ توان یک عدد کوچک است که به صورت بالا نویس در گوشه بالا و سمت راست عددی بزرگتر که به آن پایه توان (base) گفته می شود، نوشته می شود، و به شما می گوید عدد بزرگتر چند مرتبه در خودش ضرب می شود. سه به توان چهار (34) یعنی 3 در خودش 4 مرتبه ضرب شود. موضوع را گرفتید؟ حالا به سراغ آن چیزی که اتفاق می افتد می رویم:

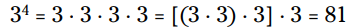
بنابراین، در واقع، سه به توان چهار (34) روش دیگری برای گفتن 81 می باشد.
وقتی جبر برای اولین بار - به جای استفاده از کلمات - با نمادها (symbols) نوشته شد، توان ها وجود نداشتند. اگر شما می خواستید متغیر y را شش مرتبه در خودش ضرب کنید، باید آن را به این شکل می نوشتید: yyyyyy. شبیه اینکه بخواهید با یک بچه سه ساله صحبت کنید: “Why, why, why, why, why, why” نوشتن یک متغیر (حرف الفبایی که نماینده اعداد می باشد) دوباره و دوباره و دوباره خسته کننده بود (درست مثل یک بچه سه ساله)، بنابراین سیستم فوق العاده توان ها ایجاد شد.
نوشتن اعداد با توان ها یک چیز است - دانستن اینکه معنای این توان ها چیست و شما با آن چه کارهایی می توانید بکنید، چیز دیگریست. استفاده از توان ها بسیار راحت است و به همین دلیل به زمان و زحمتی که برای فهمیدن قوانین استفاده از آنها می گذارید، می ارزد.
پایه یک عبارت توان دار می تواند هر عدد حقیقی (real number) باشد. (اعداد حقیقی، ترکیب اعداد گویا و اعداد گنگ می باشند.) خود توان نیز می تواند هر عدد حقیقی باشد. یک توان می تواند عددی مثبت، عددی منفی، عددی کسری، و یا حتی یک رادیکال باشد.
در اینجا چند مثال از استفاده نماد توان می بینید:
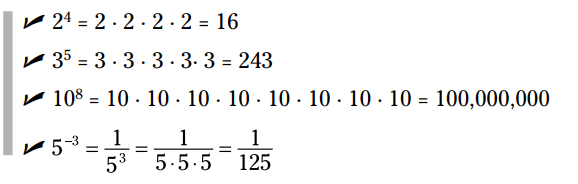
همانطور که می بینید، در مثال آخر عدد 5 به توان یک عدد منفی رسیده است. در مورد توان منفی در همین فصل آموزشهای لازم را ارائه می کنیم.
چیز زیبا در مورد توانهای 10 اینست که به شما می گوید چند تا صفر در پاسخ وجود دارد.
مثال: عبارت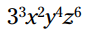 را بدون نمادهای توان بنویسید.
را بدون نمادهای توان بنویسید.
در این مثال، چندین پایه (base) در یکدیگر ضرب شده اند. هر پایه توان جداگانه خودش را دارد. متغیرهای x و y و z نماینده اعداد حقیقی هستند:
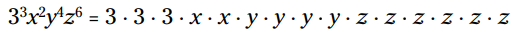
در همین مثال شما می توانید دلیل اینکه استفاده از توان ها ترجیح داده شده اند را به وضوح ببینید. و در مثال بعدی پایه توان یک دوجمله ای (binomial) می باشد.
مثال: عبارت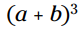 را بدون توان بنویسید.
را بدون توان بنویسید.
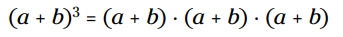
هنگامی که از توان ها استفاده می کنید، مقایسه مقادیر ساده تر است. سعی کنید این دو عدد را با یکدیگر مقایسه کنید 943,260,000,000,000,000,000,000 و 8,720,000,000,000,000,000,000,000 . کدامیک بزرگتر است؟ عدد اول ممکن است بزرگتر به نظر برسد، زیرا سه رقم اول آن به ظاهر بزرگتر از عدد دوم است. اما این فریب دهنده است. برای مقایسه اعداد بزرگ، آنها را به شکل حاصلضرب هایی که شامل توان باشند، بازنویسی کنید.
اعداد پیشین را می توانید به شکل زیر بازنویسی کنید:
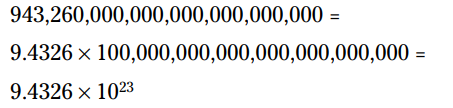
و
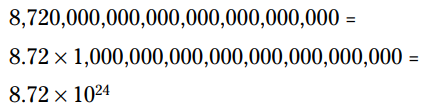
عددی که توان 10 آن بزرگتر باشد، عدد بزرگتر می باشد:
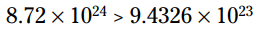
اگر توان ها برابر باشند، سپس اعدادی را که در توان 10 ضرب می شوند با یکدیگر مقایسه کنید.
چرا عددی که توان 10 آن بیشتر است، عدد بزرگتر است؟ به این دو عدد زیر که اندکی بیشتر قابل مدیریت هستند نگاهی بیندازید (آنها بیش از 20 صفر ندارند!):
مثال: ستاره رایجل (Rigel) که در صورت فلکی اوراین (constellation Orion) قرار دارد، 777 سال نوری با زمین فاصله دارد. یک سال نوری (light year) مسافتی است که نور در طول یک سال طی می کند. بنابراین، اگر نور با سرعت 186,000 مایل در ثانیه (miles per second) حرکت کند: شما 186,000 را در 60 ثانیه که در دقیقه وجود دارد ضرب می کنید، سپس در 60 دقیقه هر ساعت و سپس در 24 ساعت هر روز و سپس در 365 روز یک سال و سپس در 777 سال ضرب می کنید تا به عدد تقریبی 4,557,645,792,000,000 مایل برسید. اگر این مقدار را به شکل توان دار بنویسیم، فاصله زمین تا ستاره رایجل به شکل زیر می باشد:
مثال: ویروس ها کوچکترین میکروبها هستند، با این وجود یک ویران کننده کثیف هستند! ویروس ابولا (Ebola) به اندازه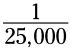 اینچ، یا 0.00004 اینچ (inch) می باشد. ویروس آنفلوآنزا (influenza) به اندازه
اینچ، یا 0.00004 اینچ (inch) می باشد. ویروس آنفلوآنزا (influenza) به اندازه 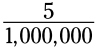 اینچ یا 0.000005 اینچ می باشد. در نماد علمی (scientific notation) این دو ویروس به شکل زیر نشان داده می شوند:
اینچ یا 0.000005 اینچ می باشد. در نماد علمی (scientific notation) این دو ویروس به شکل زیر نشان داده می شوند:
هنگامی که مردم دربارۀ فاصله بین سیاره ها، تعداد دانه های شن، یا مجموع مبلغی که توسط دولت خرج می شود، صحبت می کنند، آنها مجبورند از اعداد خیلی بزرگی استفاده کنند. هنگامی که موضوع بحث به اندازه گیری سلولهای گیاهان یا حیوانات، اندازۀ اتمها، یا سایر چیزهای کوچک اینچنینی، تبدیل شود، مردم از اعداد خیلی کوچک استفاده می کنند. نماد علمی (Scientific notation) یک روش استاندارد برای ثبت کردن این اعداد خیلی کوچک و خیلی بزرگ می باشد، تا آنها در یک خط از یک کتاب جا شوند و همینطور به آسانی با یکدیگر قابل مقایسه باشند. همچنین انجام محاسبات اعداد خیلی بزرگ یا خیلی کوچک، در شکل نماد علمی، بسیار ساده تر می باشد.
شما می توانید اعداد بزرگ و کوچک را در نماد علمی بنویسید، به این شکل که ممیز اعشاری را به نحوی حرکت بدهید که عددی بین 1 تا 10 بسازید، و سپس مشخص سازید، ممیز اعشاری چند خانه حرکت کرده است و عدد 10 را به توانِ تعداد حرکتهای ممیز اعشاری برسانید. اینکه توان 10 مثبت یا منفی باشد، بستگی به این دارد که ممیز اعشاری به سمت راست یا چپ حرکت کرده باشد: حرکت ممیز اعشاری به سمت راست توان را منفی می سازد، حرکت ممیز اعشاری به سمت چپ توان را مثبت می سازد.
برای نوشتن یک عدد در نماد علمی:
مثال: در اینجا چند عدد را که با نماد علمی نوشته شده اند، می بینید:

بنابراین، در واقع، سه به توان چهار (34) روش دیگری برای گفتن 81 می باشد.
ضرب یک چیز یکسان، دوباره و دوباره و دوباره
وقتی جبر برای اولین بار - به جای استفاده از کلمات - با نمادها (symbols) نوشته شد، توان ها وجود نداشتند. اگر شما می خواستید متغیر y را شش مرتبه در خودش ضرب کنید، باید آن را به این شکل می نوشتید: yyyyyy. شبیه اینکه بخواهید با یک بچه سه ساله صحبت کنید: “Why, why, why, why, why, why” نوشتن یک متغیر (حرف الفبایی که نماینده اعداد می باشد) دوباره و دوباره و دوباره خسته کننده بود (درست مثل یک بچه سه ساله)، بنابراین سیستم فوق العاده توان ها ایجاد شد.
نماد توان
نوشتن اعداد با توان ها یک چیز است - دانستن اینکه معنای این توان ها چیست و شما با آن چه کارهایی می توانید بکنید، چیز دیگریست. استفاده از توان ها بسیار راحت است و به همین دلیل به زمان و زحمتی که برای فهمیدن قوانین استفاده از آنها می گذارید، می ارزد.
پایه یک عبارت توان دار می تواند هر عدد حقیقی (real number) باشد. (اعداد حقیقی، ترکیب اعداد گویا و اعداد گنگ می باشند.) خود توان نیز می تواند هر عدد حقیقی باشد. یک توان می تواند عددی مثبت، عددی منفی، عددی کسری، و یا حتی یک رادیکال باشد.
قوانین جبر: هنگامی که یک عدد x به تعداد n مرتبه در خودش ضرب شود، در اینجا عدد n به شکل زیر می تواند تعداد دفعات ضرب شدن x در خودش را توصیف کند:
xn = x · x · x · x · x . . . n مرتبه
هشدار: با وجود اینکه در عبارت xn متغیر x می تواند هر عدد حقیقی باشد و n نیز می تواند هر عدد حقیقی باشد، هر دوی آنها همزمان نمی توانند 0 باشند. برای مثال 00 در واقعیت هیچ معنایی در جبر ندارد. برای اثبات دلیل وجود این محدودیت نیاز به دوره آموزشی حساب دیفرانسیل و انتگرال (calculus) می باشد. همچنین محدودیت دیگر اینست که اگر x برابر با 0 باشد، سپس n نمی تواند عددی منفی باشد.
در اینجا چند مثال از استفاده نماد توان می بینید:
همانطور که می بینید، در مثال آخر عدد 5 به توان یک عدد منفی رسیده است. در مورد توان منفی در همین فصل آموزشهای لازم را ارائه می کنیم.
چیز زیبا در مورد توانهای 10 اینست که به شما می گوید چند تا صفر در پاسخ وجود دارد.
مثال: عبارت
در این مثال، چندین پایه (base) در یکدیگر ضرب شده اند. هر پایه توان جداگانه خودش را دارد. متغیرهای x و y و z نماینده اعداد حقیقی هستند:
در همین مثال شما می توانید دلیل اینکه استفاده از توان ها ترجیح داده شده اند را به وضوح ببینید. و در مثال بعدی پایه توان یک دوجمله ای (binomial) می باشد.
مثال: عبارت
نکته: پرانتزها به این معنا می باشند که شما ابتدا باید دو مقدار داخل پرانتز را با یکدیگر جمع کنید و سپس آنها را به توان برسانید.
مقایسه با توان ها
هنگامی که از توان ها استفاده می کنید، مقایسه مقادیر ساده تر است. سعی کنید این دو عدد را با یکدیگر مقایسه کنید 943,260,000,000,000,000,000,000 و 8,720,000,000,000,000,000,000,000 . کدامیک بزرگتر است؟ عدد اول ممکن است بزرگتر به نظر برسد، زیرا سه رقم اول آن به ظاهر بزرگتر از عدد دوم است. اما این فریب دهنده است. برای مقایسه اعداد بزرگ، آنها را به شکل حاصلضرب هایی که شامل توان باشند، بازنویسی کنید.
اعداد پیشین را می توانید به شکل زیر بازنویسی کنید:
و
عددی که توان 10 آن بزرگتر باشد، عدد بزرگتر می باشد:
اگر توان ها برابر باشند، سپس اعدادی را که در توان 10 ضرب می شوند با یکدیگر مقایسه کنید.
چرا عددی که توان 10 آن بیشتر است، عدد بزرگتر است؟ به این دو عدد زیر که اندکی بیشتر قابل مدیریت هستند نگاهی بیندازید (آنها بیش از 20 صفر ندارند!):
3 × 102 9 × 101در واقع این اعداد با حذف توان به شکل زیر در می آیند:
3 × 100 = 300با وجودیکه 9 از 3 بزرگتر می باشد، این توان بیشتر 10 می باشد که برنده مسابقه است.
9 × 10 = 90
مثال: ستاره رایجل (Rigel) که در صورت فلکی اوراین (constellation Orion) قرار دارد، 777 سال نوری با زمین فاصله دارد. یک سال نوری (light year) مسافتی است که نور در طول یک سال طی می کند. بنابراین، اگر نور با سرعت 186,000 مایل در ثانیه (miles per second) حرکت کند: شما 186,000 را در 60 ثانیه که در دقیقه وجود دارد ضرب می کنید، سپس در 60 دقیقه هر ساعت و سپس در 24 ساعت هر روز و سپس در 365 روز یک سال و سپس در 777 سال ضرب می کنید تا به عدد تقریبی 4,557,645,792,000,000 مایل برسید. اگر این مقدار را به شکل توان دار بنویسیم، فاصله زمین تا ستاره رایجل به شکل زیر می باشد:
4,557,645,792,000,000 ≈ 4.558 × 1015
مثال: ویروس ها کوچکترین میکروبها هستند، با این وجود یک ویران کننده کثیف هستند! ویروس ابولا (Ebola) به اندازه
0.00004 = 4 × 10–5 0.000005 = 5 × 10–6
نماد علمی (scientific notation)
هنگامی که مردم دربارۀ فاصله بین سیاره ها، تعداد دانه های شن، یا مجموع مبلغی که توسط دولت خرج می شود، صحبت می کنند، آنها مجبورند از اعداد خیلی بزرگی استفاده کنند. هنگامی که موضوع بحث به اندازه گیری سلولهای گیاهان یا حیوانات، اندازۀ اتمها، یا سایر چیزهای کوچک اینچنینی، تبدیل شود، مردم از اعداد خیلی کوچک استفاده می کنند. نماد علمی (Scientific notation) یک روش استاندارد برای ثبت کردن این اعداد خیلی کوچک و خیلی بزرگ می باشد، تا آنها در یک خط از یک کتاب جا شوند و همینطور به آسانی با یکدیگر قابل مقایسه باشند. همچنین انجام محاسبات اعداد خیلی بزرگ یا خیلی کوچک، در شکل نماد علمی، بسیار ساده تر می باشد.
یادتان باشد: شکل یک عدد که در نماد علمی نوشته می شود اینطور است:
N × 10aکه در آن، N عددی بین 1 و 10 می باشد (شامل 1 می شود اما مشمول 10 نمی گردد - شما 10 را مورد استفاده قرار نمی دهید، چون دو رقم دارد)، و a یک عدد صحیح (integer) - عددی مثبت یا منفی - می باشد.
شما می توانید اعداد بزرگ و کوچک را در نماد علمی بنویسید، به این شکل که ممیز اعشاری را به نحوی حرکت بدهید که عددی بین 1 تا 10 بسازید، و سپس مشخص سازید، ممیز اعشاری چند خانه حرکت کرده است و عدد 10 را به توانِ تعداد حرکتهای ممیز اعشاری برسانید. اینکه توان 10 مثبت یا منفی باشد، بستگی به این دارد که ممیز اعشاری به سمت راست یا چپ حرکت کرده باشد: حرکت ممیز اعشاری به سمت راست توان را منفی می سازد، حرکت ممیز اعشاری به سمت چپ توان را مثبت می سازد.
برای نوشتن یک عدد در نماد علمی:
-
تعیین کنید ممیز اعشاری در کجای عدد قرار دارد و آن را به سمت چپ یا راست حرکت بدهید تا موقعی که شما دقیقاً یک عدد در سمت چپ ممیز اعشاری داشته باشید.
این کار عددی بین 1 تا 10 را به شما می دهد.
-
تعداد حرکت ممیز اعشاری در خانه ها (ارقام) را نسبت به موقعیت اصلی آن بشمارید.
این قدر مطلق (absolute value) توان شما می باشد.
-
اگر شما ممیز اعشاری اصلی را به سمت چپ حرکت داده باشید، توان شما مثبت می باشد. اگر هم آن را به سمت راست حرکت داده باشید، توان شما منفی می باشد.
-
عدد را در شکل نماد علمی بازنویسی کنید. به این صورت که یک حاصلضرب از عدد بین 1 تا 10 بدست آمده، ضربدر عدد 10 که به توان به دست آمده رسیده است، باشد.
مثال: در اینجا چند عدد را که با نماد علمی نوشته شده اند، می بینید:
-
: یک ممیز اعشاری در انتهای عدد مفروض شده است. ممیز اعشاری را چهار خانه به سمت چپ حرکت بدهید، تا عدد 4.1 را بسازید. توان 10 عدد 4+ می باشد.
-
: ممیز اعشاری 11 خانه به سمت چپ حرکت می کند.
-
: ممیز اعشاری هفت خانه به سمت راست حرکت می کند. این یک عدد خیلی کوچک است و توان آن نیز منفی می باشد.
-
: ممیز اعشاری یک خانه به سمت راست حرکت می کند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: