خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ساده سازی کنید

معادلات خطی (Linear equations) همیشه با شکل زیبای ax + b = c آغاز نمی شوند. گاهی اوقات، به دلیل پیچیدگی کاربرد مربوطه، یک معادله خطی می تواند شامل چندین جمله متغیر و ثابت و تعداد زیادی نمادهای گروه بندی باشد، مانند این معادله:

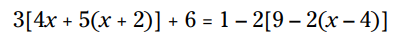
این انواع مختلف نمادهای گروه بندی به منظور ایجاد گروه های تو در تو مورد استفاده قرار می گیرند، و قوانین آنها نیز با توجه به ترتیب انجام عملیات که در فصل 5 بحث شد، روی مسأله شما بکار می روند تا در نهایت متوجه شوید متغیر x چه چیزی را نمایندگی می کند.
هنگامی که عدد یا متغیری داشته باشید که نیاز باشد در هر مقدار داخل یک پرانتز، کروشه، آکولاد، یا ترکیبی از آن نمادهای گروه بندی ضرب گردد، آن عدد یا متغیر را توزیع (distribute) می کنید. توزیع کردن (Distributing) به این معنا می باشد که آن عدد یا متغیر که در کنار نماد گروه بندی قرار دارد در تک تک مقادیر داخل نماد گروه بندی ضرب می گردد. اگر دو یا چند نماد گروه بندی در داخل یکدیگر باشند، آنها تو در تو (nested) می باشند. عبارتهای تو در تو (Nested expressions) با قصد شفافیت و وضوح بیشتر با ترکیبی از نمادهای گروه بندی مختلف همچون پرانتزها، کروشه ها، و آکولادها نوشته می شوند.
در هنگام تو در تو بودن عبارات، قراردادهای زیر مورد استفاده قرار می گیرند:
معادلاتی که شامل نمادهای گروه بندی هستند فرصتهایی را برای گرفتن تصمیمات خردمندانه ارائه می دهند. در برخی موارد شما نیاز دارید که توزیع کنید، از درونی ترین به سمت بیرون، و در مواردی دیگر خردمندانه تر اینست که ابتدا ضرب یا تقسیم کنید. به طور کلی، اگر بیش از دو جمله در کل معادله پیدا کنید، ابتدا توزیع را انجام می دهید.
مثال: این معادله را برای y حل کنید: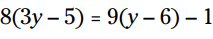
این معادله دارای دو جمله می باشد که شامل نمادهای گروه بندی هستند. ابتدا 8 و 9 را توزیع کنید:
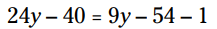
دو جمله ثابت موجود در سمت راست را ترکیب کنید. سپس 9y را از هر دو سمت معادله تفریق کنید:
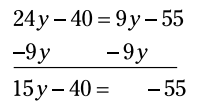
حالا 40 را به هر سمت از معادله بیفزایید. سپس هر سمت را بر 15 تقسیم کنید:
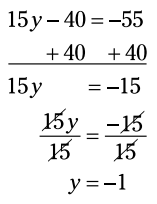
اکنون اجازه بدهید تا راه حل مسأله ای را که در ابتدای این بخش آوردم به شما ارائه بدهم.
مثال: این معادله را برای x حل کنید:
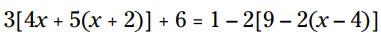
بهترین روش برای نظم بخشیدن به تمامی این عملیات ها اینست که از درون به بیرون ساده سازی را انجام بدهیم. شما پرانتزهای داخل کروشه ها را می بینید. دوجمله ای های داخل پرانتزها دارای ضریب هایی می باشند. من می خواهم با دقت و گام به گام به شما یک برنامه سازمان یافته برای دستیابی به هدف را نشان بدهم.
ابتدا، 5 را روی دوجمله ای داخل پرانتز در سمت چپ معادله توزیع کنید و 2- را بر روی دوجمله ای موجود در پرانتز سمت راست توزیع نمایید:
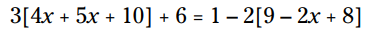
اکنون جملات داخل کروشه ها را ترکیب کنید:
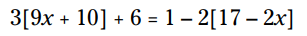
3 را بر روی دو جملۀ موجود در کروشه سمت چپ و 2- را بر روی جملات داخل کروشه در سمت راست معادله، توزیع نمایید:
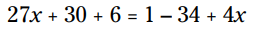
جملات ثابت در هر سمت قابل ترکیب شدن می باشند:
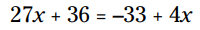
حالا 4x را از هر دو سمت تفریق کنید و 36 را نیز از هر سمت تفریق کنید:
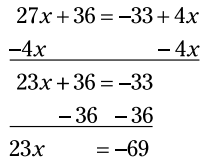
اینک، هر سمت از معادله را بر 23 تقسیم کنید، تا به نتیجه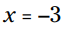 برسید.
برسید.
در این بخش، به شما نشان می دهم کجاها ممکن است ساده تر باشد که به جای اینکه با توزیع آغاز کنید، ابتدا تقسیم بر عددی را انجام بدهید. تنها هشدار من اینست که همیشه هر جمله را بر عدد یکسانی تقسیم (یا ضرب) کنید.
مثال: این معادله را برای z حل کنید: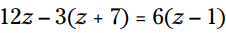
در این معادله، شما سه جمله را می بینید: دو جمله در سمت چپ و یک جمله هم در سمت راست معادله قرار دارد. هر جمله ضریبی دارد که مضربی از 3 می باشد. بنابراین هر جمله را بر 3 تقسیم کنید:
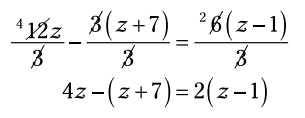
علامت منفی و عدد 2 را توزیع کنید:
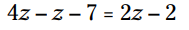
دو جمله متغیر را در سمت چپ ترکیب کنید. سپس 2z را از هر دو سمت تفریق کنید:
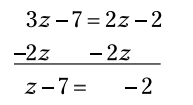
در نهایت، به هر سمت عدد 7 را بیفزایید و خواهید داشت:
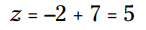
مثال بعدی دو موقعیت متفاوت را با یکدیگر ترکیب کرده است که در واقع یکسان هستند. جملات داخل معادله یا دارای یک ضریب کسری می باشند یا اینکه خودشان در داخل یک کسر هستند. هدف مثال اینست که به شما نشان بدهد هنگامی که هر جمله را ابتدا در عدد یکسانی ضرب می کنید، ترجیح بر اینست که توزیع را در ابتدا انجام بدهید.
مثال: معادله زیر را برای x حل کنید:
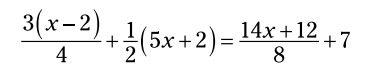
در نگاه اول، این معادله اندکی ناخوشایند به نظر می رسد. اما یک کنش سریع - به این شکل که هر جمله را در 8 ضرب کنیم - از تمامی کسرها مراقبت می کند. شما با یکسری اعداد بزرگ تنها می مانید، اما هنوز هم بهتر از کسرهایی با مخرج غیر مشترک می باشد. من به این دلیل تصمیم گرفتم که آنها را در 8 ضرب کنم چون کوچکترین مخرج مشترک هر جمله (حتی جمله آخر) می باشد. هر کدام از چهار جمله در 8 ضرب می شوند:
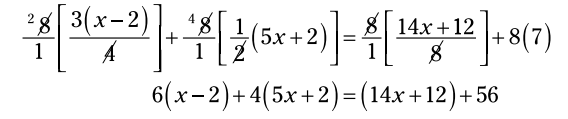
ضرب ها و توزیع را انجام بدهید تا از خطا دور بمانید:
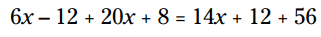
دو جمله متغیر و دو جمله ثابت در سمت چپ می توانند با یکدیگر ترکیب شوند. به همین ترتیب، دو جمله ثابت در سمت راست را با یکدیگر ترکیب کنید:
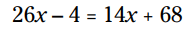
اکنون 14x را از هر سمت تفریق کنید و 4 را به هر سمت بیفزایید:
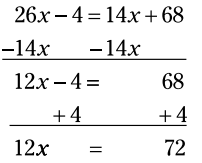
هر سمت معادله را بر 12 تقسیم کنید تا به نتیجه برسید.
برسید.
هنگامی که کسرها را در یک معادله خط می زنید، شما نیاز دارید که تمامی جملات را از ابتدا تا انتها در کوچکترین مخرج مشترک همه کسرها ضرب کنید. در مثال قبلی، کوچکترین مخرج مشترک 8 بود. در معادله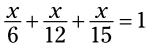 ، کوچکترین مخرج مشترک 60 می باشد.
، کوچکترین مخرج مشترک 60 می باشد.
مخرج مشترک برای کسرهای 6، 12، و 15 برابر با 60 می باشد. چگونه این را بدست آوردم؟ یک روش اینست که حدس بزنیم. روش دیگر اینست که فاکتورگیری اول (prime factorizations) همه اعداد را بنویسیم و آنچه بین همه آنها مشترک می باشد را پیدا کنیم. یک ترفند سریع دیگر اینست که از مراحل زیر استفاده کنیم.

این انواع مختلف نمادهای گروه بندی به منظور ایجاد گروه های تو در تو مورد استفاده قرار می گیرند، و قوانین آنها نیز با توجه به ترتیب انجام عملیات که در فصل 5 بحث شد، روی مسأله شما بکار می روند تا در نهایت متوجه شوید متغیر x چه چیزی را نمایندگی می کند.
عبارت های تو در تو (nested expressions)
هنگامی که عدد یا متغیری داشته باشید که نیاز باشد در هر مقدار داخل یک پرانتز، کروشه، آکولاد، یا ترکیبی از آن نمادهای گروه بندی ضرب گردد، آن عدد یا متغیر را توزیع (distribute) می کنید. توزیع کردن (Distributing) به این معنا می باشد که آن عدد یا متغیر که در کنار نماد گروه بندی قرار دارد در تک تک مقادیر داخل نماد گروه بندی ضرب می گردد. اگر دو یا چند نماد گروه بندی در داخل یکدیگر باشند، آنها تو در تو (nested) می باشند. عبارتهای تو در تو (Nested expressions) با قصد شفافیت و وضوح بیشتر با ترکیبی از نمادهای گروه بندی مختلف همچون پرانتزها، کروشه ها، و آکولادها نوشته می شوند.
در هنگام تو در تو بودن عبارات، قراردادهای زیر مورد استفاده قرار می گیرند:
-
هنگامی که از عبارتهای تو در تو استفاده می کنید، هر نماد گروه بندی باز - همچون پرانتز، کروشه، و آکولاد -
باید یک نماد گروه بندی بسته شدن معادلش
را داشته باشد تا ابتدا و انتهای هر گروه بندی را مشخص نماید.
-
هنگام ساده سازی عبارتهای تو در تو، از درونی ترین گروه آغاز کنید و به ترتیب به سمت بیرونی ترین گروه بندی ادامه بدهید. درونی ترین عبارت آن است که هیچ علامت گروه بندی در داخلش نداشته باشد. آن عبارت را ساده کنید یا با توزیع پرانتزهایش را از بین ببرید. سپس دوباره به سراغ درونی ترین گروه بندی بعدی بروید.
توزیع در ابتدا (Distributing first)
معادلاتی که شامل نمادهای گروه بندی هستند فرصتهایی را برای گرفتن تصمیمات خردمندانه ارائه می دهند. در برخی موارد شما نیاز دارید که توزیع کنید، از درونی ترین به سمت بیرون، و در مواردی دیگر خردمندانه تر اینست که ابتدا ضرب یا تقسیم کنید. به طور کلی، اگر بیش از دو جمله در کل معادله پیدا کنید، ابتدا توزیع را انجام می دهید.
مثال: این معادله را برای y حل کنید:
این معادله دارای دو جمله می باشد که شامل نمادهای گروه بندی هستند. ابتدا 8 و 9 را توزیع کنید:
دو جمله ثابت موجود در سمت راست را ترکیب کنید. سپس 9y را از هر دو سمت معادله تفریق کنید:
حالا 40 را به هر سمت از معادله بیفزایید. سپس هر سمت را بر 15 تقسیم کنید:
اکنون اجازه بدهید تا راه حل مسأله ای را که در ابتدای این بخش آوردم به شما ارائه بدهم.
مثال: این معادله را برای x حل کنید:
بهترین روش برای نظم بخشیدن به تمامی این عملیات ها اینست که از درون به بیرون ساده سازی را انجام بدهیم. شما پرانتزهای داخل کروشه ها را می بینید. دوجمله ای های داخل پرانتزها دارای ضریب هایی می باشند. من می خواهم با دقت و گام به گام به شما یک برنامه سازمان یافته برای دستیابی به هدف را نشان بدهم.
ابتدا، 5 را روی دوجمله ای داخل پرانتز در سمت چپ معادله توزیع کنید و 2- را بر روی دوجمله ای موجود در پرانتز سمت راست توزیع نمایید:
اکنون جملات داخل کروشه ها را ترکیب کنید:
3 را بر روی دو جملۀ موجود در کروشه سمت چپ و 2- را بر روی جملات داخل کروشه در سمت راست معادله، توزیع نمایید:
جملات ثابت در هر سمت قابل ترکیب شدن می باشند:
حالا 4x را از هر دو سمت تفریق کنید و 36 را نیز از هر سمت تفریق کنید:
اینک، هر سمت از معادله را بر 23 تقسیم کنید، تا به نتیجه
ضرب یا تقسیم قبل از توزیع
در این بخش، به شما نشان می دهم کجاها ممکن است ساده تر باشد که به جای اینکه با توزیع آغاز کنید، ابتدا تقسیم بر عددی را انجام بدهید. تنها هشدار من اینست که همیشه هر جمله را بر عدد یکسانی تقسیم (یا ضرب) کنید.
مثال: این معادله را برای z حل کنید:
در این معادله، شما سه جمله را می بینید: دو جمله در سمت چپ و یک جمله هم در سمت راست معادله قرار دارد. هر جمله ضریبی دارد که مضربی از 3 می باشد. بنابراین هر جمله را بر 3 تقسیم کنید:
هشدار: توجه داشته باشید که جمله دوم یک علامت منفی در مقابل دوجمله ای دارد. خیلی مراقب باشید که ردیابی ضریب های منفی را از دست ندهید.
علامت منفی و عدد 2 را توزیع کنید:
دو جمله متغیر را در سمت چپ ترکیب کنید. سپس 2z را از هر دو سمت تفریق کنید:
در نهایت، به هر سمت عدد 7 را بیفزایید و خواهید داشت:
مثال بعدی دو موقعیت متفاوت را با یکدیگر ترکیب کرده است که در واقع یکسان هستند. جملات داخل معادله یا دارای یک ضریب کسری می باشند یا اینکه خودشان در داخل یک کسر هستند. هدف مثال اینست که به شما نشان بدهد هنگامی که هر جمله را ابتدا در عدد یکسانی ضرب می کنید، ترجیح بر اینست که توزیع را در ابتدا انجام بدهید.
مثال: معادله زیر را برای x حل کنید:
در نگاه اول، این معادله اندکی ناخوشایند به نظر می رسد. اما یک کنش سریع - به این شکل که هر جمله را در 8 ضرب کنیم - از تمامی کسرها مراقبت می کند. شما با یکسری اعداد بزرگ تنها می مانید، اما هنوز هم بهتر از کسرهایی با مخرج غیر مشترک می باشد. من به این دلیل تصمیم گرفتم که آنها را در 8 ضرب کنم چون کوچکترین مخرج مشترک هر جمله (حتی جمله آخر) می باشد. هر کدام از چهار جمله در 8 ضرب می شوند:
ضرب ها و توزیع را انجام بدهید تا از خطا دور بمانید:
دو جمله متغیر و دو جمله ثابت در سمت چپ می توانند با یکدیگر ترکیب شوند. به همین ترتیب، دو جمله ثابت در سمت راست را با یکدیگر ترکیب کنید:
اکنون 14x را از هر سمت تفریق کنید و 4 را به هر سمت بیفزایید:
هر سمت معادله را بر 12 تقسیم کنید تا به نتیجه
هنگامی که کسرها را در یک معادله خط می زنید، شما نیاز دارید که تمامی جملات را از ابتدا تا انتها در کوچکترین مخرج مشترک همه کسرها ضرب کنید. در مثال قبلی، کوچکترین مخرج مشترک 8 بود. در معادله
مخرج مشترک برای کسرهای 6، 12، و 15 برابر با 60 می باشد. چگونه این را بدست آوردم؟ یک روش اینست که حدس بزنیم. روش دیگر اینست که فاکتورگیری اول (prime factorizations) همه اعداد را بنویسیم و آنچه بین همه آنها مشترک می باشد را پیدا کنیم. یک ترفند سریع دیگر اینست که از مراحل زیر استفاده کنیم.
-
بزرگترین مخرج را در نظر بگیرید و تمامی مضربهای آن را بررسی کنید تا زمانی که یکی از آنها سایر مخرج ها را به صورت مساوی تقسیم کند.
در مورد این مسأله، 15 بزرگترین مخرج می باشد:
-
: نه 6 و نه 12 هیچکدام 15 را به طور مساوی تقسیم نمی کنند.
-
: تنها 6 عدد 30 را به طور مساوی تقسیم می کند.
-
: نه 6 و نه 12 هیچکدام 15 را به طور مساوی تقسیم نمی کنند.
-
: خودش است!
-
-
هر کسر را در آن مخرج مشترک ضرب کنید:
هنگامی که در این مثال، کسرها را در 60 ضرب کنید، تمامی مخرج ها ناپدید می شوند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: