خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
معادلات درجه دوم (Quadratic Equations)
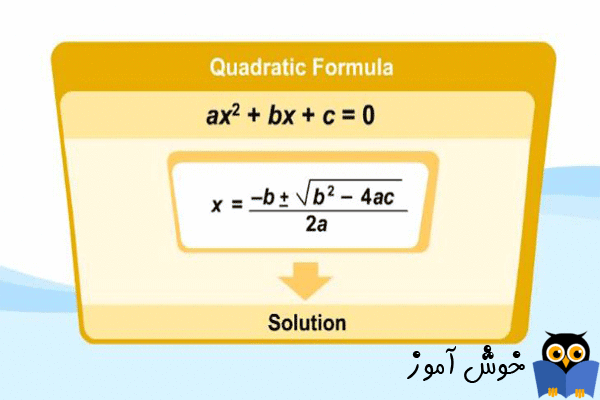
کار کردن با معادلات درجه دوم (Quadratic Equations) به دلیل قابل مدیریت بودنشان لذت بخش می باشد. پیدا کردن یک راه حل یا تصمیم گیری در این باره که آیا راه حلی وجود دارد، نسبتاً آسان می باشد - حداقل در دنیای ریاضی آسان می باشد.

یک معادله درجه دوم، یک عبارت درجه دوم می باشد که یک علامت برابری به آن متصل شده است. مشابه معادلات خطی (linear equations)، روش ها یا فرآیند های خاصی، که جزئیاتشان در این فصل مطرح می شود، برای حل کردن موفقیت آمیز معادلات درجه دوم، بکار گرفته می شوند. رایج ترین تکنیک برای حل کردن این معادلات فاکتورگیری می باشد، همچنین یک قانون سریع و کثیف هم برای یکی از انواع خاص معادلات درجه دوم وجود دارد. با اینحال، من باید به شما این هشدار را بدهم، صرف اینکه شخصی چند عدد و متغیر را به شکل معادله درجه دوم کنار یکدیگر چیده باشد، دلیل نمی شود که الزاماً یک راه حل یا پاسخ برای آن معادله وجود داشته باشد. (در این فصل به شما نشان می دهم که چطور تشخیص بدهید یک معادله درجه دوم پاسخی ندارد.)
معادلات درجه دوم برای جبر و بسیاری از علوم دیگر مهم می باشند. برخی از معادلات درجه دوم می گویند آنچه بالا می رود باید پایین بیاید (یعنی در مورد جاذبه هستند). بقیه معادلات مسیرهایی را که سیاره ها و ستاره ها دنبال می کنند، توصیف می کنند. در کل، معادلات درجه دوم شگفت انگیز هستند و کار کردن با آنها عالی است.
یک معادله درجه دوم (quadratic equation) شامل یک جمله متغیر می باشد که به توان 2 رسیده باشد و هیچ متغیری در آن توان بالاتر از آن ندارد.
یک معادله درجه دوم یک شکل کلی دارد که مشابه این می باشد: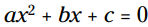 . ثابتهای a، b، و c در معادله اعداد حقیقی هستند، و a نمی تواند برابر با 0 باشد. (اگر a برابر 0 باشد، شما دیگر یک معادله درجه دوم نخواهید داشت.)
. ثابتهای a، b، و c در معادله اعداد حقیقی هستند، و a نمی تواند برابر با 0 باشد. (اگر a برابر 0 باشد، شما دیگر یک معادله درجه دوم نخواهید داشت.)
اگر این معادله برایتان آشنا به نظر می رسد، به این معنا می باشد که شما فصل 9 را خوانده اید، که در مورد فاکتورگیری و کار با عبارتهای درجه دوم (quadratic expressions) می باشد. یادتان باشد: یک عبارت (expression) از یک یا چند جمله تشکیل می شود اما علامت برابری ندارد. اضافه کردن یک علامت برابری کل ماجرا را عوض می کند: اکنون شما یک معادله دارید که چیزی را بیان می کند. اگر پاسخهایی را جایگزین متغیرها کنید، معادله یک بیانیه صحیح را شکل می دهد.
در اینجا چند مثال از معادلات درجه دوم و راه حل آنها را داریم:
یک ویژگی خاص از معادلات درجه دوم اینست که آنها می توانند دو پاسخ کاملاً متفاوت داشته باشند، و اغلب هم همینطور است. همانطورکه در مثالهای قبلی دیدید، سه تا از این معادلات دارای دو پاسخ متفاوت با یکدیگر بودند. آخرین معادله تنها یک پاسخ داشت، اما، از نظر فنی، شما آن پاسخ را دوبار محاسبه می کنید، که به آن ریشۀ مضاعف (double root) می گویند. برخی از معادلات درجه دوم، در صورتی که فقط اعداد حقیقی را در نظر بگیرید، هیچ پاسخی ندارند، اما فعلاً به معادلاتی می چسبیم که پاسخ حقیقی داشته باشند.
من چگونه پاسخ آن مثالها را بدست آوردم؟ من از روشهای حل کردن معادلات درجه دوم استفاده کردم که در این فصل آنها را خواهید یافت. هدف من در این بخش اینست که شما را با این موضوع آشنا سازم که می توانید دو پاسخ کاملاً متفاوت برای یک معادله داشته باشید که هر دو نیز به درستی کار می کنند. با اینحال، اگر نمی توانید در برابر کنجکاویتان مقاومت کنید، می توانید سریعتر از ما در آموزش پیش بروید و به بخشهای مربوطه پرش کنید.
چگونه یک معادله می تواند دو پاسخ داشته باشد؟ در یک برنامه کاربردی یا مسأله داستانی، از کدام پاسخ استفاده می کنید؟ برای مثال، اگر یک مسأله داستانی از شما بپرسد قیمت یک چیز چقدر است، چگونه می توان دو پاسخ صحیح به این پرسش داد؟ خوب، گاهی اوقات برای یک کاربرد دو پاسخ صحیح وجود دارد، اما در واقع یکی از آن پاسخها برای آن وضعیت خاص، معنادار نمی باشد. این پاسخ بی معنا معادله ای را که شما ایجاد کرده اید حل می کند و فقط مانند یک چمدان اضافی همراه شما می آید. هنگامی که با دو پاسخ مواجه می شوید، شما باید تصمیم بگیرید که آیا به پاسخ اضافی توجه کنید یا خیر.
اجازه بدهید دو مثال از مسائلی که از معادلات درجه دوم استفاده می کنند بزنم که به دو پاسخ ختم می شوند. در مثال اول، می توانید ببینید که هر دو پاسخ درست کار می کنند. در مثال دوم، تنها یک پاسخ درست کار می کند.
مثال: یک توپ توسط شخصی که روی یک دیوار با ارتفاع 16 فوت ایستاده است، به هوا پرتاب می شود. ارتفاع توپ (h) به فوت بعد از t ثانیه این معادله درجه دوم را به ما می دهد: . چه زمانی ارتفاع توپ 80 فوت در هوا می باشد؟
. چه زمانی ارتفاع توپ 80 فوت در هوا می باشد؟
در مورد اینکه این معادله را از کجا آورده ام نگران نباشید، این چیزی است که در فیزیک و در بسیاری از کلاسهای ریاضی مورد بحث قرار می گیرد.
من می خواهم بدانم چه زمانی توپ در ارتفاع 80 فوت از سطح زمین قرار می گیرد، بنابراین 80 را در مسأله به جای ارتفاع (h) قرار می دهم:
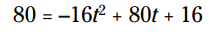
من به صورت اتفاقی می دانم که اگر t برابر با 1 یا 4 باشد، معادله صحیح می باشد. خوب، من واقعاً این پاسخها را به صورت تصادفی نمی دانم و از روشهای موجود در همین فصل برای پیدا کردن پاسخهای معادله درجه دوم استفاده کرده ام. دوباره، من می خواهم به شما نشان بدهم که چگونه ممکن است دو پاسخ کار کنند و هر دو نیز معنا دار باشند.
هنگامیکه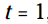 :
:
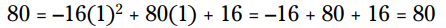
و هنگامیکه :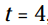
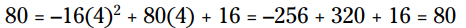
هر دو پاسخ درست کار می کنند! بنابراین این معادله می گوید هنگامی که t برابر با 1 باشد (یعنی بعد از 1 ثانیه) و هنگامی که t برابر با 4 باشد (بعد از 4 ثانیه) ارتفاع توپ 80 فوت در هوا می باشد. در اولین مرتبه (یعنی در ثانیه 1) توپ به سمت بالا می رود و در ارتفاع 80 فوتی قرار دارد، و در مرتبه دوم (یعنی در ثانیه 4) توپ همان ارتفاع را دارد اما به سمت پایین و زمین در حرکت است. اگر شما از ارتفاع 16 فوتی یک توپ را به سمت بالا پرتاپ کنید، سپس توپ می تواند به سمت بالا برود، از سطح ارتفاع 80 فوتی عبور کند، از آن ارتفاع بالاتر نیز برود و سپس در هنگام بازگشت به زمین مجدداً از همان ارتفاع 80 فوتی اما اینبار در جهت رو به پایین عبور نماید.
مسأله بعدی از یک معادله درجه دوم استفاده می کند که دو پاسخ دارد، اما فقط یکی از این پاسخها در مسأله واقعی معنادار می باشد. هر دو پاسخ در معادله به درستی کار می کنند، اما فقط یکی از آنها پاسخ سوال می باشد.
مثال: شما ناظر شرکت Whatchamacallits هستید، و از تابع هزینه زیر برای پیدا کردن مجموع هزینه تولید n واحد از محصول استفاده می کنید: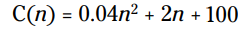 . شما یک سفارش از یک مشتری دریافت می کنید که او می گوید فقط $124 برای کار کردن دارد. آن مشتری چند واحد می تواند خریداری کنید؟
. شما یک سفارش از یک مشتری دریافت می کنید که او می گوید فقط $124 برای کار کردن دارد. آن مشتری چند واحد می تواند خریداری کنید؟
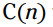 را با 124 جایگزین کنید و معادله به این شکل خواهد شد:
را با 124 جایگزین کنید و معادله به این شکل خواهد شد: 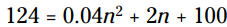 . معادله را برای بدست آوردن n حل کنید، پاسخ های این معادله
. معادله را برای بدست آوردن n حل کنید، پاسخ های این معادله 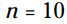 و
و 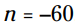 ، هر کدام از این دو پاسخ این معادله را به یک بیانیه صحیح (true statement) تبدیل می کنند:
، هر کدام از این دو پاسخ این معادله را به یک بیانیه صحیح (true statement) تبدیل می کنند: 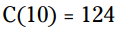 و
و 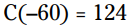 .
.
رسیدن به این دو پاسخ - که یکی از آنها منفی می باشد - در زمانی که از یک معادله برای مدل کردن آنچه که در دنیای واقعی اتفاق می افتد استفاده می کنیم، به وفور پیش می آید. معادله مربوطه معمولاً به صورت عالی با هر دو پاسخ درست کار می کند، اما شما نمی توانید آنرا فراتر از منطق مورد استفاده قرار بدهید.
در این معادله خاص، اینکه از اعداد منفی برای n استفاده کنیم، معنادار نمی باشد، زیرا شما نمی توانید یک تعداد منفی از محصولات را تولید کنید. و در شرایط دیگر همچنین منطقی نیست که از مقادیر بیلیون یا تریلیون برای n استفاده کنیم.
هزینه استفاده از این معادلات زیبا اینست که از آنها باید تحت شرایط منطقی و معقول استفاده کرد.

یک معادله درجه دوم، یک عبارت درجه دوم می باشد که یک علامت برابری به آن متصل شده است. مشابه معادلات خطی (linear equations)، روش ها یا فرآیند های خاصی، که جزئیاتشان در این فصل مطرح می شود، برای حل کردن موفقیت آمیز معادلات درجه دوم، بکار گرفته می شوند. رایج ترین تکنیک برای حل کردن این معادلات فاکتورگیری می باشد، همچنین یک قانون سریع و کثیف هم برای یکی از انواع خاص معادلات درجه دوم وجود دارد. با اینحال، من باید به شما این هشدار را بدهم، صرف اینکه شخصی چند عدد و متغیر را به شکل معادله درجه دوم کنار یکدیگر چیده باشد، دلیل نمی شود که الزاماً یک راه حل یا پاسخ برای آن معادله وجود داشته باشد. (در این فصل به شما نشان می دهم که چطور تشخیص بدهید یک معادله درجه دوم پاسخی ندارد.)
معادلات درجه دوم برای جبر و بسیاری از علوم دیگر مهم می باشند. برخی از معادلات درجه دوم می گویند آنچه بالا می رود باید پایین بیاید (یعنی در مورد جاذبه هستند). بقیه معادلات مسیرهایی را که سیاره ها و ستاره ها دنبال می کنند، توصیف می کنند. در کل، معادلات درجه دوم شگفت انگیز هستند و کار کردن با آنها عالی است.
مربع کردن به سوی درجه دوم
یک معادله درجه دوم (quadratic equation) شامل یک جمله متغیر می باشد که به توان 2 رسیده باشد و هیچ متغیری در آن توان بالاتر از آن ندارد.
یک معادله درجه دوم یک شکل کلی دارد که مشابه این می باشد:
اگر این معادله برایتان آشنا به نظر می رسد، به این معنا می باشد که شما فصل 9 را خوانده اید، که در مورد فاکتورگیری و کار با عبارتهای درجه دوم (quadratic expressions) می باشد. یادتان باشد: یک عبارت (expression) از یک یا چند جمله تشکیل می شود اما علامت برابری ندارد. اضافه کردن یک علامت برابری کل ماجرا را عوض می کند: اکنون شما یک معادله دارید که چیزی را بیان می کند. اگر پاسخهایی را جایگزین متغیرها کنید، معادله یک بیانیه صحیح را شکل می دهد.
در اینجا چند مثال از معادلات درجه دوم و راه حل آنها را داریم:
-
: در این معادله، هیچکدام از ضریبها 0 نمی باشند. دو پاسخ این معادله شامل
و
می باشند.
-
: در این معادله، b برابر با 0 می باشد. پاسخها
و
می باشند.
-
: در این معادله، c برابر با 0 می باشد. پاسخها
و
می باشند.
-
: در این معادله، هم b و هم c برابر با 0 می باشند. این معادله تنها یک پاسخ دارد،
.
یک ویژگی خاص از معادلات درجه دوم اینست که آنها می توانند دو پاسخ کاملاً متفاوت داشته باشند، و اغلب هم همینطور است. همانطورکه در مثالهای قبلی دیدید، سه تا از این معادلات دارای دو پاسخ متفاوت با یکدیگر بودند. آخرین معادله تنها یک پاسخ داشت، اما، از نظر فنی، شما آن پاسخ را دوبار محاسبه می کنید، که به آن ریشۀ مضاعف (double root) می گویند. برخی از معادلات درجه دوم، در صورتی که فقط اعداد حقیقی را در نظر بگیرید، هیچ پاسخی ندارند، اما فعلاً به معادلاتی می چسبیم که پاسخ حقیقی داشته باشند.
من چگونه پاسخ آن مثالها را بدست آوردم؟ من از روشهای حل کردن معادلات درجه دوم استفاده کردم که در این فصل آنها را خواهید یافت. هدف من در این بخش اینست که شما را با این موضوع آشنا سازم که می توانید دو پاسخ کاملاً متفاوت برای یک معادله داشته باشید که هر دو نیز به درستی کار می کنند. با اینحال، اگر نمی توانید در برابر کنجکاویتان مقاومت کنید، می توانید سریعتر از ما در آموزش پیش بروید و به بخشهای مربوطه پرش کنید.
چگونه یک معادله می تواند دو پاسخ داشته باشد؟ در یک برنامه کاربردی یا مسأله داستانی، از کدام پاسخ استفاده می کنید؟ برای مثال، اگر یک مسأله داستانی از شما بپرسد قیمت یک چیز چقدر است، چگونه می توان دو پاسخ صحیح به این پرسش داد؟ خوب، گاهی اوقات برای یک کاربرد دو پاسخ صحیح وجود دارد، اما در واقع یکی از آن پاسخها برای آن وضعیت خاص، معنادار نمی باشد. این پاسخ بی معنا معادله ای را که شما ایجاد کرده اید حل می کند و فقط مانند یک چمدان اضافی همراه شما می آید. هنگامی که با دو پاسخ مواجه می شوید، شما باید تصمیم بگیرید که آیا به پاسخ اضافی توجه کنید یا خیر.
اجازه بدهید دو مثال از مسائلی که از معادلات درجه دوم استفاده می کنند بزنم که به دو پاسخ ختم می شوند. در مثال اول، می توانید ببینید که هر دو پاسخ درست کار می کنند. در مثال دوم، تنها یک پاسخ درست کار می کند.
مثال: یک توپ توسط شخصی که روی یک دیوار با ارتفاع 16 فوت ایستاده است، به هوا پرتاب می شود. ارتفاع توپ (h) به فوت بعد از t ثانیه این معادله درجه دوم را به ما می دهد:
در مورد اینکه این معادله را از کجا آورده ام نگران نباشید، این چیزی است که در فیزیک و در بسیاری از کلاسهای ریاضی مورد بحث قرار می گیرد.
من می خواهم بدانم چه زمانی توپ در ارتفاع 80 فوت از سطح زمین قرار می گیرد، بنابراین 80 را در مسأله به جای ارتفاع (h) قرار می دهم:
من به صورت اتفاقی می دانم که اگر t برابر با 1 یا 4 باشد، معادله صحیح می باشد. خوب، من واقعاً این پاسخها را به صورت تصادفی نمی دانم و از روشهای موجود در همین فصل برای پیدا کردن پاسخهای معادله درجه دوم استفاده کرده ام. دوباره، من می خواهم به شما نشان بدهم که چگونه ممکن است دو پاسخ کار کنند و هر دو نیز معنا دار باشند.
هنگامیکه
و هنگامیکه :
هر دو پاسخ درست کار می کنند! بنابراین این معادله می گوید هنگامی که t برابر با 1 باشد (یعنی بعد از 1 ثانیه) و هنگامی که t برابر با 4 باشد (بعد از 4 ثانیه) ارتفاع توپ 80 فوت در هوا می باشد. در اولین مرتبه (یعنی در ثانیه 1) توپ به سمت بالا می رود و در ارتفاع 80 فوتی قرار دارد، و در مرتبه دوم (یعنی در ثانیه 4) توپ همان ارتفاع را دارد اما به سمت پایین و زمین در حرکت است. اگر شما از ارتفاع 16 فوتی یک توپ را به سمت بالا پرتاپ کنید، سپس توپ می تواند به سمت بالا برود، از سطح ارتفاع 80 فوتی عبور کند، از آن ارتفاع بالاتر نیز برود و سپس در هنگام بازگشت به زمین مجدداً از همان ارتفاع 80 فوتی اما اینبار در جهت رو به پایین عبور نماید.
مسأله بعدی از یک معادله درجه دوم استفاده می کند که دو پاسخ دارد، اما فقط یکی از این پاسخها در مسأله واقعی معنادار می باشد. هر دو پاسخ در معادله به درستی کار می کنند، اما فقط یکی از آنها پاسخ سوال می باشد.
مثال: شما ناظر شرکت Whatchamacallits هستید، و از تابع هزینه زیر برای پیدا کردن مجموع هزینه تولید n واحد از محصول استفاده می کنید:
رسیدن به این دو پاسخ - که یکی از آنها منفی می باشد - در زمانی که از یک معادله برای مدل کردن آنچه که در دنیای واقعی اتفاق می افتد استفاده می کنیم، به وفور پیش می آید. معادله مربوطه معمولاً به صورت عالی با هر دو پاسخ درست کار می کند، اما شما نمی توانید آنرا فراتر از منطق مورد استفاده قرار بدهید.
در این معادله خاص، اینکه از اعداد منفی برای n استفاده کنیم، معنادار نمی باشد، زیرا شما نمی توانید یک تعداد منفی از محصولات را تولید کنید. و در شرایط دیگر همچنین منطقی نیست که از مقادیر بیلیون یا تریلیون برای n استفاده کنیم.
هزینه استفاده از این معادلات زیبا اینست که از آنها باید تحت شرایط منطقی و معقول استفاده کرد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: