خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ریشه گیری در معادلات درجه دوم
شکل کلی معادله درجه دوم (quadratic equation) را در زیر این پاراگراف می بینید. در این شکل هم b و هم c می توانند برابر با 0 باشند. این بخش به شما نشان می دهد اگر b برابر با 0 باشد، حل کردن معادله درجه دوم چقدر زیبا و همینطور چقدر آسان خواهد شد.

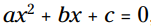
20 مربع کامل (حاصلضرب یک عدد ضربدر خودش) عبارتند از:
اعداد گنگ (irrational number) خاتمه نمی یابند و یا اینکه بعد از ممیز اعشاری دارای الگوی تکرار شونده نمی باشند. برای مثال، ریشه دوم 2 که یک عدد گنگ (اصم) می باشد، برابر با ...1.414213562373 است. یک عدد گنگ هرگز نمی تواند به شکل یک کسر نوشته شود. اعداد گنگ دقیقاً به همان شکلی هستند که نامشان آنها را توصیف می کند: وحشی و غیرقابل پیش بینی. با اینحال، ریشه آنها یک مقدار اعشاری می باشد که می توانید مقدار تقریبی آنها را با ماشین حساب بدست آورید.
اگر نمی توانید برخی از مربع های بزرگتر را شناسایی کنید، نگران نباشید، زیرا آنها به وفور مورد استفاده قرار نخواهند گرفت، و معمولاً به نوعی اشاراتی دریافت می کنید که در هنگام حل مسأله آن عدد یک مربع کامل می باشد. گاهی اوقات این اشارات از یک مسأله داستانی می آید - ممکن است در مورد یک اتاق مربع شکل، یا اضلاع یک مثلث قائم الزاویه صحبت شده باشد. گاهی اوقات اشاره تنها اینست که اگر آن عدد مربع کامل باشد چقدر خوب خواهد بود!
در اینجا یک پیچیدگی ظریف بین مربع ها و ریشه های دوم وجود دارد. معمولاً اگر از شما ریشه دوم 25 را بخواهند، شما در پاسخ خواهید گفت "پنج". خوب، البته صحیح هم هست، اما این فقط ریشه دوم مهمتر می باشد. هنگامی که مشغول حل کردن معادلات درجه دوم هستید، با بیانیه هایی آغاز خواهید کرد که شامل متغیرهایی مربع شده می باشند، بنابراین معمولاً دو پاسخ برای معادله وجود دارد. در مورد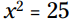 ، این دو پاسخ عبارت از 5+ و 5- می باشند.
، این دو پاسخ عبارت از 5+ و 5- می باشند.
در ادامه قوانین مربوط به برخی از انواع خاص از معادلات درجه دوم را می بینید. در اینجا مراد ما از خاص اینست که b برابر با 0 باشد. این معادلات معمولاً به شکل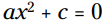 آغاز می شوند، اما c معمولاً منفی می باشد که به شما شکل
آغاز می شوند، اما c معمولاً منفی می باشد که به شما شکل 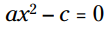 را می دهد و معادله به شکل
را می دهد و معادله به شکل 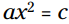 بازنویسی می گردد.
بازنویسی می گردد.
قوانین جبری: اگر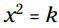 ، سپس
، سپس 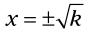 یا اگر
یا اگر 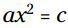 سپس
سپس 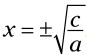 . اگر مربع یک متغیر برابر با عدد k باشد، سپس آن متغیر برابر با ریشه دوم اصلی k یا قرینه آن می باشد.
. اگر مربع یک متغیر برابر با عدد k باشد، سپس آن متغیر برابر با ریشه دوم اصلی k یا قرینه آن می باشد.
مثالهای زیر به شما نشان می دهند چگونه از این قوانین ریشه دوم در معادلات درجه دوم از نوع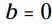 ، استفاده می شود.
، استفاده می شود.
مثال: این معادله را برای x حل کنید: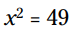
با استفاده از قانون ریشه دوم داریم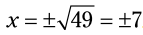 . برای درست آزمایی پاسخها داریم:
. برای درست آزمایی پاسخها داریم: 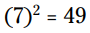 و
و 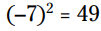 .
.
مثال: این معادله را برای m حل کنید: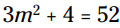
این معادله برای قانون ریشه دوم کاملاً مناسب نمی باشد. به هر دو سمت آن 4- را اضافه می کنیم:
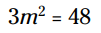
اکنون هر سمت را بر 3 تقسیم می کنیم:
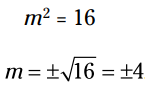
مثال: این معادله را برای p حل کنید: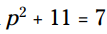
به هر دو سمت معادله 11- را اضافه کنید تا به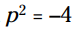 برسید. اوه! چه عددی ضربدر خودش می شود 4-؟ پاسخ اینست : "چنین عددی وجود ندارد!"
برسید. اوه! چه عددی ضربدر خودش می شود 4-؟ پاسخ اینست : "چنین عددی وجود ندارد!"
مثال: این معادله را برای q حل کنید: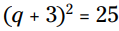
در این مورد، شما با دو پاسخ کاملاً متفاوت روبرو می شوید و نه صرفاً یک عدد و قرینه آن. با استفاده از قانون ریشه دوم (قانون جذر)، داریم:
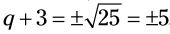
اکنون شما دو معادله خطی (linear equations) متفاوت دارید که باید آنها را حل کنید:

با تفریق 3 از هر دو سمت معادله، دو پاسخ زیر را خواهیم داشت:

این مسأله قطعاً نیاز به درست آزمایی دارد. با جایگزینی 2 در مسأله خواهیم داشت:
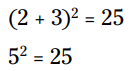
با جایگزینی 8- خواهیم داشت:
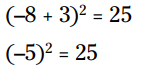
بله، هر دو پاسخ به درستی کار می کنند!

20 مربع کامل (حاصلضرب یک عدد ضربدر خودش) عبارتند از:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400توجه داشته باشید که این اعداد مربع از 1 تا 400 می باشند. در بین این اعداد لیست شده، هیچ مربع کامل دیگری وجود ندارد. یعنی 380 عدد دیگری که بین 1 و 400 وجود دارند مربع کامل (perfect squares) نمی باشند. اعداد مربع کامل همگی دارای ریشه دوم زیبایی می باشند. ریشه دوم (جذر) 121 برابر با 11 می باشد. ریشه دوم 256 برابر با 16 می باشد. آیا این زیبا نیست؟ اما ریشه دوم 200 زیبا نیست. در واقع جذر 200 یک عدد گنگ (irrational number) می باشد.
اعداد گنگ (irrational number) خاتمه نمی یابند و یا اینکه بعد از ممیز اعشاری دارای الگوی تکرار شونده نمی باشند. برای مثال، ریشه دوم 2 که یک عدد گنگ (اصم) می باشد، برابر با ...1.414213562373 است. یک عدد گنگ هرگز نمی تواند به شکل یک کسر نوشته شود. اعداد گنگ دقیقاً به همان شکلی هستند که نامشان آنها را توصیف می کند: وحشی و غیرقابل پیش بینی. با اینحال، ریشه آنها یک مقدار اعشاری می باشد که می توانید مقدار تقریبی آنها را با ماشین حساب بدست آورید.
اگر نمی توانید برخی از مربع های بزرگتر را شناسایی کنید، نگران نباشید، زیرا آنها به وفور مورد استفاده قرار نخواهند گرفت، و معمولاً به نوعی اشاراتی دریافت می کنید که در هنگام حل مسأله آن عدد یک مربع کامل می باشد. گاهی اوقات این اشارات از یک مسأله داستانی می آید - ممکن است در مورد یک اتاق مربع شکل، یا اضلاع یک مثلث قائم الزاویه صحبت شده باشد. گاهی اوقات اشاره تنها اینست که اگر آن عدد مربع کامل باشد چقدر خوب خواهد بود!
در اینجا یک پیچیدگی ظریف بین مربع ها و ریشه های دوم وجود دارد. معمولاً اگر از شما ریشه دوم 25 را بخواهند، شما در پاسخ خواهید گفت "پنج". خوب، البته صحیح هم هست، اما این فقط ریشه دوم مهمتر می باشد. هنگامی که مشغول حل کردن معادلات درجه دوم هستید، با بیانیه هایی آغاز خواهید کرد که شامل متغیرهایی مربع شده می باشند، بنابراین معمولاً دو پاسخ برای معادله وجود دارد. در مورد
نکات فنی: ریشه اصلی یک عدد (principal square root) یک عدد مثبت می باشد، که وقتی در خودش ضرب گردد، عدد اصلی را به شما می دهد. ریشه اصلی عدد 49 برابر با 7 می باشد. هنگامی که برای حل کردن یک معادله ریشه دوم را بدست می آورید، هم ریشه اصلی عدد و هم قرینه آن عدد (همان عدد با علامت منفی) مورد استفاده قرار می گیرند. بنابراین، تحت برخی شرایط، مانند حل کردن معادلات درجه دوم، شما باید آن پاسخ دیگر را نیز در نظر بگیرید.
در ادامه قوانین مربوط به برخی از انواع خاص از معادلات درجه دوم را می بینید. در اینجا مراد ما از خاص اینست که b برابر با 0 باشد. این معادلات معمولاً به شکل
قوانین جبری: اگر
مثالهای زیر به شما نشان می دهند چگونه از این قوانین ریشه دوم در معادلات درجه دوم از نوع
مثال: این معادله را برای x حل کنید:
با استفاده از قانون ریشه دوم داریم
مثال: این معادله را برای m حل کنید:
این معادله برای قانون ریشه دوم کاملاً مناسب نمی باشد. به هر دو سمت آن 4- را اضافه می کنیم:
اکنون هر سمت را بر 3 تقسیم می کنیم:
مثال: این معادله را برای p حل کنید:
به هر دو سمت معادله 11- را اضافه کنید تا به
نکات فنی: ریاضیدانان اعدادی را ایجاد کرده اند که در واقع وجود ندارند بنابراین این مسأله قابل حل می باشد. این اعداد با نام اعداد موهومی (imaginary numbers) شناخته می شوند، اما در این بخش ما با اعداد موهومی سر و کار نخواهیم داشت. بنابراین، اگر به دنبال یک عدد حقیقی (real number) می باشید، این مسأله پاسخی ندارد.
مثال: این معادله را برای q حل کنید:
در این مورد، شما با دو پاسخ کاملاً متفاوت روبرو می شوید و نه صرفاً یک عدد و قرینه آن. با استفاده از قانون ریشه دوم (قانون جذر)، داریم:
اکنون شما دو معادله خطی (linear equations) متفاوت دارید که باید آنها را حل کنید:
با تفریق 3 از هر دو سمت معادله، دو پاسخ زیر را خواهیم داشت:
این مسأله قطعاً نیاز به درست آزمایی دارد. با جایگزینی 2 در مسأله خواهیم داشت:
با جایگزینی 8- خواهیم داشت:
بله، هر دو پاسخ به درستی کار می کنند!
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: