خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
فاکتورگیری از معادلات درجه دوم
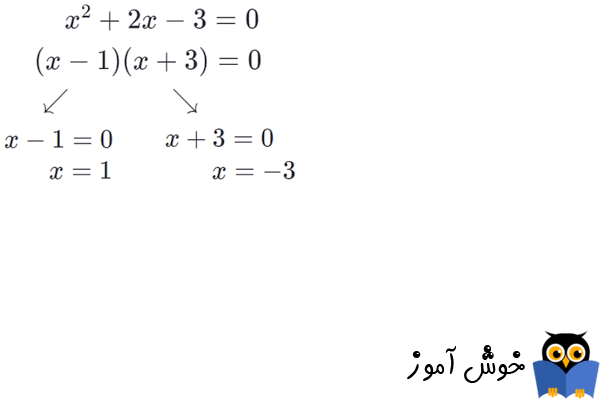
این بخش جایی است که در آن بررسی کردن تمامی روش های فاکتورگیری می تواند واقعاً همراه با موفقیت باشد. (برای جزئیات بیشتر در مورد فاکتورگیری به فصلهای 8، 9، و 10 مراجعه کنید.) در بیشتر معادلات درجه دوم، به جای روش قانون ریشه دوم که در بخش قبل پوشش دادیم، از فاکتورگیری استفاده می شود. قانون ریشه دوم تنها در صورتی استفاده می شود که در معادله درجه دوم  ، مقدار b برابر با 0 باشد. فاکتورگیری زمانی استفاده می شود که c برابر با 0 باشد یا هیچکدام از موارد b و c برابر با 0 نباشند.
، مقدار b برابر با 0 باشد. فاکتورگیری زمانی استفاده می شود که c برابر با 0 باشد یا هیچکدام از موارد b و c برابر با 0 نباشند.

یک ویژگی مهم که همراه با فاکتورگیری برای حل کردن این معادله ها مورد استفاده قرار می گیرد ویژگی ضرب در صفر می باشد. این یک قانون خیلی سر راست می باشد - و حتی معنادار نیز می باشد. از بزرگترین فاکتور مشترک و ویژگی ضرب در صفر برای حل کردن معادلات درجه دوم که در شکل مناسب برای قانون ریشه دوم (square-root rule) نمی باشند، استفاده کنید.
قبل از وارد شدن به مبحث استفاده از فاکتورگیری برای حل کردن معادلات درجه دوم، نیاز دارید که در مورد ویژگی ضرب در صفر بدانید. شما ممکن است بگویید "چه چیزی را باید بدانم؟ صفر در هر عددی ضرب شود هیچ چیزی باقی نمی ماند. صفر همه چیز را محو می کند!" نسبتاً درست است، اما ویژگی خوب دیگر 0 مبنای حل کردن بسیاری از معادلات در جبر می باشد. به خودی خود، 0 هیچ چیزی نیست. آن را به عنوان نتیجه یک مسأله ضرب قرار بدهید، و واقعاً چیزی خواهید داشت: ویژگی ضرب در صفر (multiplication property of zero).
قوانین جبر: ویژگی ضرب در صفر (MPZ: multiplication property of zero) بیان می دارد که اگر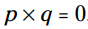 ، سپس یا
، سپس یا 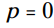 و یا اینکه
و یا اینکه 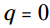 . دست کم یکی از این دو باید برابر با 0 باشند.
. دست کم یکی از این دو باید برابر با 0 باشند.
این موضوع ممکن است بدیهی به نظر برسد، اما در موردش فکر کنید. هیچ عدد دیگری چنین قدرت و تسلطی بر روی سایر اعداد ندارد. اگر شما فرض کنید که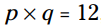 است، نمی توانید چیزی را در مورد p یا q به تنهایی پیش بینی کنید. این متغیرها می توانند هر عددی باشند - مثبت، منفی، کسر، رادیکال، و یا ترکیبی از همه اینها. با این وجود یک حاصلضرب از 0، شما را به یک نتیجه گیری هدایت می کند: یکی از ضریب ها باید برابر با 0 باشد. هیچ راه دیگری برای رسیدن به یک حاصلضرب 0 وجود ندارد. چرا این مسأله باید مهم باشد؟ اجازه بدهید به شما چند معادله و چگونگی کارکرد ویژگی ضرب کردن در صفر را نشان بدهم.
است، نمی توانید چیزی را در مورد p یا q به تنهایی پیش بینی کنید. این متغیرها می توانند هر عددی باشند - مثبت، منفی، کسر، رادیکال، و یا ترکیبی از همه اینها. با این وجود یک حاصلضرب از 0، شما را به یک نتیجه گیری هدایت می کند: یکی از ضریب ها باید برابر با 0 باشد. هیچ راه دیگری برای رسیدن به یک حاصلضرب 0 وجود ندارد. چرا این مسأله باید مهم باشد؟ اجازه بدهید به شما چند معادله و چگونگی کارکرد ویژگی ضرب کردن در صفر را نشان بدهم.
مثال: در این معادله مقدار x را بیابید: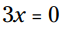
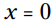 می باشد، زیرا 3 نمی تواند 0 باشد. با استفاده از ویژگی ضرب کردن در صفر، که بیان می کند یکی از فاکتورها باید برابر با 0 باشد، پس مقدار دیگر باید الزاماً 0 باشد تا به حاصلضرب 0 برسیم.
می باشد، زیرا 3 نمی تواند 0 باشد. با استفاده از ویژگی ضرب کردن در صفر، که بیان می کند یکی از فاکتورها باید برابر با 0 باشد، پس مقدار دیگر باید الزاماً 0 باشد تا به حاصلضرب 0 برسیم.
مثال: در معادله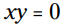 ، مقدار x را بیابید.
، مقدار x را بیابید.
در این معادله شما دو احتمال دارید. اگر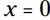 باشد، سپس y می تواند هر عددی، حتی 0 باشد. اگر
باشد، سپس y می تواند هر عددی، حتی 0 باشد. اگر 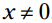 ، در اینصورت بنابر ویژگی ضرب در صفر، y الزاماً باید 0 باشد.
، در اینصورت بنابر ویژگی ضرب در صفر، y الزاماً باید 0 باشد.
مثال: این معادله را برای x حل کنید: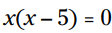
دوباره شما دو احتمال دارید. اگر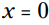 باشد، سپس حاصلضرب
باشد، سپس حاصلضرب 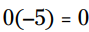 . انتخاب دیگر شما اینست که
. انتخاب دیگر شما اینست که 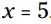 ، که در اینصورت خواهیم داشت
، که در اینصورت خواهیم داشت 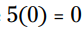 .
.
هنگامی که فقط دو جمله داشته باشید و آن دو جمله دارای فاکتور مشترکی باشند، فاکتورگیری نسبتاً ساده می باشد. این مسأله در مورد معادلات درجه دوم در شکل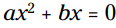 صدق می کند (در این شکل c برابر با 0 می باشد). دو جمله سمت چپ، دست کم دارای فاکتور مشترکی از x می باشند. شما ابتدا بزرگترین فاکتور مشترک (GCF) را پیدا می کند و آن را فاکتور می گیرید، و سپس از ویژگی ضرب در صفر (MPZ) برای حل معادله استفاده می کنید.
صدق می کند (در این شکل c برابر با 0 می باشد). دو جمله سمت چپ، دست کم دارای فاکتور مشترکی از x می باشند. شما ابتدا بزرگترین فاکتور مشترک (GCF) را پیدا می کند و آن را فاکتور می گیرید، و سپس از ویژگی ضرب در صفر (MPZ) برای حل معادله استفاده می کنید.
مثالهای زیر از این واقعیت استفاده می کنند که جمله ثابت برابر با 0 می باشد، و دست کم فاکتور مشترکی از x در هر دو جمله می باشد.
با استفاده از فاکتورگیری این معادله را برای x حل کنید: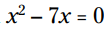
بزرگترین فاکتور مشترک این دوجمله x می باشد، بنابراین سمت چپ معادله را به شکل فاکتورگیری شده می نویسیم:

با استفاده از ویژگی ضرب در صفر (MPZ) که می گوید یا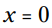 و یا اینکه
و یا اینکه 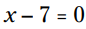 . در اولین حالت x برابر با 0 خواهد بود و در حالت دوم x برابر با 7 خواهد شد.
. در اولین حالت x برابر با 0 خواهد بود و در حالت دوم x برابر با 7 خواهد شد.
مثال: این معادله را برای x حل کنید: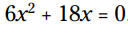
بزرگترین فاکتور مشترک این دو جمله 6x می باشد، بنابراین سمت چپ معادله را به شکل فاکتورگیری شده بنویسید:
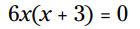
با استفاده از ویژگی ضرب در صفر (MPZ) خواهیم داشت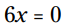 یا
یا 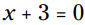 ، که به شما دو پاسخ
، که به شما دو پاسخ 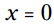 یا
یا 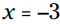 را می دهد.
را می دهد.
از لحاظ فنی، من می توانم سه معادله مختلف برای شکل فاکتورگیری شده بنویسم:
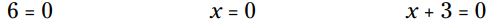
اولین معادله یعنی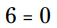 معنایی ندارد - این یک بیانیه غیرممکن می باشد. بنابراین شما یا می توانید برابر قرار دادن ثابت با 0 را نادیده بگیرید یا آن را با متغیر فاکتورگیری شده ترکیب کنید، که هیچ زیانی هم ندارد.
معنایی ندارد - این یک بیانیه غیرممکن می باشد. بنابراین شما یا می توانید برابر قرار دادن ثابت با 0 را نادیده بگیرید یا آن را با متغیر فاکتورگیری شده ترکیب کنید، که هیچ زیانی هم ندارد.
مثال: از آنجا که در بسیاری از معادلات درجه دوم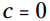 ، سودمند خواهد بود اگر قانون یا فرمولی برای اینکه هر بار پاسخها چه می باشند، داشته باشیم. بنابراین، برای ایجاد یک قانون، در شکل کلی معادله درجه دوم در مواقعی که c برابر با 0 می باشد، معادله را برای x حل کنید:
، سودمند خواهد بود اگر قانون یا فرمولی برای اینکه هر بار پاسخها چه می باشند، داشته باشیم. بنابراین، برای ایجاد یک قانون، در شکل کلی معادله درجه دوم در مواقعی که c برابر با 0 می باشد، معادله را برای x حل کنید: 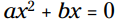
بزرگترین فاکتور مشترک این دو جمله x می باشد، بنابراین معادله را به شکل فاکتورگیری شده بازنویسی می کنیم:
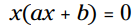
با استفاده از ویژگی ضرب در صفر (MPZ) می توانیم بگوییم که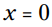 یا
یا  . اولین بخش از این دو پاسخ کاملاً واضح می باشد. این ماجرای
. اولین بخش از این دو پاسخ کاملاً واضح می باشد. این ماجرای 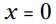 به نظر می رسد هر بار به همین شکل اتفاق می افتد. حل دقیق بخش دوم نیاز به حل کردن یک معادله خطی دارد. b را از هر دو سمت معادله تفریق کنید:
به نظر می رسد هر بار به همین شکل اتفاق می افتد. حل دقیق بخش دوم نیاز به حل کردن یک معادله خطی دارد. b را از هر دو سمت معادله تفریق کنید:
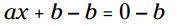
هر دو سمت را بر a تقسیم کنید:
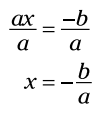
دو پاسخ معادله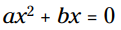 موارد
موارد 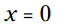 و
و 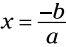 می باشند.
می باشند.
این الگوی قابل شناسایی می تواند به شما کمک کند تا این نوع از معادلات را حل کنید. شما می توانید این را به عنوان یک فرمول و بدون اینکه هر بار نیازی به فاکتور گیری و حل مسأله داشته باشید، مورد استفاده قرار دهید.

یک ویژگی مهم که همراه با فاکتورگیری برای حل کردن این معادله ها مورد استفاده قرار می گیرد ویژگی ضرب در صفر می باشد. این یک قانون خیلی سر راست می باشد - و حتی معنادار نیز می باشد. از بزرگترین فاکتور مشترک و ویژگی ضرب در صفر برای حل کردن معادلات درجه دوم که در شکل مناسب برای قانون ریشه دوم (square-root rule) نمی باشند، استفاده کنید.
ویژگی ضرب در صفر (multiplication property of zero)
قبل از وارد شدن به مبحث استفاده از فاکتورگیری برای حل کردن معادلات درجه دوم، نیاز دارید که در مورد ویژگی ضرب در صفر بدانید. شما ممکن است بگویید "چه چیزی را باید بدانم؟ صفر در هر عددی ضرب شود هیچ چیزی باقی نمی ماند. صفر همه چیز را محو می کند!" نسبتاً درست است، اما ویژگی خوب دیگر 0 مبنای حل کردن بسیاری از معادلات در جبر می باشد. به خودی خود، 0 هیچ چیزی نیست. آن را به عنوان نتیجه یک مسأله ضرب قرار بدهید، و واقعاً چیزی خواهید داشت: ویژگی ضرب در صفر (multiplication property of zero).
قوانین جبر: ویژگی ضرب در صفر (MPZ: multiplication property of zero) بیان می دارد که اگر
این موضوع ممکن است بدیهی به نظر برسد، اما در موردش فکر کنید. هیچ عدد دیگری چنین قدرت و تسلطی بر روی سایر اعداد ندارد. اگر شما فرض کنید که
مثال: در این معادله مقدار x را بیابید:
مثال: در معادله
در این معادله شما دو احتمال دارید. اگر
مثال: این معادله را برای x حل کنید:
دوباره شما دو احتمال دارید. اگر
استفاده از بزرگترین فاکتور مشترک و ویژگی ضرب در صفر برای حل کردن معادلات درجه دوم
هنگامی که فقط دو جمله داشته باشید و آن دو جمله دارای فاکتور مشترکی باشند، فاکتورگیری نسبتاً ساده می باشد. این مسأله در مورد معادلات درجه دوم در شکل
مثالهای زیر از این واقعیت استفاده می کنند که جمله ثابت برابر با 0 می باشد، و دست کم فاکتور مشترکی از x در هر دو جمله می باشد.
با استفاده از فاکتورگیری این معادله را برای x حل کنید:
بزرگترین فاکتور مشترک این دوجمله x می باشد، بنابراین سمت چپ معادله را به شکل فاکتورگیری شده می نویسیم:
با استفاده از ویژگی ضرب در صفر (MPZ) که می گوید یا
مثال: این معادله را برای x حل کنید:
بزرگترین فاکتور مشترک این دو جمله 6x می باشد، بنابراین سمت چپ معادله را به شکل فاکتورگیری شده بنویسید:
با استفاده از ویژگی ضرب در صفر (MPZ) خواهیم داشت
از لحاظ فنی، من می توانم سه معادله مختلف برای شکل فاکتورگیری شده بنویسم:
اولین معادله یعنی
مثال: از آنجا که در بسیاری از معادلات درجه دوم
بزرگترین فاکتور مشترک این دو جمله x می باشد، بنابراین معادله را به شکل فاکتورگیری شده بازنویسی می کنیم:
با استفاده از ویژگی ضرب در صفر (MPZ) می توانیم بگوییم که
هر دو سمت را بر a تقسیم کنید:
دو پاسخ معادله
این الگوی قابل شناسایی می تواند به شما کمک کند تا این نوع از معادلات را حل کنید. شما می توانید این را به عنوان یک فرمول و بدون اینکه هر بار نیازی به فاکتور گیری و حل مسأله داشته باشید، مورد استفاده قرار دهید.
هشدار: فراموش کردن 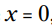 ، که یک نیمه از پاسخ کامل می باشد، اتفاقی است که بطور شگفت انگیزی به وفور پیش می آید. شما متوجه آن x تنهای بیرون پرانتز نمی شوید و فراموش می کنید که آن یکی از دو پاسخ مسأله را به شما می دهد. مراقب باشید.
، که یک نیمه از پاسخ کامل می باشد، اتفاقی است که بطور شگفت انگیزی به وفور پیش می آید. شما متوجه آن x تنهای بیرون پرانتز نمی شوید و فراموش می کنید که آن یکی از دو پاسخ مسأله را به شما می دهد. مراقب باشید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: