خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
کاربرد توابع درجه دوم در زندگی واقعی

توابع درجه دوم (Quadratic functions) مدل های فوق العاده ای برای بسیاری از موقعیتهای زندگی واقعی می باشند. صرفاً بدلیل اینکه مواردی را اسم برده باشیم، شما می توانید آنها را در کاربردهای مالی و کاربردهای فیزیک، ببینید. در این بخش چند نمونه از کاربردهای توابع درجه دوم را برای شما فراهم آورده ایم.

یک شرکت شمع سازی، دریافته است که سودش مبتنی بر تعداد شمعهایی که تولید کرده و به فروش می رساند، می باشد. تابع \(P(x)=-0.05x^2+8x-140\) در این شرکت مورد استفاده قرار می گیرد، در این تابع \(x\) نمایندۀ تعداد شمع ها، و \(P\) مخفف profit (سود) می باشد. شما می توانید از این تابع برای محاسبۀ تعداد شمع هایی که شرکت باید تولید کند تا بالاترین حد ممکن سود را کسب نماید، استفاده کنید.
با قرار دادن \(y=0\) دو طول از مبدأ را بدست می آورید و با فاکتورگیری آن را برای \(x\) حل می کنید:
$$
0=-0.05x^2 + 8x-140 \\[2ex]
0=-0.05(x^2 - 160x+2800) \\[2ex]
0=-0.05(x-20)(x-140) \\[2ex]
x-20=0,x=20 \\[2ex]
x-140=0,x=140
$$
تقاطع \((20,0)\) نشان دهندۀ مکانی است که این تابع (سود) از مقادیر منفی به مقادیر مثبت تغییر می کند. شما به این دلیل این را می دانید که نمودار تابع سود یک سهمی می باشد که رو به سمت پایین باز شده است (زیرا \(a\) منفی است)، بنابراین آغاز و پایان منحنی زیر محور \(X\) نمایان می شود. تقاطع \((140,0)\) جایی را نشان می دهد که سود از مقادیر مثبت به مقادیر منفی تغییر می کند. بنابراین، مقدار بیشینه (maximum value)، یعنی رأس، جایی مابین و بالای دو تقاطع قرار دارد. مختصات \(x\) رأس بین \(20\) و \(140\) قرار دارد. اگر می خواهید این نمودار را دوباره ببینید شکل 3-7 را ببینید.

اکنون از فرمول \(x={-b \over 2a}\) برای یافتن مختصات \(x\) در رأس استفاده کنید، \(x={-8 \over 2(-0.05)}={-8 \over -0.1}=80 \) . عدد \(80\) بین \(20\) و \(140\) قرار دارد. در واقع، در نیمۀ راه بین این دو عدد آرمیده است. حالا می توانید مقدار \(P\) را بیابید (مختصات \(y\) در رأس): \(P(80)=-0.05(80)^2+8(80)-140=-320+640-140=180 \) .
یافته های شما بیان می کنند که اگر این شرکت \(80\) شمع تولید کند و بفروشد، بیشینۀ سود ممکن برابر با \($180\) خواهد بود. این برای \($180\) کار خیلی زیادی به نظر می رسد، اما شاید این شرکت کسب و کار کوچکی را مدیریت می کند. کارهایی از این قبیل به شما نشان می دهند داشتن مدل برای سود، درآمد، و هزینه در کسب و کارها، چقدر حائز اهمیت است، تا شما بتوانید پیش بینی هایتان را داشته باشید و برنامه هایتان را سازماندهی کنید.
یک گروه محلی از جوانان اخیراً با استفاده از "مراسم یک پرتاب کن" پولی را برای خیریه جمع آوری کردند. شرکت کنندگان از حامیان مالی خواستند تا بر اساس یک قول که طی 12 ساعت توپ های بسکتبال را به سبد پرتاب کنند، حمایتشان را انجام بدهند. این یک پروژۀ خیلی موفق بود، هم برای خیریه و هم برای جبر، زیرا شما می توانید تکه های جالبی از اطلاعات را در مورد پرتاب توپ های بسکتبال و تعداد اشتباهاتی که رخ می دهد، بیابید.
شرکت کنندگان طی 12 ساعت توپها را به سبدها پرتاب می کنند، تقریباً \(200\) پرتاب را در هر ساعت امتحان می کنند. معادلۀ درجه دوم \(M(t)={17\over6}t^2 - {77\over3}t+100 \) تعداد پرتابهای اشتباه آنها در هر ساعت را مدل سازی می کند، در این معادله \(t\) زمان در واحد ساعت (که از \(0\) تا \(12\) نامگذاری شده است)، و \(M\) تعداد پرتابهای اشتباه می باشد.
این تابع درجه دوم رو به سمت بالا باز می شود (زیرا \(a\) مثبت می باشد)، بنابراین این تابع دارای یک مقدار کمینه می باشد. شکل 8-7 نمودار این تابع را نشان می دهد.
از روی نمودار، می بینید که مقدار اولیه، یعنی عرض از مبدأ، برابر با \(100\) می باشد. در آغاز، شرکت کنندگان حدود \(100\) پرتاب اشتباه در هر ساعت دارند. خبر خوب اینست که با تمرین بهتر می شوند. \(M(2)=60\) به این معنا می باشد که در ساعت دوم پروژه، شرکت کنندگان فقط \(60\) پرتاب را در هر ساعت از دست می دهند. تعداد اشتباهات پایینتر می رود و سپس دوباره رو به سمت بالا بر می گردد. این را چگونه تفسیر می کنید؟ با وجودیکه شرکت کنندگان با تمرین بهتر و بهتر می شوند، فاکتور خستگی در آنها اثر منفی می گذارد.
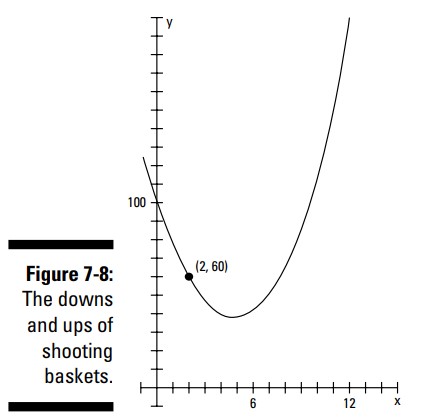
کمترین تعداد اشتباه در چه ساعتی است؟ چه زمانی شرکت کنندگان بهترین پرتاب هایشان را انجام می دهند؟ برای پاسخ دادن به این سوال، رأس سهمی را با استفاده از فرمول مختصات \(x\) بیابید.
$$
\require{cancel}
h={-(-{77\over3}) \over \cancel{2}({17\over \cancel{6}_3})}={77 \over 3} \cdot {3 \over 17}={77\over17}=4{9\over17}
$$
بهترین پرتاب ها در حدود \(4.5\) ساعت بعد از آغاز پروژه اتفاق می افتد. در آن ساعت چند پرتاب اشتباه رخ می دهد؟ عددی که بدست می آورید نشان دهندۀ چیزی است که در کل آن ساعت رخ می دهد ـــ همچنین اندکی غیردقیق می باشد:
$$ M({77\over17})={17\over6}({77\over17})^2-{77\over3}({77\over17})+100 \\[2ex]
={4,271 \over 102} \approx 41.87
$$
این کسر تا دو رقم اعشار گرد شده است. بهترین پرتاب در حدود \(42\) اشتباه در آن ساعت می باشد.
یکی از فعالیتهای محبوب دانش آموزان رشته های مهندسی در فصل بهار در بعضی از دانشگاه ها اینست که بادکنک های پر از آب را از بالای ساختمان مهندسی پرتاب کنند تا به مجسمۀ بنیان گذار دانشگاه، که در فاصلۀ \(25\) فوتی از ساختمان قرار دارد، برخورد کند. پرتاب کننده، بادکنک را به شکل کمان به آسمان می اندازد تا از بالای درختی که در کنار ساختمان قرار دارد، عبور کند. برای اینکه بادکنک به مجسمه برخورد کند، سرعت اولیه و زاویۀ بادکنک باید بدرستی تنظیم گردد. شکل 9-7 یک پرتاب موفق را به شما نشان می دهد.
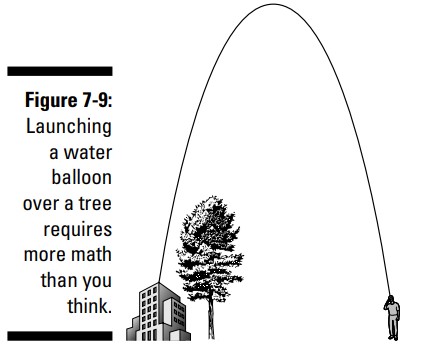
پرتاب امسال موفقیت آمیز بود. دانش آموزان دریافتند که با پرتاب بادکنک های پر از آب با سرعت \(48\) فوت بر ثانیه در یک زاویۀ دقیق، می توانند مجسمه را هدف قرار دهند. این معادله ای است که آنها برای نمایش دادن مسیر بادکنک ها تدبیر کرده اند: \(H(t)=-2t^2+48t+60 \) . \(t\) نشان دهندۀ تعداد ثانیه ها، و \(H\) ارتفاع بادکنک در واحد فوت می باشد. از روی این تابع درجه دوم می توانید به سوالات زیر پاسخ دهید:

فروش شمع ها
یک شرکت شمع سازی، دریافته است که سودش مبتنی بر تعداد شمعهایی که تولید کرده و به فروش می رساند، می باشد. تابع \(P(x)=-0.05x^2+8x-140\) در این شرکت مورد استفاده قرار می گیرد، در این تابع \(x\) نمایندۀ تعداد شمع ها، و \(P\) مخفف profit (سود) می باشد. شما می توانید از این تابع برای محاسبۀ تعداد شمع هایی که شرکت باید تولید کند تا بالاترین حد ممکن سود را کسب نماید، استفاده کنید.
با قرار دادن \(y=0\) دو طول از مبدأ را بدست می آورید و با فاکتورگیری آن را برای \(x\) حل می کنید:
$$
0=-0.05x^2 + 8x-140 \\[2ex]
0=-0.05(x^2 - 160x+2800) \\[2ex]
0=-0.05(x-20)(x-140) \\[2ex]
x-20=0,x=20 \\[2ex]
x-140=0,x=140
$$
تقاطع \((20,0)\) نشان دهندۀ مکانی است که این تابع (سود) از مقادیر منفی به مقادیر مثبت تغییر می کند. شما به این دلیل این را می دانید که نمودار تابع سود یک سهمی می باشد که رو به سمت پایین باز شده است (زیرا \(a\) منفی است)، بنابراین آغاز و پایان منحنی زیر محور \(X\) نمایان می شود. تقاطع \((140,0)\) جایی را نشان می دهد که سود از مقادیر مثبت به مقادیر منفی تغییر می کند. بنابراین، مقدار بیشینه (maximum value)، یعنی رأس، جایی مابین و بالای دو تقاطع قرار دارد. مختصات \(x\) رأس بین \(20\) و \(140\) قرار دارد. اگر می خواهید این نمودار را دوباره ببینید شکل 3-7 را ببینید.

اکنون از فرمول \(x={-b \over 2a}\) برای یافتن مختصات \(x\) در رأس استفاده کنید، \(x={-8 \over 2(-0.05)}={-8 \over -0.1}=80 \) . عدد \(80\) بین \(20\) و \(140\) قرار دارد. در واقع، در نیمۀ راه بین این دو عدد آرمیده است. حالا می توانید مقدار \(P\) را بیابید (مختصات \(y\) در رأس): \(P(80)=-0.05(80)^2+8(80)-140=-320+640-140=180 \) .
یافته های شما بیان می کنند که اگر این شرکت \(80\) شمع تولید کند و بفروشد، بیشینۀ سود ممکن برابر با \($180\) خواهد بود. این برای \($180\) کار خیلی زیادی به نظر می رسد، اما شاید این شرکت کسب و کار کوچکی را مدیریت می کند. کارهایی از این قبیل به شما نشان می دهند داشتن مدل برای سود، درآمد، و هزینه در کسب و کارها، چقدر حائز اهمیت است، تا شما بتوانید پیش بینی هایتان را داشته باشید و برنامه هایتان را سازماندهی کنید.
پرتاب کردن توپ بسکتبال
یک گروه محلی از جوانان اخیراً با استفاده از "مراسم یک پرتاب کن" پولی را برای خیریه جمع آوری کردند. شرکت کنندگان از حامیان مالی خواستند تا بر اساس یک قول که طی 12 ساعت توپ های بسکتبال را به سبد پرتاب کنند، حمایتشان را انجام بدهند. این یک پروژۀ خیلی موفق بود، هم برای خیریه و هم برای جبر، زیرا شما می توانید تکه های جالبی از اطلاعات را در مورد پرتاب توپ های بسکتبال و تعداد اشتباهاتی که رخ می دهد، بیابید.
شرکت کنندگان طی 12 ساعت توپها را به سبدها پرتاب می کنند، تقریباً \(200\) پرتاب را در هر ساعت امتحان می کنند. معادلۀ درجه دوم \(M(t)={17\over6}t^2 - {77\over3}t+100 \) تعداد پرتابهای اشتباه آنها در هر ساعت را مدل سازی می کند، در این معادله \(t\) زمان در واحد ساعت (که از \(0\) تا \(12\) نامگذاری شده است)، و \(M\) تعداد پرتابهای اشتباه می باشد.
این تابع درجه دوم رو به سمت بالا باز می شود (زیرا \(a\) مثبت می باشد)، بنابراین این تابع دارای یک مقدار کمینه می باشد. شکل 8-7 نمودار این تابع را نشان می دهد.
از روی نمودار، می بینید که مقدار اولیه، یعنی عرض از مبدأ، برابر با \(100\) می باشد. در آغاز، شرکت کنندگان حدود \(100\) پرتاب اشتباه در هر ساعت دارند. خبر خوب اینست که با تمرین بهتر می شوند. \(M(2)=60\) به این معنا می باشد که در ساعت دوم پروژه، شرکت کنندگان فقط \(60\) پرتاب را در هر ساعت از دست می دهند. تعداد اشتباهات پایینتر می رود و سپس دوباره رو به سمت بالا بر می گردد. این را چگونه تفسیر می کنید؟ با وجودیکه شرکت کنندگان با تمرین بهتر و بهتر می شوند، فاکتور خستگی در آنها اثر منفی می گذارد.

کمترین تعداد اشتباه در چه ساعتی است؟ چه زمانی شرکت کنندگان بهترین پرتاب هایشان را انجام می دهند؟ برای پاسخ دادن به این سوال، رأس سهمی را با استفاده از فرمول مختصات \(x\) بیابید.
$$
\require{cancel}
h={-(-{77\over3}) \over \cancel{2}({17\over \cancel{6}_3})}={77 \over 3} \cdot {3 \over 17}={77\over17}=4{9\over17}
$$
بهترین پرتاب ها در حدود \(4.5\) ساعت بعد از آغاز پروژه اتفاق می افتد. در آن ساعت چند پرتاب اشتباه رخ می دهد؟ عددی که بدست می آورید نشان دهندۀ چیزی است که در کل آن ساعت رخ می دهد ـــ همچنین اندکی غیردقیق می باشد:
$$ M({77\over17})={17\over6}({77\over17})^2-{77\over3}({77\over17})+100 \\[2ex]
={4,271 \over 102} \approx 41.87
$$
این کسر تا دو رقم اعشار گرد شده است. بهترین پرتاب در حدود \(42\) اشتباه در آن ساعت می باشد.
پرتاب یک بادکنک پر از آب
یکی از فعالیتهای محبوب دانش آموزان رشته های مهندسی در فصل بهار در بعضی از دانشگاه ها اینست که بادکنک های پر از آب را از بالای ساختمان مهندسی پرتاب کنند تا به مجسمۀ بنیان گذار دانشگاه، که در فاصلۀ \(25\) فوتی از ساختمان قرار دارد، برخورد کند. پرتاب کننده، بادکنک را به شکل کمان به آسمان می اندازد تا از بالای درختی که در کنار ساختمان قرار دارد، عبور کند. برای اینکه بادکنک به مجسمه برخورد کند، سرعت اولیه و زاویۀ بادکنک باید بدرستی تنظیم گردد. شکل 9-7 یک پرتاب موفق را به شما نشان می دهد.

پرتاب امسال موفقیت آمیز بود. دانش آموزان دریافتند که با پرتاب بادکنک های پر از آب با سرعت \(48\) فوت بر ثانیه در یک زاویۀ دقیق، می توانند مجسمه را هدف قرار دهند. این معادله ای است که آنها برای نمایش دادن مسیر بادکنک ها تدبیر کرده اند: \(H(t)=-2t^2+48t+60 \) . \(t\) نشان دهندۀ تعداد ثانیه ها، و \(H\) ارتفاع بادکنک در واحد فوت می باشد. از روی این تابع درجه دوم می توانید به سوالات زیر پاسخ دهید:
-
ارتفاع ساختمان چقدر است؟
حل کردن سوال اول احتمالاً برای شما آسان است. پرتاب در زمان \(t=0\)، یعنی مقدار اولیۀ تابع، رخ می دهد. وقتیکه \(t=0\) ، سپس \(H(0)=-2(0)^2+48(0)+60=0+0+60=60 \) . ارتفاع ساختمان \(60\) فوت می باشد.
-
بادکنک چقدر ارتفاع می گیرد؟
پاسخ سوال دوم را با پیدا کردن رأس سهمی می دهید: \(t={-48 \over 2(-2)}={-48 \over -4}=12\) . این به شما \(t\) را می دهد، یعنی تعداد ثانیه هایی که طول می کشد تا بادکنک به بالاترین ارتفاعش برسد ـــ \(12\) ثانیه بعد از پرتاب بادکنک به نقطۀ اوجش می رسد. پاسخ را در معادله جایگذاری کنید تا ارتفاع را بدست آورید: \(H(12)=-2(12)^2+48(12)+60=-288+576+60=348\) . بادکنک تا \(348\) فوت اوج می گیرد.
-
اگر ارتفاع مجسمه \(10\) فوت باشد، چند ثانیه بعد از پرتاب طول می کشد تا بادکنک به مجسمه برسد؟
برای حل کردن سومین پرسش، از این واقعیت که مجسمه \(10\) فوت ارتفاع دارد، استفاده کنید. شما می خواهید بدانید چه زمانی \(H=10\) می شود. \(H\) را در معادله با \(10\) جایگزین کنید و آن را با فاکتورگیری برای بدست آوردن \(t\) حل کنید:
$$
10=-2t^2+48t+60 \\[2ex]
0=-2t^2+48t+50 \\[2ex]
=-2(t^2-24t-25) \\[2ex]
=-2(t-25)(t+1) \\[2ex]
t-25=0,t=25 \\[2ex]
t+1=0,t=-1
$$
طبق معادله، \(t\) می تواند \(25\) یا \(-1\) باشد. در اینجا \(-1\) واقعاً هیچ معنایی ندارد، زیرا شما نمی توانید در زمان رو به عقب برگردید. با این حال، \(25\) ثانیه، به شما می گوید چقدر طول می کشد تا بادکنک به مجسمه برسد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: