خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تقسیم ترکیبی (synthetic division)

از تقسیم ترکیبی (synthetic division) برای تست لیست ریشه های ممکن برای یک چندجمله ای که با استفاده از قضیۀ ریشۀ گویا به آنها رسیده اید، استفاده می کنید. در آموزش های پیشین همین فصل به طور مفصل در مورد قضیۀ ریشۀ گویا (Rational Root Theorem) صحبت کردیم. تقسیم ترکیبی روشی برای تقسیم یک چندجمله ای بر روی یک دوجمله ای، تنها با استفاده از ضریب جملات می باشد. این روش سریع، شسته و رفته، و بسیار دقیق می باشد ـــ معمولاً حتی خیلی دقیقتر از تقسیم های طولانی ـــ و از بیشتر اطلاعاتی که در بخشهای قبلی این فصل مطرح کردیم، استفاده می کند، تمامی این آموزشها را کنار هم بگذارید تا به دنبال ریشه ها/صفرها/تقاطع ها در چندجمله ایها بگردید.

بسته به منظوری که تقسیم ترکیبی را برای آن انجام می دهید، شما می توانید نتایجتان را به سه روش مختلف تفسیر کنید. من هر کدام از این روشها را در بخشهای بعدی تشریح خواهم کرد.
هنگامیکه می خواهید از تقسیم ترکیبی برای سنجش ریشه ها در یک چندجمله ای استفاده کنید، آخرین عدد در ردیف پایینی از تقسیم ترکیبی مسألۀ شما، نتایج را به شما می گوید. اگر آن عدد صفر باشد، تقسیم شما باقیمانده ای ندارد، و عدد مربوطه یک ریشه می باشد. این واقعیت که باقیمانده ای وجود ندارد، به این معنا می باشد که دوجمله ای نمایش داده شده، چند جمله ای را به طور مساوی بخش می کند. آن عدد یک ریشه است زیرا دوجمله ای مربوطه یک فاکتور می باشد.
به عنوان مثال، چندجمله ایِ \( y = x^5 + 5x^4 – 2x^3 – 28x^2 – 8x + 32 \) وقتیکه \(y=0\) باشد، دارای صفرها (یا ریشه ها) می باشد. شما از روی توان \(5\) که بر روی اولین \(x\) قرار دارد، می توانید بگویید که تا پنج ریشه حقیقی ممکن است بیابید. با استفاده از قانون علامتهای دکارت، می توانید دو یا صفر ریشۀ حقیقی مثبت بیابید (زیرا شامل دو تغییر علامت می باشد). با جایگزین کردن \(-x\) به جای \(x\) ، چندجمله ای به شکل زیر در می آید: \( y = –x^5 + 5x^4 + 2x^3 – 28x^2 + 8x + 32 \) . دوباره، با استفاده از قانون علامتهای دکارت، می توانید سه یا یک ریشۀ حقیقی منفی بیابید. (شمارش تعداد ریشه های مثبت و منفی، در هنگام حدس زدن اینکه ریشه ها ممکن است چه باشند، به شما کمک می کند.)
اکنون، با استفاده از قضیۀ ریشۀ گویا، لیست ریشه های گویای بالقوۀ شما عبارت از \(\pm1,\pm2,\pm4,\pm8,\pm16,\pm32\) می باشند. شما یکی از اینها را انتخاب می کنید و تقسیم ترکیبی را بکار می گیرید.
این را به ذهنتان بسپارید که در این مورد اعداد کوچکتر بهترند، فرآیندی که در ادامه آمده است نشان می دهد که حدس \(x=1\) یک ریشه می باشد.
مراحل انجام تقسیم ترکیبی بر روی یک چندجمله ای برای یافتن ریشه های آن به شرح زیر می باشد:
آخرین ورودی در پایین یک صفر می باشد، بنابراین می دانید که \(1\) ، یک ریشه می باشد. اکنون، می توانید یک تقسیم ترکیبی اصلاح شده را برای سنجش ریشه بعدی مورد استفاده قرار دهید؛ شما صرفاً اعداد ابتدا تا انتهای ردیف پایین را به جز صفر وارد شده در سمت راست آن، مورد استفاده قرار می دهید. (این مقادیر در واقع ضریب هایی از خارج قسمت می باشند.)
اگر حدس بعدی شما اینست که ببینید آیا \(x=-1\) یک ریشه می باشد، تقسیم ترکیبی اصلاح شده به شکل زیر ظاهر خواهد شد:
$$
\begin{array}{c|rrrrr}
{\color{red}{-1}} & 1 & 6 & 4 & -24 & -32 \\[3ex]
& \downarrow & -1 & -5 & 1 & 23 \\ \hline
& 1 & 5 & -1 & -23 & {\color{blue}{-9}}
\end{array}
$$
آخرین ورودی در ردیف پایین صفر نمی باشد، بنابراین \(-1\) یک ریشه نیست.
یک حدس زنندۀ خوب در میان شما تصمیم می گیرد تا مقادیر \(x=2\) ، \(x=-4\) ، \(x=-2\) ، و دوباره مقدار \(x=-2\) (برای مرتبه دوم) تست کند. این مقادیر، سایر ریشه ها را نشان می دهند، و تقسیم ترکیبی برای تمامی این حدس ها شبیه موارد زیر می باشد:
ابتدا \(x=2\) را تست کنید،
$$
\begin{array}{c|rrrrr}
{\color{red}{2}} & 1 & 6 & 4 & -24 & -32 \\[3ex]
& \downarrow & 2 & 16 & 40 & 32 \\ \hline
& 1 & 8 & 20 & 16 & {\color{blue}{0}}
\end{array}
$$
آخرین عدد در ردیف پایینی برابر با \(0\) می باشد. این باقیماندۀ تقسیم است. حالا صرفاً به تمامی اعداد قبل از \(0\) بنگرید؛ آنها ضریبهای جدیدی هستند که باید تقسیم کنید. توجه کنید که حالا آخرین ضریب برابر با \(16\) می باشد، بنابراین می توانید لیست ریشه های ممکنتان را اصلاح کنید تا فقط فاکتورهایی از \(16\) باشند. حالا، بر \(-4\) تقسیم می کنیم:
$$
\begin{array}{c|rrrr}
{\color{red}{-4}} & 1 & 8 & 20 & 16 \\[3ex]
& \downarrow & -4 & -16 & -16 \\ \hline
& 1 & 4 & 4 & {\color{blue}{0}}
\end{array}
$$
در تقسیم بعدی، فقط فاکتورهایی از \(4\) را لحاظ می کنید:
این مرتبه، بر \(-2\) تقسیم کنید،
$$
\begin{array}{c|rrr}
{\color{red}{-2}} & 1 & 4 & 4 \\[3ex]
& \downarrow & -2 & -4 \\ \hline
& 1 & 2 & {\color{blue}{0}}
\end{array}
$$
آخرین عدد در ردیف پایینی برابر با \(0\) می باشد، بنابراین \(-2\) یک ریشه است. تقسیم را تکرار کنید، و درخواهید یافت که \(-2\) یک ریشۀ مضاعف (double root) می باشد:
$$
\begin{array}{c|rr}
{\color{red}{-2}} & 1 & 2 \\[3ex]
& \downarrow & -2 \\ \hline
& 1 & {\color{blue}{0}}
\end{array}
$$
هنگامی که عدد \(1\) را در ردیف آخر قبل از صفر می بینید، کار شما خاتمه یافته است.
اکنون تمامی اعدادی را که به صورت برابر تقسیم شده اند جمع آوری می کنید ـــ ریشه های معادله ـــ و از آنها برای نوشتن پاسخ معادله که برابر با صفر قرار داده شده است یا برای نوشتن شکل فاکتورگیری شدۀ چندجمله ای یا برای ترسیم نمودار این اعداد به عنوان طول از مبدأ استفاده می کنید.
پیدا کردن ریشه های یک چندجمله ای تنها بهانه ای که شما برای استفاده از تقسیم ترکیبی دارید، نمی باشد. شما همچنین می توانید از تقسیم ترکیبی به عنوان جایگزینی برای فرآیند طولانی و زمان بر تقسیم یک چندجمله ای بر یک دو جمله ای، استفاده کنید. تقسیم هایی شبیه این در مسأله های حسابان (calculus) ـــ در مواقعی که می خواهید عبارتها را ساده تر کنید ـــ به وفور یافت می شوند.
چندجمله ای می تواند در هر درجه ای باشد؛ دوجمله ای باید در شکل \(x+c\) یا \(x-c\) باشد، و ضریب \(x\) یک می باشد. این ممکن است نسبتاً محدود کننده به نظر آید، اما در همین دسته بندی شما می توانید تعداد بسیار زیادی از تقسیم های طولانی را بگنجانید، بنابراین داشتن یک روش سریع و کارآمد برای انجام این مسأله های تقسیم پایه ای، بسیار سودمند خواهد بود.
برای استفاده از تقسیم ترکیبی جهت تقسیم کردن یک چندجمله ای بر روی یک دوجمله ای، ابتدا چندجمله ای را در ترتیب نزولی توانهایش می نویسید، فقدان توان را با صفر نشان بدهید. عددی را که در ابتدا قرار می دهید معکوس عدد موجود در دوجمله ای می باشد. بنابراین، اگر چندجمله ایِ \(2x^5+3x^4-8x^2-5x+2\) را بر روی دوجمله ای \(x+2\) تقسیم می کنید، مشابه چیزی که در زیر نشان داده شده است، عدد \(-2\) را در تقسیم ترکیبی استفاده نمایید:
$$
\begin{array}{c|rrrrrr}
{\color{red}{-2}} & 2 & 3 & 0 & -8 & -5 & 2 \\[3ex]
& \downarrow & -4 & 2 & -4 & 24 & -38 \\ \hline
& 2 & -1 & 2 & -12 & 19 & {\color{blue}{-36}}
\end{array}
$$
همانطور که می بینید، آخرین ورودی در ردیف پایین صفر نمی باشد. اگر به دنبال ریشه های یک معادلۀ چندجمله ای می باشید، این واقعیت به شما می گوید که \(-2\) یک ریشه نمی باشد. در این مورد، از آنجا که شما مشغول کار بر روی یک کاربرد تقسیم طولانی می باشید (هدف شما از این تقسیم ساده سازی عبارتی می باشد)، \(-4\) باقیماندۀ تقسیم می باشد ـــ به عبارت دیگر، این تقسیم مساوی از آب در نیامده است.
شما پاسخ (خارج قسمت) این مسألۀ تقسیم را از روی ضریبهای ردیف پایین در تقسیم ترکیبی، بدست می آورید. شما با توانی که یک واحد از توان چندجمله ای اصلی کوچکتر باشد، آغاز می کنید، و از تمامی ضریبها استفاده می کنید، و در ضریبهای متوالی بعدی، هر بار یک واحد توان را کاهش می دهید. آخرین ضریب، باقیماندۀ تقسیم می باشد، که آن را بر روی مقسوم علیه (divisor) می نویسید.
در اینجا مسألۀ تقسیم و پاسخ آن را می بینید. مسأله تقسیم اصلی ابتدا نوشته شده است. بعد از مسأله، شما ضریبهای حاصل از تقسیم ترکیبی را که در مقابل متغیرهایشان نوشته شده اند، می بینید ـــ با یک واحد کمتر از درجۀ مسأله اصلی آغاز شده اند. باقیمانده یعنی \(-36\) به صورت کسری بر روی مقسوم علیه، یعنی \(x+2\)، نوشته شده است.
$$ (2x^5+3x^4-8x^2-5x+2) \div (x+2) = 2x^4-x^3+2x^2-12x+19-{36 \over x+2} $$
در دو بخش قبلی، از تقسیم ترکیبی برای تست کردن ریشه های یک معادلۀ چندجمله ای و سپس برای انجام یک تقسیم طولانی استفاده کردید. شما از فرآیند تقسیم ترکیبی یکسانی استفاده کردید، اما نتایج را به طور متفاوتی تفسیر کرده و مورد استفاده قرار دادید. در عین حال، در این بخش، کاربرد دیگری از تقسیم ترکیبی، شامل قضیۀ باقیمانده را ارائه می کنم. هنگامی که بدنبال ریشه ها یا پاسخ های یک معادلۀ چندجمله ای می گردید، همواره تمایل دارید که باقیماندۀ تقسیم ترکیبی برابر با صفر باشد. در این بخش، درخواهید یافت چگونه از آن باقیمانده های مزاحم که صفر نمی باشند، استفاده کنید.
برای مثال، در مسألۀ تقسیم بخش قبل، \( (2x^5 + 3x^4 –8x^2 – 5x + 2) \div (x + 2) \) باقیمانده \(-36\) شد. بنابراین، بنابر قضیۀ باقیمانده، برای این تابع خواهیم داشت:
$$ f (x) =2x^5 + 3x^4 – 8x^2 – 5x + 2, f(–2) = –36 $$
قضیۀ باقیمانده در مسأله های یافتن ریشه بسیار سودمند واقع می شوند، زیرا درخواهید یافت که انجام تقسیم ترکیبی بسیار ساده تر می باشد، به جای اینکه به طور تکراری ضرب و جمع کنید، اعداد را در متغیرها جایگذاری می کنید، اعداد را به توانهای بالا می رسانید، آنها را در ضریبهایشان تقسیم می کنید، و سپس جملات را با یکدیگر ترکیب می کنید.
برای مثال، استفاده از قضیۀ باقیمانده برای یافتن \(f(3)\) وقتیکه
\( f(x) = x^8 – 3x^7 + 2x^5 – 14x^3 + x^2 – 15x + 11 \) ، در این مورد شما می توانید تقسیم ترکیبی را بر روی \(3\) و با استفاده از ضریبها به شکل زیر انجام بدهید:
$$
\begin{array}{c|rrrrrrrrr}
{\color{red}{3}} & 1 & -3 & 0 & 2 & 0 & -14 & 1 & -15 & 11 \\[3ex]
& \downarrow & 3 & 0 & 0 & 6 & 18 & 12 & 39 & 72 \\ \hline
& 1 & 0 & 0 & 2 & 6 & 4 & 13 & 24 & {\color{blue}{83}}
\end{array}
$$
باقیماندۀ این تقسیم بر \(x-3\) برابر با \(83\) می باشد، با استفاده از قضیۀ باقیمانده داریم، \(f(3)=83\) . این فرآیند را با فرآیند جایگزینی \(3\) در تابع مقایسه کنید:
$$ f(3) = (3)^8 – 3(3)^7 + 2(3)^5 – 14(3)^3 + (3)^2 – 15(3) + 11 $$
این اعداد واقعاً بزرگ می گردند. برای مثال، \(3^7=6,561\) . هنگامی که از تقسیم ترکیبی و قضیۀ باقیمانده استفاده می کنید، اعداد بیشتر قابل مدیریت می باشند.

بسته به منظوری که تقسیم ترکیبی را برای آن انجام می دهید، شما می توانید نتایجتان را به سه روش مختلف تفسیر کنید. من هر کدام از این روشها را در بخشهای بعدی تشریح خواهم کرد.
استفاده از تقسیم ترکیبی برای سنجش ریشه ها
هنگامیکه می خواهید از تقسیم ترکیبی برای سنجش ریشه ها در یک چندجمله ای استفاده کنید، آخرین عدد در ردیف پایینی از تقسیم ترکیبی مسألۀ شما، نتایج را به شما می گوید. اگر آن عدد صفر باشد، تقسیم شما باقیمانده ای ندارد، و عدد مربوطه یک ریشه می باشد. این واقعیت که باقیمانده ای وجود ندارد، به این معنا می باشد که دوجمله ای نمایش داده شده، چند جمله ای را به طور مساوی بخش می کند. آن عدد یک ریشه است زیرا دوجمله ای مربوطه یک فاکتور می باشد.
به عنوان مثال، چندجمله ایِ \( y = x^5 + 5x^4 – 2x^3 – 28x^2 – 8x + 32 \) وقتیکه \(y=0\) باشد، دارای صفرها (یا ریشه ها) می باشد. شما از روی توان \(5\) که بر روی اولین \(x\) قرار دارد، می توانید بگویید که تا پنج ریشه حقیقی ممکن است بیابید. با استفاده از قانون علامتهای دکارت، می توانید دو یا صفر ریشۀ حقیقی مثبت بیابید (زیرا شامل دو تغییر علامت می باشد). با جایگزین کردن \(-x\) به جای \(x\) ، چندجمله ای به شکل زیر در می آید: \( y = –x^5 + 5x^4 + 2x^3 – 28x^2 + 8x + 32 \) . دوباره، با استفاده از قانون علامتهای دکارت، می توانید سه یا یک ریشۀ حقیقی منفی بیابید. (شمارش تعداد ریشه های مثبت و منفی، در هنگام حدس زدن اینکه ریشه ها ممکن است چه باشند، به شما کمک می کند.)
اکنون، با استفاده از قضیۀ ریشۀ گویا، لیست ریشه های گویای بالقوۀ شما عبارت از \(\pm1,\pm2,\pm4,\pm8,\pm16,\pm32\) می باشند. شما یکی از اینها را انتخاب می کنید و تقسیم ترکیبی را بکار می گیرید.
نکته: به طور کلی در هنگام استفاده از تقسیم ترکیبی، شما باید ابتدا با اعداد کوچکتر آغاز کنید، بنابراین \(1\) ، \(-1\) ، \(2\) ، \(-2\) ، و به همین ترتیب را مورد استفاده قرار دهید.
این را به ذهنتان بسپارید که در این مورد اعداد کوچکتر بهترند، فرآیندی که در ادامه آمده است نشان می دهد که حدس \(x=1\) یک ریشه می باشد.
مراحل انجام تقسیم ترکیبی بر روی یک چندجمله ای برای یافتن ریشه های آن به شرح زیر می باشد:
-
چندجمله ای را به ترتیب نزولی توانهایش بنویسید. هر توانی را که وجود نداشته باشد با صفر جایگزین کنید تا ضریبش را نشان دهید.
در این مورد، با خوش شانسی مواجه شدید. چندجمله ای در ترتیب صحیحش می باشد:
$$ y = x^5 + 5x^4 – 2x^3 – 28x^2 – 8x + 32 $$
-
ضریب ها را همراه با صفرها، در یک ردیف بنویسید.
$$
\begin{array}{c c c c c c}
& 1 & 5 & -2 & -28 & -8 & 32
\end{array}
$$
-
عددی را که می خواهید بر روی آن تقسیم کنید در جلوی ردیف ضرایب، قرار بدهید، و آن را با یک نیم جعبه جدا کنید.
در این مورد، حدس مربوطه \(x=1\) می باشد.
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\
\end{array}
$$
-
یک خط افقی زیر ردیف ضریب ها بکشید، فضایی را برای اعداد زیر ضرایب خالی بگذارید.
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\[3ex]
\\ \hline
\end{array}
$$
-
اولین ضریب را مستقیماً زیر خط بیاورید.
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\[3ex]
& \downarrow \\ \hline
& 1
\end{array}
$$
-
عددی را که پایین آورده اید بر عددی که تقسیم را بر آن انجام می دهید، ضرب کنید. حاصلضرب بدست آمده را زیر ضریب دوم بنویسید.
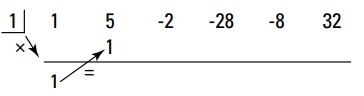
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\[3ex]
& \downarrow & 1 \\ \hline
& 1
\end{array}
$$
-
این حاصلضرب و ضریب دوم را با هم جمع بزنید و نتیجه را زیر خط بنویسید.
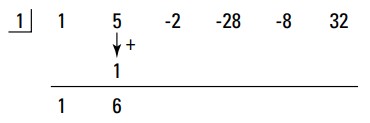
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\[3ex]
& \downarrow & 1 \\ \hline
& 1 & 6
\end{array}
$$
-
فرآیند ضرب/جمع را که در مرحله 6 و 7 مشاهده کردید با بقیه ضرایب نیز تکرار کنید.
$$
\begin{array}{c|rrrrrr}
{\color{red}{1}} & 1 & 5 & -2 & -28 & -8 & 32 \\[3ex]
& \downarrow & 1 & 6 & 4 & -24 & -32 \\ \hline
& 1 & 6 & 4 & -24 & -32 & {\color{blue}0}
\end{array}
$$
آخرین ورودی در پایین یک صفر می باشد، بنابراین می دانید که \(1\) ، یک ریشه می باشد. اکنون، می توانید یک تقسیم ترکیبی اصلاح شده را برای سنجش ریشه بعدی مورد استفاده قرار دهید؛ شما صرفاً اعداد ابتدا تا انتهای ردیف پایین را به جز صفر وارد شده در سمت راست آن، مورد استفاده قرار می دهید. (این مقادیر در واقع ضریب هایی از خارج قسمت می باشند.)
اگر حدس بعدی شما اینست که ببینید آیا \(x=-1\) یک ریشه می باشد، تقسیم ترکیبی اصلاح شده به شکل زیر ظاهر خواهد شد:
$$
\begin{array}{c|rrrrr}
{\color{red}{-1}} & 1 & 6 & 4 & -24 & -32 \\[3ex]
& \downarrow & -1 & -5 & 1 & 23 \\ \hline
& 1 & 5 & -1 & -23 & {\color{blue}{-9}}
\end{array}
$$
آخرین ورودی در ردیف پایین صفر نمی باشد، بنابراین \(-1\) یک ریشه نیست.
یک حدس زنندۀ خوب در میان شما تصمیم می گیرد تا مقادیر \(x=2\) ، \(x=-4\) ، \(x=-2\) ، و دوباره مقدار \(x=-2\) (برای مرتبه دوم) تست کند. این مقادیر، سایر ریشه ها را نشان می دهند، و تقسیم ترکیبی برای تمامی این حدس ها شبیه موارد زیر می باشد:
ابتدا \(x=2\) را تست کنید،
$$
\begin{array}{c|rrrrr}
{\color{red}{2}} & 1 & 6 & 4 & -24 & -32 \\[3ex]
& \downarrow & 2 & 16 & 40 & 32 \\ \hline
& 1 & 8 & 20 & 16 & {\color{blue}{0}}
\end{array}
$$
آخرین عدد در ردیف پایینی برابر با \(0\) می باشد. این باقیماندۀ تقسیم است. حالا صرفاً به تمامی اعداد قبل از \(0\) بنگرید؛ آنها ضریبهای جدیدی هستند که باید تقسیم کنید. توجه کنید که حالا آخرین ضریب برابر با \(16\) می باشد، بنابراین می توانید لیست ریشه های ممکنتان را اصلاح کنید تا فقط فاکتورهایی از \(16\) باشند. حالا، بر \(-4\) تقسیم می کنیم:
$$
\begin{array}{c|rrrr}
{\color{red}{-4}} & 1 & 8 & 20 & 16 \\[3ex]
& \downarrow & -4 & -16 & -16 \\ \hline
& 1 & 4 & 4 & {\color{blue}{0}}
\end{array}
$$
در تقسیم بعدی، فقط فاکتورهایی از \(4\) را لحاظ می کنید:
این مرتبه، بر \(-2\) تقسیم کنید،
$$
\begin{array}{c|rrr}
{\color{red}{-2}} & 1 & 4 & 4 \\[3ex]
& \downarrow & -2 & -4 \\ \hline
& 1 & 2 & {\color{blue}{0}}
\end{array}
$$
آخرین عدد در ردیف پایینی برابر با \(0\) می باشد، بنابراین \(-2\) یک ریشه است. تقسیم را تکرار کنید، و درخواهید یافت که \(-2\) یک ریشۀ مضاعف (double root) می باشد:
$$
\begin{array}{c|rr}
{\color{red}{-2}} & 1 & 2 \\[3ex]
& \downarrow & -2 \\ \hline
& 1 & {\color{blue}{0}}
\end{array}
$$
هنگامی که عدد \(1\) را در ردیف آخر قبل از صفر می بینید، کار شما خاتمه یافته است.
اکنون تمامی اعدادی را که به صورت برابر تقسیم شده اند جمع آوری می کنید ـــ ریشه های معادله ـــ و از آنها برای نوشتن پاسخ معادله که برابر با صفر قرار داده شده است یا برای نوشتن شکل فاکتورگیری شدۀ چندجمله ای یا برای ترسیم نمودار این اعداد به عنوان طول از مبدأ استفاده می کنید.
تقسیم بر یک دوجمله ای به شیوۀ ترکیبی
پیدا کردن ریشه های یک چندجمله ای تنها بهانه ای که شما برای استفاده از تقسیم ترکیبی دارید، نمی باشد. شما همچنین می توانید از تقسیم ترکیبی به عنوان جایگزینی برای فرآیند طولانی و زمان بر تقسیم یک چندجمله ای بر یک دو جمله ای، استفاده کنید. تقسیم هایی شبیه این در مسأله های حسابان (calculus) ـــ در مواقعی که می خواهید عبارتها را ساده تر کنید ـــ به وفور یافت می شوند.
چندجمله ای می تواند در هر درجه ای باشد؛ دوجمله ای باید در شکل \(x+c\) یا \(x-c\) باشد، و ضریب \(x\) یک می باشد. این ممکن است نسبتاً محدود کننده به نظر آید، اما در همین دسته بندی شما می توانید تعداد بسیار زیادی از تقسیم های طولانی را بگنجانید، بنابراین داشتن یک روش سریع و کارآمد برای انجام این مسأله های تقسیم پایه ای، بسیار سودمند خواهد بود.
برای استفاده از تقسیم ترکیبی جهت تقسیم کردن یک چندجمله ای بر روی یک دوجمله ای، ابتدا چندجمله ای را در ترتیب نزولی توانهایش می نویسید، فقدان توان را با صفر نشان بدهید. عددی را که در ابتدا قرار می دهید معکوس عدد موجود در دوجمله ای می باشد. بنابراین، اگر چندجمله ایِ \(2x^5+3x^4-8x^2-5x+2\) را بر روی دوجمله ای \(x+2\) تقسیم می کنید، مشابه چیزی که در زیر نشان داده شده است، عدد \(-2\) را در تقسیم ترکیبی استفاده نمایید:
$$
\begin{array}{c|rrrrrr}
{\color{red}{-2}} & 2 & 3 & 0 & -8 & -5 & 2 \\[3ex]
& \downarrow & -4 & 2 & -4 & 24 & -38 \\ \hline
& 2 & -1 & 2 & -12 & 19 & {\color{blue}{-36}}
\end{array}
$$
همانطور که می بینید، آخرین ورودی در ردیف پایین صفر نمی باشد. اگر به دنبال ریشه های یک معادلۀ چندجمله ای می باشید، این واقعیت به شما می گوید که \(-2\) یک ریشه نمی باشد. در این مورد، از آنجا که شما مشغول کار بر روی یک کاربرد تقسیم طولانی می باشید (هدف شما از این تقسیم ساده سازی عبارتی می باشد)، \(-4\) باقیماندۀ تقسیم می باشد ـــ به عبارت دیگر، این تقسیم مساوی از آب در نیامده است.
شما پاسخ (خارج قسمت) این مسألۀ تقسیم را از روی ضریبهای ردیف پایین در تقسیم ترکیبی، بدست می آورید. شما با توانی که یک واحد از توان چندجمله ای اصلی کوچکتر باشد، آغاز می کنید، و از تمامی ضریبها استفاده می کنید، و در ضریبهای متوالی بعدی، هر بار یک واحد توان را کاهش می دهید. آخرین ضریب، باقیماندۀ تقسیم می باشد، که آن را بر روی مقسوم علیه (divisor) می نویسید.
در اینجا مسألۀ تقسیم و پاسخ آن را می بینید. مسأله تقسیم اصلی ابتدا نوشته شده است. بعد از مسأله، شما ضریبهای حاصل از تقسیم ترکیبی را که در مقابل متغیرهایشان نوشته شده اند، می بینید ـــ با یک واحد کمتر از درجۀ مسأله اصلی آغاز شده اند. باقیمانده یعنی \(-36\) به صورت کسری بر روی مقسوم علیه، یعنی \(x+2\)، نوشته شده است.
$$ (2x^5+3x^4-8x^2-5x+2) \div (x+2) = 2x^4-x^3+2x^2-12x+19-{36 \over x+2} $$
قضیۀ باقیمانده (Remainder Theorem)
در دو بخش قبلی، از تقسیم ترکیبی برای تست کردن ریشه های یک معادلۀ چندجمله ای و سپس برای انجام یک تقسیم طولانی استفاده کردید. شما از فرآیند تقسیم ترکیبی یکسانی استفاده کردید، اما نتایج را به طور متفاوتی تفسیر کرده و مورد استفاده قرار دادید. در عین حال، در این بخش، کاربرد دیگری از تقسیم ترکیبی، شامل قضیۀ باقیمانده را ارائه می کنم. هنگامی که بدنبال ریشه ها یا پاسخ های یک معادلۀ چندجمله ای می گردید، همواره تمایل دارید که باقیماندۀ تقسیم ترکیبی برابر با صفر باشد. در این بخش، درخواهید یافت چگونه از آن باقیمانده های مزاحم که صفر نمی باشند، استفاده کنید.
قوانین جبر: قضیۀ باقیمانده: هنگامی که چندجمله ایِ
\( f(x)=a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1x^1 + a_0 \)
بر روی دوجمله ایِ \(x-c\) تقسیم گردد، باقیماندۀ این تقسیم برابر با \(f(c)\) می باشد.
\( f(x)=a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1x^1 + a_0 \)
بر روی دوجمله ایِ \(x-c\) تقسیم گردد، باقیماندۀ این تقسیم برابر با \(f(c)\) می باشد.
برای مثال، در مسألۀ تقسیم بخش قبل، \( (2x^5 + 3x^4 –8x^2 – 5x + 2) \div (x + 2) \) باقیمانده \(-36\) شد. بنابراین، بنابر قضیۀ باقیمانده، برای این تابع خواهیم داشت:
$$ f (x) =2x^5 + 3x^4 – 8x^2 – 5x + 2, f(–2) = –36 $$
قضیۀ باقیمانده در مسأله های یافتن ریشه بسیار سودمند واقع می شوند، زیرا درخواهید یافت که انجام تقسیم ترکیبی بسیار ساده تر می باشد، به جای اینکه به طور تکراری ضرب و جمع کنید، اعداد را در متغیرها جایگذاری می کنید، اعداد را به توانهای بالا می رسانید، آنها را در ضریبهایشان تقسیم می کنید، و سپس جملات را با یکدیگر ترکیب می کنید.
برای مثال، استفاده از قضیۀ باقیمانده برای یافتن \(f(3)\) وقتیکه
\( f(x) = x^8 – 3x^7 + 2x^5 – 14x^3 + x^2 – 15x + 11 \) ، در این مورد شما می توانید تقسیم ترکیبی را بر روی \(3\) و با استفاده از ضریبها به شکل زیر انجام بدهید:
$$
\begin{array}{c|rrrrrrrrr}
{\color{red}{3}} & 1 & -3 & 0 & 2 & 0 & -14 & 1 & -15 & 11 \\[3ex]
& \downarrow & 3 & 0 & 0 & 6 & 18 & 12 & 39 & 72 \\ \hline
& 1 & 0 & 0 & 2 & 6 & 4 & 13 & 24 & {\color{blue}{83}}
\end{array}
$$
باقیماندۀ این تقسیم بر \(x-3\) برابر با \(83\) می باشد، با استفاده از قضیۀ باقیمانده داریم، \(f(3)=83\) . این فرآیند را با فرآیند جایگزینی \(3\) در تابع مقایسه کنید:
$$ f(3) = (3)^8 – 3(3)^7 + 2(3)^5 – 14(3)^3 + (3)^2 – 15(3) + 11 $$
این اعداد واقعاً بزرگ می گردند. برای مثال، \(3^7=6,561\) . هنگامی که از تقسیم ترکیبی و قضیۀ باقیمانده استفاده می کنید، اعداد بیشتر قابل مدیریت می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: