خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
یافتن معکوس ماتریس ها

معکوس ماتریس ها مشابه معکوس اعداد عمل می کنند. قرینۀ (additive inverse) یک عدد که به آن عضو معکوس در جمع نیز گفته می شود، چیزی است که به آن عدد می افزایید تا حاصلجمع آن صفر گردد. به عنوان مثال، قرینۀ عدد \(2\) برابر با \(-2\) می باشد، و قرینۀ عدد \(-3.14159\) برابر با \(3.14159\) می باشد. به اندازۀ کافی ساده می باشد.

همچنین در جبر چیزی با نام وارون ضربی (multiplicative inverse) ـــ به آن معکوس ضربی نیز گفته می شود ـــ وجود دارد. وارون ضربی به شما عدد یک را می دهد. به عنوان مثال، وارون ضربیِ عدد \(2\) برابر با \({1\over2}\) می باشد.
جمع کردن یا ضرب کردن در معکوس ها همواره به شما عضو خنثی (identity element) را نتیجه می دهد. قبل از آنکه بتوانید معکوس ماتریس ها را پیدا کنید، نیاز دارید تا همانی ها (identities) را درک کنید، بنابراین جزئیات مربوط به همانی ها را در اینجا پوشش داده ام.
شما می توانید عدد صفر را با عنوان عضو خنثی در جمع برچسب گذاری کنید، زیرا افزودن صفر به یک عدد، به آن عدد امکان می دهد تا هویت (identity) خودش را حفظ کند. عضو خنثی در جمع، برای ماتریس ها برابر با ماتریس صفر (zero matrix) می باشد. هنگامی که یک ماتریس صفر را به هر ماتریس دیگری با ابعاد برابر، اضافه می کنید، ماتریس اصلی تغییری نمی کند.
تمامی ماتریس ها دارای قرینه می باشند ـــ فرقی نمی کند ابعاد آن ماتریس چه باشد. در مورد وارون ضربیِ ماتریس ها قضیه اینطور نیست. برخی از ماتریس ها دارای وارون ضربی می باشند و برخی دیگر خیر. در ادامه در این رابطه بیشتر خواهید دانست.
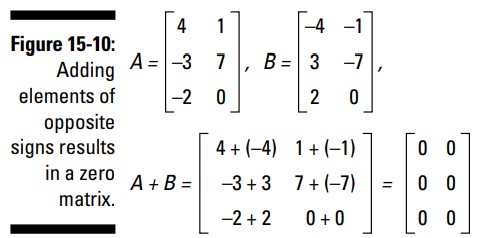
شما می توانید عدد یک را به عنوان عضو خنثی ضربی (multiplicative identity) برچسب گذاری کنید، زیرا ضرب کردن یک عدد در یک، مقدار آن را تغییر نمی دهد ـــ هویتش را حفظ می کند.

شبیه همانی ضربی در یک ماتریس، وارون ضربی یک ماتریس به اندازۀ آن انطباق پذیر نیست. هنگامی که دو ماتریس را در یکدیگر ضرب می کنید، ضرب و جمع های فراوانی را صورت می دهید، و تغییرات زیادی را در ابعاد مشاهده خواهید کرد. به این دلیل، ماتریس ها و معکوس های ضربی آنها، همواره ماتریس های مربعی می باشند؛ ماتریس های غیرمربعی دارای وارون ضربی نمی باشند.
در شکل 12-15 ، من ماتریس \(B\) و وارون آن \(B^{-1}\) را در یکدیگر ضرب نموده ام، سپس با تغییر دادن ترتیب آنها دوباره ضرب را تکرار کرده ام؛ نتیجۀ این فرآیند در هر دو بار برابر با ماتریس همانی شده است.
همۀ ماتریس های مربعی دارای معکوس نمی باشند. اما در مورد آنهایی که دارای معکوس ضربی هستند، شما روشی برای یافتن معکوس ضربی آن ماتریس ها دارید. شما همیشه قبل از شروع کار نمی دانید که آیا ماتریس مربوطه دارای معکوس هست یا نه، اما همچنانکه وارد فرآیند می شوید موضوع برای شما آشکار می گردد. اولین فرآیند یا الگوریتم (algorithm) ـــ الگوریتم یک فرآیند یا روال می باشد که نتیجه ای را تولید می کند ـــ که شما می توانید از آن برای ماتریس هایی در هر اندازه استفاده کنید، در ادامه آمده است. همچنین در مورد ماتریس های \(2 \times 2\) یک روش خاص وجود دارد که در ادامه به آن هم خواهیم پرداخت.
برای حل کردن جهت یافتن معکوس یک ماتریس، این مراحل را دنبال کنید:
به عنوان مثال، فرض کنید می خواهید ماتریس \(M\) را که در ادامه نشان داده شده است، برای یافتن معکوس آن حل کنید. ابتدا یک ماتریس همانی با ابعاد \(3 \times 3\) در سمت راست درایه های ماتریس \(M\) ایجاد می کنید. هدف اینست که درایه های موجود در سمت چپ را با عملیات های سطری به یک ماتریس همانی تبدیل کنید.
$$
M=
\begin{bmatrix}
1&2&4\\
-3&-5&-6\\
2&-3&-36\\
\end{bmatrix}
$$
$$
\begin{bmatrix}
1&2&4&1&0&0\\
-3&-5&-6&0&1&0\\
2&-3&-36&0&0&1\\
\end{bmatrix}
$$
این ماتریس همانی دارای مجموعه ای از یک ها به صورت مورب می باشد، که صفرها در پایین و بالای آنها قرار گرفته اند. اولین چیز برای ایجاد ماتریس همانی مد نظرتان اینست که در زیر عدد یک موجود در بالا و سمت چپ ماتریس، صفرهایی را بدست آورید. در اینجا عملیات سطری مورد نیاز برای رسیدن به این هدف را می بینید:
در ادامه نتیجۀ این عملیات های سطری را می بینید. نمادهای موجود بر روی فلش ها که بین دو ماتریس قرار دارند، عملیات های سطری را برای شما توصیف می کنند.
$$
\begin{bmatrix}
1&2&4&1&0&0\\
-3&-5&-6&0&1&0\\
2&-3&-36&0&0&1\\
\end{bmatrix}
\underset{\overset{(-2)R_1+R_3=R_3}{\longrightarrow}}{\overset{(3)R_1+R_2=R_2}{\longrightarrow}}
\begin{bmatrix}
1&2&4&1&0&0\\
0&1&6&3&1&0\\
0&-7&-44&-2&0&1\\
\end{bmatrix}
$$
حالا، در بالا و پایین این \(1\) نیاز به صفرهایی دارید، بنابراین این مراحل را دنبال می کنید:
$$
\begin{bmatrix}
1&2&4&1&0&0\\
0&1&6&3&1&0\\
0&-7&-44&-2&0&1\\
\end{bmatrix}
\underset{\overset{(7)R_2+R_3=R_3}{\longrightarrow}}{\overset{(-2)R_2+R_1=R_1}{\longrightarrow}}
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&-2&19&7&1\\
\end{bmatrix}
$$
اکنون نیاز دارید تا درایۀ موجود در سطر سوم و ستون سوم از ماتریس را به \(1\) تبدیل کنید، بنابراین سطر مربوطه را در \(-0.5\) ضرب می کنید؛ این ضرب برابر با تقسیم کردن سطر مربوطه بر \(-2\) می باشد.
$$
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&-2&19&7&1\\
\end{bmatrix}
\overset{(-0.5)R_3=R_3}{\longrightarrow}
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
شما یک مجموعه عملیات سطری دیگر نیاز دارید تا صفرهای موجود در بالای آخرین \(1\) از مجموعه یک های مورب را بدست آورید:
اکنون یک ماتریس \(3 \times 3\) همانی در سمت چپ و یک ماتریس \(3 \times 3\) در سمت راست دارید . درایه های موجود در ماتریس سمت راست، ماتریس معکوس یعنی ماتریس \(M^{-1}\) را شکل می دهند. حاصلضرب ماتریس \(M\) و معکوس آن یعنی \(M^{-1}\) ، ماتریس همانی می شوند. در ادامه دو مرحلۀ آخر و پاسخ نهایی نشان داده شده اند.
$$
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
\underset{\overset{(-6)R_3+R_2=R_2}{\longrightarrow}}{\overset{(8)R_3+R_1=R_1}{\longrightarrow}}
\begin{bmatrix}
1&0&0&-81&-30&-4\\
0&1&0&60&22&3\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
$$
M^{-1}=
\begin{bmatrix}
-81&-30&-4\\
60&22&3\\
-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
تصویر زیر درست آزمایی پاسخ بدست آمده را نشان می دهد ـــ نشان می دهد که \(M \cdot M^{-1}\) برابر با ماتریس همانی می باشد:
$$
M \cdot M^{-1}=
\begin{bmatrix}
1&2&4\\
-3&-5&-6\\
2&-3&-36\\
\end{bmatrix}
\cdot
\begin{bmatrix}
-81&-30&-4\\
60&22&3\\
-9.5&-3.5&-0.5\\
\end{bmatrix}
=
\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&1\\
\end{bmatrix}
$$
شما برای یافتن معکوس ماتریس های \(2\times2\) قانون خاصی را در اختیار دارید. برای پیاده سازی قانون یافتن معکوس ماتریس \(2\times2\) ، شما باید دو درایه را با هم تعویض کنید، دو درایه را خنثی کنید، و تمامی درایه ها را بر تفاضل بین حاصلضرب متقابل درایه ها، تقسیم کنید. ممکن است به نظر پیچیده آید، اما ریاضی آن واقعاً شسته و رفته و شیرین می باشد، و این فرآیند بسیار سریع تر از فرآیند عمومی یافتن معکوس ماتریس ها می باشد.
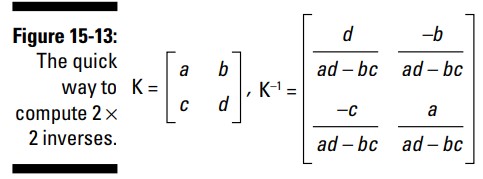
به عنوان مثال، برای یافتن معکوس ماتریس \(Z\) با استفاده از روش \(2\times2\) ، همانطور که در شکل 14-15 می بینید، دو درایۀ \(5\) و \(11\) را با یکدیگر تعویض می کنید، \(6\) را به \(-6\) و \(9\) را به \(-9\) تغییر می دهید، و آنها را بر تفاضل بین دو حاصلضرب متقابل، تقسیم می کنید ـــ \((5 \cdot 11) - (6 \cdot 9) = 55 -54 =1\) . ترتیبی که تفریق را انجام می دهید مهم است. همانطور که می توانید ببینید، تقسیم کردن هر درایه بر \(1\) مقدار آن درایه را تغییر نمی دهد.
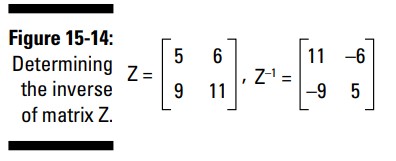

همچنین در جبر چیزی با نام وارون ضربی (multiplicative inverse) ـــ به آن معکوس ضربی نیز گفته می شود ـــ وجود دارد. وارون ضربی به شما عدد یک را می دهد. به عنوان مثال، وارون ضربیِ عدد \(2\) برابر با \({1\over2}\) می باشد.
جمع کردن یا ضرب کردن در معکوس ها همواره به شما عضو خنثی (identity element) را نتیجه می دهد. قبل از آنکه بتوانید معکوس ماتریس ها را پیدا کنید، نیاز دارید تا همانی ها (identities) را درک کنید، بنابراین جزئیات مربوط به همانی ها را در اینجا پوشش داده ام.
عضو خنثی در جمع (additive identity)
شما می توانید عدد صفر را با عنوان عضو خنثی در جمع برچسب گذاری کنید، زیرا افزودن صفر به یک عدد، به آن عدد امکان می دهد تا هویت (identity) خودش را حفظ کند. عضو خنثی در جمع، برای ماتریس ها برابر با ماتریس صفر (zero matrix) می باشد. هنگامی که یک ماتریس صفر را به هر ماتریس دیگری با ابعاد برابر، اضافه می کنید، ماتریس اصلی تغییری نمی کند.
یادتان باشد: تشخیص دادن ماتریس های معکوس مربوط به عملیات جمع، و همچنین ایجاد آنها، آسان می باشد. قرینۀ یک ماتریس، ماتریس دیگری با همان ابعاد می باشد، با این تفاوت که در ماتریس قرینه، علامت درایه ها متفاوت می باشد. هنگامی که یک ماتریس و قرینۀ آن را با یکدیگر جمع کنید، حاصلجمع تمامی درایه های متناظر آنها، همگی صفر خواهند شد. شکل 10-15 به شما نشان می دهد که چگونه حاصلجمع دو ماتریس صفر می گردد.
تمامی ماتریس ها دارای قرینه می باشند ـــ فرقی نمی کند ابعاد آن ماتریس چه باشد. در مورد وارون ضربیِ ماتریس ها قضیه اینطور نیست. برخی از ماتریس ها دارای وارون ضربی می باشند و برخی دیگر خیر. در ادامه در این رابطه بیشتر خواهید دانست.
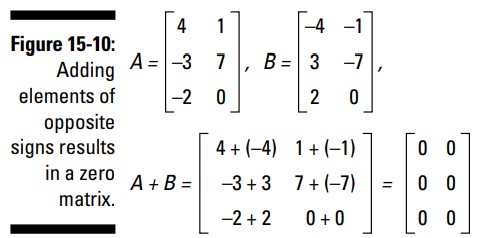
وارون ضربی (multiplicative inverse)
شما می توانید عدد یک را به عنوان عضو خنثی ضربی (multiplicative identity) برچسب گذاری کنید، زیرا ضرب کردن یک عدد در یک، مقدار آن را تغییر نمی دهد ـــ هویتش را حفظ می کند.
یادتان باشد: ماتریس ها دارای عضو خنثی در جمع می باشند که چیزی به جز صفر نیست، اما عضو خنثی ضربی (همانی ضربی) برای ماتریس ها، اندکی خاص تر می باشد. همانی ضربی برای یک ماتریس یک ماتریس مربعی می باشد، و در این ماتریس مربعی مجموعه ای از یک ها به شکل مورب قرار دارند؛ بقیۀ درایه های این ماتریس، صفر می باشند. این نظم و ترتیب اطمینان می دهد، وقتیکه هر ماتریسی را در یک همانی ضربی، ضرب نمایید، ماتریس اصلی تغییری نکند. شکل 11-15 فرآیند ضرب کردن دو ماتریس در همانی هایشان را نشان می دهد. قانون ضرب ماتریس ها در اینجا نیز وجود دارد: تعداد ستونها در ماتریس اول باید با تعداد سطرها در ماتریس دوم، برابر باشند.

شبیه همانی ضربی در یک ماتریس، وارون ضربی یک ماتریس به اندازۀ آن انطباق پذیر نیست. هنگامی که دو ماتریس را در یکدیگر ضرب می کنید، ضرب و جمع های فراوانی را صورت می دهید، و تغییرات زیادی را در ابعاد مشاهده خواهید کرد. به این دلیل، ماتریس ها و معکوس های ضربی آنها، همواره ماتریس های مربعی می باشند؛ ماتریس های غیرمربعی دارای وارون ضربی نمی باشند.
قوانین جبر: اگر ماتریس \(A\) و ماتریس \(A^{-1}\) وارون ضربیِ یکدیگر باشند، \(A \cdot A^{-1} = I\) ، و \(A^{-1} \cdot A = I\) . بالانویس \(-1\) بر روی ماتریس \(A\) آن را به عنوان وارون ضربیِ ماتریس \(A\) تعریف می کند. همچنین حرف بزرگ \(I\) نشان دهندۀ ماتریس همانیِ مرتبط با این ماتریس می باشد ـــ با ابعاد \(2 \times 2\) ، \(3 \times 3\) ، \(4 \times 4\) ، و به همین ترتیب.
در شکل 12-15 ، من ماتریس \(B\) و وارون آن \(B^{-1}\) را در یکدیگر ضرب نموده ام، سپس با تغییر دادن ترتیب آنها دوباره ضرب را تکرار کرده ام؛ نتیجۀ این فرآیند در هر دو بار برابر با ماتریس همانی شده است.
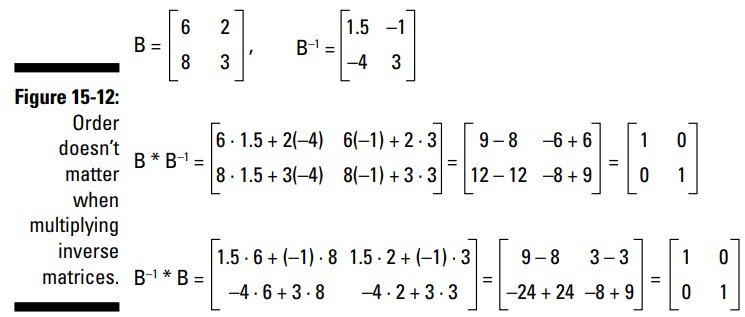
همۀ ماتریس های مربعی دارای معکوس نمی باشند. اما در مورد آنهایی که دارای معکوس ضربی هستند، شما روشی برای یافتن معکوس ضربی آن ماتریس ها دارید. شما همیشه قبل از شروع کار نمی دانید که آیا ماتریس مربوطه دارای معکوس هست یا نه، اما همچنانکه وارد فرآیند می شوید موضوع برای شما آشکار می گردد. اولین فرآیند یا الگوریتم (algorithm) ـــ الگوریتم یک فرآیند یا روال می باشد که نتیجه ای را تولید می کند ـــ که شما می توانید از آن برای ماتریس هایی در هر اندازه استفاده کنید، در ادامه آمده است. همچنین در مورد ماتریس های \(2 \times 2\) یک روش خاص وجود دارد که در ادامه به آن هم خواهیم پرداخت.
تعیین معکوس برای ماتریسی با هر ابعاد
یادتان باشد: روش عمومی برای یافتن معکوس یک ماتریس شامل نوشتن ماتریس، وارد کردن یک ماتریس همانی درون آن، و سپس تبدیل کردن ماتریس اصلی به ماتریس همانی می باشد.
برای حل کردن جهت یافتن معکوس یک ماتریس، این مراحل را دنبال کنید:
-
یک ماتریس بزرگ بسازید ـــ شامل ماتریس اصلی که می خواهید معکوسش را بیابید و یک ماتریس همانی با همان ابعاد ـــ ماتریس همانی در سمت راست ماتریس اصلی باشد.
-
عملیات های سطری را آنقدر انجام بدهید تا ماتریس همانی موجود در سمت راست، به سمت چپ منتقل شود و جای ماتریس اصلی را بگیرد.
نیاز می باشد تا درایه ها مجموعه ای از یک ها را به صورت مورب نشان دهند، که صفرهایی در بالا و پایین آنها قرار داشته باشند. به محض تکمیل این مرحله، درایه های موجود در سمت راست، تبدیل به درایه های ماتریس معکوس می شوند.
به عنوان مثال، فرض کنید می خواهید ماتریس \(M\) را که در ادامه نشان داده شده است، برای یافتن معکوس آن حل کنید. ابتدا یک ماتریس همانی با ابعاد \(3 \times 3\) در سمت راست درایه های ماتریس \(M\) ایجاد می کنید. هدف اینست که درایه های موجود در سمت چپ را با عملیات های سطری به یک ماتریس همانی تبدیل کنید.
$$
M=
\begin{bmatrix}
1&2&4\\
-3&-5&-6\\
2&-3&-36\\
\end{bmatrix}
$$
$$
\begin{bmatrix}
1&2&4&1&0&0\\
-3&-5&-6&0&1&0\\
2&-3&-36&0&0&1\\
\end{bmatrix}
$$
این ماتریس همانی دارای مجموعه ای از یک ها به صورت مورب می باشد، که صفرها در پایین و بالای آنها قرار گرفته اند. اولین چیز برای ایجاد ماتریس همانی مد نظرتان اینست که در زیر عدد یک موجود در بالا و سمت چپ ماتریس، صفرهایی را بدست آورید. در اینجا عملیات سطری مورد نیاز برای رسیدن به این هدف را می بینید:
-
سطر \(1\) را در \(3\) ضرب کنید و نتیجه را در سطر \(2\) قرار دهید.
-
سطر \(1\) را در \(-2\) ضرب کنید و نتیجه را در سطر \(3\) قرار دهید.
در ادامه نتیجۀ این عملیات های سطری را می بینید. نمادهای موجود بر روی فلش ها که بین دو ماتریس قرار دارند، عملیات های سطری را برای شما توصیف می کنند.
$$
\begin{bmatrix}
1&2&4&1&0&0\\
-3&-5&-6&0&1&0\\
2&-3&-36&0&0&1\\
\end{bmatrix}
\underset{\overset{(-2)R_1+R_3=R_3}{\longrightarrow}}{\overset{(3)R_1+R_2=R_2}{\longrightarrow}}
\begin{bmatrix}
1&2&4&1&0&0\\
0&1&6&3&1&0\\
0&-7&-44&-2&0&1\\
\end{bmatrix}
$$
یادتان باشد: شما در ستون دوم و سطر دوم ماتریس حاصله یک \(1\) می بینید ـــ در امتداد خط موربی از یک ها که می خواهید. بدست آوردن عدد \(1\) در این موقعیت اتفاق خوبی است؛ البته همیشه به این شکل نیست. اگر در این موقعیت \(1\) قرار نمی گرفت، شما باید آن ردیف را بر آنچه که منجر می شد تا این درایه به \(1\) تبدیل شود، تقسیم می کردید.
حالا، در بالا و پایین این \(1\) نیاز به صفرهایی دارید، بنابراین این مراحل را دنبال می کنید:
-
سطر \(2\) را در \(-2\) ضرب می کنید و نتیجه را به سطر \(1\) می افزایید.
-
سطر \(2\) را در \(7\) ضرب می کنید و نتیجه را به سطر \(3\) می افزایید.
$$
\begin{bmatrix}
1&2&4&1&0&0\\
0&1&6&3&1&0\\
0&-7&-44&-2&0&1\\
\end{bmatrix}
\underset{\overset{(7)R_2+R_3=R_3}{\longrightarrow}}{\overset{(-2)R_2+R_1=R_1}{\longrightarrow}}
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&-2&19&7&1\\
\end{bmatrix}
$$
اکنون نیاز دارید تا درایۀ موجود در سطر سوم و ستون سوم از ماتریس را به \(1\) تبدیل کنید، بنابراین سطر مربوطه را در \(-0.5\) ضرب می کنید؛ این ضرب برابر با تقسیم کردن سطر مربوطه بر \(-2\) می باشد.
$$
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&-2&19&7&1\\
\end{bmatrix}
\overset{(-0.5)R_3=R_3}{\longrightarrow}
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
شما یک مجموعه عملیات سطری دیگر نیاز دارید تا صفرهای موجود در بالای آخرین \(1\) از مجموعه یک های مورب را بدست آورید:
-
سطر \(3\) را در \(8\) ضرب کنید و درایه های موجود در آن را به سطر \(1\) بیفزایید.
-
سطر \(3\) را در \(-6\) ضرب کنید و نتیجه را به سطر \(2\) بیفزایید.
اکنون یک ماتریس \(3 \times 3\) همانی در سمت چپ و یک ماتریس \(3 \times 3\) در سمت راست دارید . درایه های موجود در ماتریس سمت راست، ماتریس معکوس یعنی ماتریس \(M^{-1}\) را شکل می دهند. حاصلضرب ماتریس \(M\) و معکوس آن یعنی \(M^{-1}\) ، ماتریس همانی می شوند. در ادامه دو مرحلۀ آخر و پاسخ نهایی نشان داده شده اند.
$$
\begin{bmatrix}
1&0&-8&-5&-2&0\\
0&1&6&3&1&0\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
\underset{\overset{(-6)R_3+R_2=R_2}{\longrightarrow}}{\overset{(8)R_3+R_1=R_1}{\longrightarrow}}
\begin{bmatrix}
1&0&0&-81&-30&-4\\
0&1&0&60&22&3\\
0&0&1&-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
$$
M^{-1}=
\begin{bmatrix}
-81&-30&-4\\
60&22&3\\
-9.5&-3.5&-0.5\\
\end{bmatrix}
$$
تصویر زیر درست آزمایی پاسخ بدست آمده را نشان می دهد ـــ نشان می دهد که \(M \cdot M^{-1}\) برابر با ماتریس همانی می باشد:
$$
M \cdot M^{-1}=
\begin{bmatrix}
1&2&4\\
-3&-5&-6\\
2&-3&-36\\
\end{bmatrix}
\cdot
\begin{bmatrix}
-81&-30&-4\\
60&22&3\\
-9.5&-3.5&-0.5\\
\end{bmatrix}
=
\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&1\\
\end{bmatrix}
$$
نکته: اگر ماتریسی دارای معکوس نباشد این اتفاق می افتد: شما نمی توانید با استفاده از عملیات سطری یک ها را به شکل مورب بدست آورید. شما معمولاً در نتایج عملیات های سطری تان به سطری از صفرها می رسید. وجود یک سطر از صفرها به عنوان هشداری می باشد که ماتریس مربوطه معکوس ندارد.
روشی سریع و مهارت آمیز برای یافتن معکوس ماتریس \(2\times2\)
شما برای یافتن معکوس ماتریس های \(2\times2\) قانون خاصی را در اختیار دارید. برای پیاده سازی قانون یافتن معکوس ماتریس \(2\times2\) ، شما باید دو درایه را با هم تعویض کنید، دو درایه را خنثی کنید، و تمامی درایه ها را بر تفاضل بین حاصلضرب متقابل درایه ها، تقسیم کنید. ممکن است به نظر پیچیده آید، اما ریاضی آن واقعاً شسته و رفته و شیرین می باشد، و این فرآیند بسیار سریع تر از فرآیند عمومی یافتن معکوس ماتریس ها می باشد.
قوانین جبر: شکل 13-15 فرمول عمومی برای ماتریس های \(2\times2\) را به شما نشان می دهد. همانطور که در تصویر می توانید ببینید، درایه های موجود در سمت بالا و چپ، و سمت راست و پایین، با یکدیگر تعویض شده اند؛ درایه های موجود در سمت بالا و راست، و سمت چپ و پایین، خنثی شده اند (به علامت معکوس شان تغییر یافته اند)؛ و تمامی درایه ها بر دو نتیجۀ حاصلضرب متقابل و تفریق آنها، تقسیم شده اند.
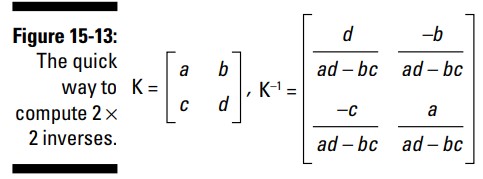
به عنوان مثال، برای یافتن معکوس ماتریس \(Z\) با استفاده از روش \(2\times2\) ، همانطور که در شکل 14-15 می بینید، دو درایۀ \(5\) و \(11\) را با یکدیگر تعویض می کنید، \(6\) را به \(-6\) و \(9\) را به \(-9\) تغییر می دهید، و آنها را بر تفاضل بین دو حاصلضرب متقابل، تقسیم می کنید ـــ \((5 \cdot 11) - (6 \cdot 9) = 55 -54 =1\) . ترتیبی که تفریق را انجام می دهید مهم است. همانطور که می توانید ببینید، تقسیم کردن هر درایه بر \(1\) مقدار آن درایه را تغییر نمی دهد.
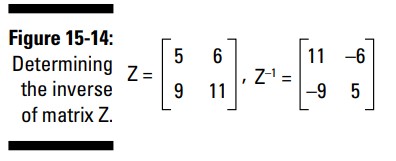
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: