خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
دنباله (Sequence)

یک دنباله (Sequence) لیستی از آیتم ها می باشد ـــ و از آنجا که این یک کتاب جبر است، دنباله هایی که شما در آن خواهید دید لیست هایی از اعداد را نشان خواهند داد. یک سری (series) مجموع اعداد موجود در یک لیست می باشد. این مفاهیم در نواحی بسیاری از زندگی بیرون می زنند. به عنوان مثال، شما می توانید لیستی از تعداد صندلی های موجود در هر ردیف از یک سینما، ایجاد کنید. در این لیست، شما می توانید اعدادی را برای یافتن مجموع تعداد صندلی ها اضافه کنید. شما تمایل دارید وضعیتهایی را ببینید که در آنها تعداد آیتم های موجودر در یک لیست، تصادفی نباشند؛ ترجیح شما اینست که اعداد یک الگو یا قاعده را دنبال کنند. شما می توانید الگوهای شکل گرفته با عناصر موجود در یک دنباله را با عبارات ریاضی شامل نمادها و عملیات ریاضی توصیف کنید. در این فصل، شما درخواهید یافت چگونه جملات موجود در یک دنباله را توصیف کنید و هرگاه که بخواهید بتوانید بدون هیچ آزار و اذیتی، به هر تعداد که بخواهید، اعضای جدیدی را به این دنباله اضافه کنید.

دنباله ای از رویدادها عبارت از دو یا چند رویداد است که در آنها یک آیتم یا رویداد، دیگری را ادامه می دهد، که آنهم دیگری را دنبال می کند، و به همین ترتیب. در ریاضی، یک دنباله لیستی از جملات (terms)، یا اعداد، می باشد، که با نوعی از قواعد ریاضی ایجاد شده اند. به عنوان مثال، \(\{3+4n\}\) می گوید که اعداد این دنباله باید با \(7\) آغاز شوند و در هر جمله دیگر \(4\) واحد افزایش پیدا کنند. اعداد موجود در این دنباله عبارت از \(7,11,15,...\) می باشند.
برای اینکه تعریف خاصتری از دنباله را داشته باشید، در اینجا تعریف رسمی دنباله را می آوریم: یک دنباله، یک تابع است که دامنۀ آن عبارت از اعداد صحیح مثبت \((1,2,3,...)\) می باشند. این واقعاً یک ویژگی زیبا می باشد ـــ سر و کار داشتن با اعداد مثبت صحیح. در ادامۀ این فصل چیزهای عالی و سودمند دیگری در مورد دنباله ها خواهید دانست.
یک سرنخ بزرگ برای نشان دادن اینکه شما با یک دنباله سر و کار دارید، آکولادها \(\{\}\) می باشند. مانند \(\{7,10,13,16,19,...\}\) یا \(\{a_n\}\) . آکولادها نشان می دهند که شما لیستی از آیتم ها را دارید، که به آنها جملات (terms) گفته می شود؛ معمولاً این جملات با ویرگول ها (comma) از یکدیگر جدا می شوند. جملۀ \(a_n\) نمادِ قاعده ای است که نشان دهندۀ یک دنبالۀ خاص می باشد. هنگام نشان دادن یک دنباله، شما می توانید جملات موجود در دنباله را لیست کنید، جملات کافی برای ایجاد یک الگو را نشان دهید، یا می توانید قاعده ای را که جملات را می سازد ارائه بدهید.
به عنوان مثال، اگر نماد \(\{2n+1\}\) را ببینید، خواهید دانست که دنبالۀ مربوطه عبارت از جملات \(\{3, 5, 7, 9, 11, 13, ...\}\) می باشد. \(2n+1\) قاعده ای (rule) است که این دنباله را در زمانیکه شما تمامی اعداد صحیح مثبت را به جای \(n\) وارد می کنید، می سازد. هنگامیکه \(n=1\) است، \(2(1)+1=3\) ؛ هنگامیکه \(n=2\) ، \(2(2)+1=5\) ؛ و به همین ترتیب. دامنۀ این دنباله تمامی اعداد صحیح مثبت می باشد، بنابراین این فرآیند به سادگی \(1,2,3\) می باشد.
یک عملیات ریاضی که در بسیاری از دنباله ها آن را خواهید دید، فاکتوریل (factorial) می باشد. نماد عملیات فاکتوریل یک علامت تعجب \((!)\) است.
هنگام انجام یک فاکتوریل، عدد مربوطه را که می خواهید فاکتوریلش را بدست آورید در هر عدد صحیح مثبت کوچکتر از آن عدد، ضرب می کنید.
به عنوان مثال، \(6!= 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\) ، و \(9!=9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=362,880\) .
خوب، اگر \(\{c_n\}=\{n!-n\}\) ، شما آن را به این شکل می نویسید:
$$
c_1=1!-1=1-1=0 \\[2ex]
c_2=2!-2=2 \cdot 1-2=0 \\[2ex]
c_3=3!-3=3 \cdot 2 \cdot 1-3=6-3=3 \\[2ex]
...
$$
شما جملات موجود در این دنباله را به شکل \(\{0,0,3,20,...\}\) می نویسید.
یکی از انواع خاص دنباله ها، دنبالۀ متناوب (alternating sequence) می باشد. یک دنبالۀ متناوب دارای جملاتی می باشد که تا ابد به صورت متناوب علامتشان از مثبت به منفی و سپس دوباره به مثبت تغییر می کند و به همین ترتیب این تغییر متناوب (یکی در میان) علامتها، ادامه می یابد. یک دنبالۀ متناوب دارای ضریبی از \(-1\) می باشد، که به توانهایی همچون \(n\) ، \(n-1\)، و یا \(n+1\) رسیده است. افزودن توانها، که به شمارۀ جمله بستگی دارد، به \(-1\) منجر می شود تا جملات به صورت متناوب علامتشان تغییر کند، زیرا اعداد صحیح مثبت بین اعداد زوج و فرد در تناوبند. توانهای زوج از \(-1\) برابر با \(+1\) و توانهای فرد از \(-1\) برابر با \(-1\) خواهند بود.
به عنوان مثال، این دنباله متناوب است: \(\{(-1)^n2(n+3)\}=\{-8,10,-12,14,...\}\)
$$
a_1=(-1)^1 2(1+3)=-1 \cdot 2(4)=-8 \\[2ex]
a_2=(-1)^2 2(2+3)=-1 \cdot 2(5)=10 \\[2ex]
a_3=(-1)^3 2(3+3)=-1 \cdot 2(6)=-12 \\[2ex]
...
$$
در اینجا مثالی از یک دنبالۀ متناوب که دارای یک کسر از فاکتوریل می باشد، داریم. چهار جملۀ اول این دنباله نیز در ادامه آورده شده اند:
$$
\biggl\{ (-1)^n \frac{(n+1)!}{n} \biggr\} \\[4ex]
a_1 = (-1)^1 \frac{(1+1)!}{1} = -1[{2! \over 1}] = -1[{2 \over 1}] = -2 \\[4ex]
a_2 = (-1)^2 \frac{(2+1)!}{2} = +1[{3! \over 2}] = 1[{6 \over 2}] = 3 \\[4ex]
a_3 = (-1)^3 \frac{(3+1)!}{3} = -1[{4! \over 3}] = -1[{24 \over 3}] = -8 \\[4ex]
a_4 = (-1)^4 \frac{(4+1)!}{4} = +1[{5! \over 4}] = 1[{120 \over 4}] = 30 \\[4ex]
...
$$
بنابراین، این دنباله عبارت است از \(\{-2,3,-8,30,...\}\)
شما می توانید ببینید چگونه قدر مطلق جملات بزرگ و بزرگتر می شوند، و همینطور علامت جملات نیز به صورت متناوب تغییر می کنند.
لیست جملات موجود در یک دنباله ممکن است یک الگوی واضح را نشان بدهند یا خیر. البته، اگر شما قاعدۀ تابع را داشته باشید ـــ قاعده ای که به شما می گوید چگونه تمامی جملات موجود در دنباله را بسازید ـــ راهنمای بزرگی در مورد الگوی جملات در اختیار خواهید داشت. اگر این قاعده را در اختیار داشته باشید، همواره می توانید جملات یک دنباله را لیست کنید، و همینطور معمولاً اگر به تعداد کافی جملاتی را در دنباله داشته باشید می توانید از روی روابط بین آنها ، به الگوی آن پی ببرید.
الگوهایی که شما می توانید بدنبالشان باشید، می توانند ساده یا پیچیده باشند:
هنگامی که ناگزیر به کشف یک الگو و نوشتن یک قاعده برای یک دنباله از اعداد هستید، می توانید به لیست احتمالات خودتان مراجعه کنید ـــ مواردی که ذکر کردم و بقیه ـــ و بررسی کنید که کدام نوع از قوانین در آنجا کاربرد دارد.
سریعترین و ساده ترین الگو برای یافتن، یک تفاضل عمومی بین جملات را نشان می دهد. تفاضل بین دو عدد، نتیجۀ تفریق آنها می باشد. شما معمولاً به سادگی می توانید با بررسی بگویید چه زمانی دنباله ای از این نوع دارید ـــ ببینید اعداد دنباله بر روی خط اعداد با چه فاصله ای از یکدیگر قرار گرفته اند.
سه دنباله ای که در ادامه آمده اند دارای یک چیز مشترک می باشند: جملات موجود در این دنباله ها دارای اولین تفاضل مشترک، دومین تفاضل مشترک، یا سومین تفاضل مشترک می باشند.
هنگامیکه اولین تفاضل (first difference) بین جملات یک دنباله عدد ثابتی باشد، قاعده ای که جملات را تعیین می کند، معمولاً یک عبارت خطی می باشد (یک عبارت خطی دارای توانی از \(1\) بر روی \(n\) می باشد). به عنوان مثال، دنبالۀ اعداد \(\{2, 7, 12, 17, 22, 27, ...\}\) عبارت از جملاتی می باشد که دارای تفاضل مشترک \(5\) می باشند. قاعدۀ این دنباله \(\{5n-3\}\) می باشد. شما از ضریب \(5\) استفاده می کنید تا جملات موجود در این دنباله هر کدام \(5\) واحد بزرگتر از جملۀ قبلی اش باشد. دلیل اینکه \(3\) را از آن تفریق می کنید اینست که هنگامی که \(n\) را با \(1\) جایگزین می کنید، به عدد خیلی بزرگی می رسید؛ شما می خواهید که این دنباله با عدد \(2\) آغاز گردد، بنابراین \(3\) را از اولین مضرب تفریق می کنید. دنباله هایی دارای اولین تفاضل مشترک، دنباله های حسابی (arithmetic sequences) نامیده می شوند (در ادامۀ همین فصل جزئیات بیشتری از این نوع دنباله ها را مطرح خواهم نمود).
هنگامیکه دومین تفاضل (Second difference) از جملات موجود در یک دنباله مقدار ثابتی، همچون \(2\) باشد، قاعدۀ آن دنباله معمولاً درجۀ دوم (quadratic) می باشد ـــ شامل جملۀ \(n^2\) می باشد. به عنوان مثال، دنبالۀ اعداد \(\{–2, 1, 6, 13, 22, 33, 46, ...\}\) ، عبارت از جملاتی می باشند که دارای دومین تفاضل مشترک \(2\) می باشند. اولین تفاضل مشترک بین جملات این دنباله هر بار \(2\) واحد افزایش می یابد:
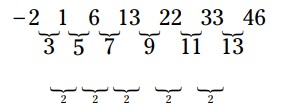
قاعده ای که برای ایجاد این دنباله استفاده می شود عبارت از \(\{n^2-3\}\) می باشد.
دنبالۀ \(\{0, 6, 24, 60, 120, 210, 336, ...\}\) یک سومین تفاضل مشترک (Third difference) از \(6\) را نشان می دهد. در طرح زیر، می توانید ببینید که ردیف زیر دنباله ها اولین تفاضل را نشان می دهد؛ در زیر اولین تفاضل ها، دومین تفاضل ها قرار دارند؛ و در پایان، ردیف سوم شامل سومین تفاضل ها می باشد:
قاعدۀ این دنباله \(\{n^3-n\}\) می باشد، که شامل یک جملۀ مکعبی است.
برخی از دنباله ها قوانین نسبتاً آشکاری دارند که جملات آنها را می سازند، زیرا هر جمله مضرب یا توانی از برخی مقادیر ثابت می باشد. به عنوان مثال، دنبالۀ \(\{3, 6, 9, 12, 15, 18, ...\}\) شامل مضربهایی از \(3\) می باشد، و قاعدۀ آن \(\{3n\}\) است.
اما اگر این دنباله با \(21\) آغاز شود چه می شود؟ قاعدۀ دنبالۀ \(\{21, 24, 27, 30, 33,36, ...\}\) چیست؟ همۀ این جملات مضربی از \(3\) می باشند، اما \(\{3n\}\) درست کار نخواهد کرد، زیرا شما باید با \(n=1\) آغاز کنید. یادتان باشد، دامنه یا مقادیر ورودی یک دنباله از اعداد صحیح مثبت ـــ \(1,2,3,...\) ـــ تشکیل می شوند، بنابراین شما نمی توانید چیزی کوچکتر از \(1\) را استفاده کنید.
دنبالۀ \(\biggl\{1,-{1\over2},{1\over3},-{1\over4},{1\over5},-{1\over6},... \biggr\}\) دارای دو ویژگی جالب می باشد: جملات دارای علامت متناوب هستند، و کسرها دارای اعداد صحیح مثبت در مخرجشان می باشند. برای نوشتن قاعدۀ این دنباله، این دو ویژگی را مد نظر قرار دهید. علامتهای متناوب به توانی از \(-1\) اشاره می کنند. اولین، سومین، پنجمین، و تمامی جملات فرد، مثبت می باشند، بنابراین فاکتور \(-1\) را به توان \(n+1\) می رسانید تا آن توانها و جملات را مثبت سازید. در مورد کسرها، شما می توانید \(n\) ، یعنی شمارۀ جملات را، در مخرج کسر قرار دهید. بنابراین، قاعدۀ این دنباله به شرح زیر می باشد:
$$
\biggl \{(-1)^{n+1} {1\over n} \biggr \} = \biggl \{ \frac{(-1)^{n+1}}{n} \biggr \}
$$
دنباله های دیگری هستند که می توانند دارای جملاتی باشند که همگی توانی از عدد یکسانی می باشد. این نوع دنباله ها را دنباله های هندسی (geometric sequences) می نامند (در ادامۀ همین فصل جزئیات بیشتری از دنباله های هندسی را با شما در میان خواهم گذاشت). یک مثال از دنباله های هندسی \(\{2, 4, 8, 16, 32, 64, 128, ...\}\) می باشد. شما می توانید ببینید که این جملات همگی توانی از \(2\) می باشند.

درک اصطلاحات فنیِ دنباله ها
دنباله ای از رویدادها عبارت از دو یا چند رویداد است که در آنها یک آیتم یا رویداد، دیگری را ادامه می دهد، که آنهم دیگری را دنبال می کند، و به همین ترتیب. در ریاضی، یک دنباله لیستی از جملات (terms)، یا اعداد، می باشد، که با نوعی از قواعد ریاضی ایجاد شده اند. به عنوان مثال، \(\{3+4n\}\) می گوید که اعداد این دنباله باید با \(7\) آغاز شوند و در هر جمله دیگر \(4\) واحد افزایش پیدا کنند. اعداد موجود در این دنباله عبارت از \(7,11,15,...\) می باشند.
برای اینکه تعریف خاصتری از دنباله را داشته باشید، در اینجا تعریف رسمی دنباله را می آوریم: یک دنباله، یک تابع است که دامنۀ آن عبارت از اعداد صحیح مثبت \((1,2,3,...)\) می باشند. این واقعاً یک ویژگی زیبا می باشد ـــ سر و کار داشتن با اعداد مثبت صحیح. در ادامۀ این فصل چیزهای عالی و سودمند دیگری در مورد دنباله ها خواهید دانست.
استفاده از نماد دنباله
یک سرنخ بزرگ برای نشان دادن اینکه شما با یک دنباله سر و کار دارید، آکولادها \(\{\}\) می باشند. مانند \(\{7,10,13,16,19,...\}\) یا \(\{a_n\}\) . آکولادها نشان می دهند که شما لیستی از آیتم ها را دارید، که به آنها جملات (terms) گفته می شود؛ معمولاً این جملات با ویرگول ها (comma) از یکدیگر جدا می شوند. جملۀ \(a_n\) نمادِ قاعده ای است که نشان دهندۀ یک دنبالۀ خاص می باشد. هنگام نشان دادن یک دنباله، شما می توانید جملات موجود در دنباله را لیست کنید، جملات کافی برای ایجاد یک الگو را نشان دهید، یا می توانید قاعده ای را که جملات را می سازد ارائه بدهید.
به عنوان مثال، اگر نماد \(\{2n+1\}\) را ببینید، خواهید دانست که دنبالۀ مربوطه عبارت از جملات \(\{3, 5, 7, 9, 11, 13, ...\}\) می باشد. \(2n+1\) قاعده ای (rule) است که این دنباله را در زمانیکه شما تمامی اعداد صحیح مثبت را به جای \(n\) وارد می کنید، می سازد. هنگامیکه \(n=1\) است، \(2(1)+1=3\) ؛ هنگامیکه \(n=2\) ، \(2(2)+1=5\) ؛ و به همین ترتیب. دامنۀ این دنباله تمامی اعداد صحیح مثبت می باشد، بنابراین این فرآیند به سادگی \(1,2,3\) می باشد.
توجه: از آنجا که جملات موجود در یک دنباله به اعداد صحیح مثبت متصل هستند، شما می توانید با لیست اعداد صحیح به موقعیت آنها در دنباله اشاره کنید. به عنوان مثال، اگر قاعدۀ یک دنباله \(\{a_n\}\) باشد، جملات موجود در این دنباله به این شکل نامگذاری می شوند: \(a_1,a_2,a_3,a_4,...\) . این سازماندهی زیبا و منظم، شما را قادر می سازد تا دهمین جملۀ دنبالۀ \(\{a_n\}=\{n^2-1\}\) را با نوشتن \(a_{10}=10^2-1=99\) درخواست کنید. شما برای رسیدن به دهمین جمله، نیازی نخواهید داشت تا نه جملۀ اول را بنویسید. نماد دنباله یک صرفه جویی خوب در زمان است!
فاکتوریل ها در دنباله ها
یک عملیات ریاضی که در بسیاری از دنباله ها آن را خواهید دید، فاکتوریل (factorial) می باشد. نماد عملیات فاکتوریل یک علامت تعجب \((!)\) است.
قوانین جبر: فرمول فاکتوریل در یک دنباله به این شکل می باشد:
$$ n!=n(n-1)(n-2)(n-3) ... 3 \cdot 2 \cdot 1 $$
$$ n!=n(n-1)(n-2)(n-3) ... 3 \cdot 2 \cdot 1 $$
هنگام انجام یک فاکتوریل، عدد مربوطه را که می خواهید فاکتوریلش را بدست آورید در هر عدد صحیح مثبت کوچکتر از آن عدد، ضرب می کنید.
به عنوان مثال، \(6!= 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\) ، و \(9!=9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=362,880\) .
توجه: در مورد \(0!\) یک قانون خاص وجود دارد. و آن اینکه \(0!=1\) می باشد. چی؟ چطور ممکن است؟ خوب، ممکن شده است. هرچند این مقدار با قانون فاکتوریل جور در نمی آید، اما ریاضیدانان آن را به عنوان یک قانون پذیرفته اند. ریاضیدانان دریافته اند که تخصیص دادن مقدار \(1\) برای \(0!\) ، منجر می شود تا همه چیزهایی که با فاکتوریل درگیر هستند، بهتر کار کنند. (دلیل اینکه شما به قانون \(0!\) نیاز دارید، در فصل 17 برایتان واضحتر خواهد شد. فعلاً به این راضی باشید که از این قانون برای نوشتن جملات در دنباله ها استفاده کنید.)
خوب، اگر \(\{c_n\}=\{n!-n\}\) ، شما آن را به این شکل می نویسید:
$$
c_1=1!-1=1-1=0 \\[2ex]
c_2=2!-2=2 \cdot 1-2=0 \\[2ex]
c_3=3!-3=3 \cdot 2 \cdot 1-3=6-3=3 \\[2ex]
...
$$
شما جملات موجود در این دنباله را به شکل \(\{0,0,3,20,...\}\) می نویسید.
الگوهای متناوب دنباله ای
یکی از انواع خاص دنباله ها، دنبالۀ متناوب (alternating sequence) می باشد. یک دنبالۀ متناوب دارای جملاتی می باشد که تا ابد به صورت متناوب علامتشان از مثبت به منفی و سپس دوباره به مثبت تغییر می کند و به همین ترتیب این تغییر متناوب (یکی در میان) علامتها، ادامه می یابد. یک دنبالۀ متناوب دارای ضریبی از \(-1\) می باشد، که به توانهایی همچون \(n\) ، \(n-1\)، و یا \(n+1\) رسیده است. افزودن توانها، که به شمارۀ جمله بستگی دارد، به \(-1\) منجر می شود تا جملات به صورت متناوب علامتشان تغییر کند، زیرا اعداد صحیح مثبت بین اعداد زوج و فرد در تناوبند. توانهای زوج از \(-1\) برابر با \(+1\) و توانهای فرد از \(-1\) برابر با \(-1\) خواهند بود.
به عنوان مثال، این دنباله متناوب است: \(\{(-1)^n2(n+3)\}=\{-8,10,-12,14,...\}\)
$$
a_1=(-1)^1 2(1+3)=-1 \cdot 2(4)=-8 \\[2ex]
a_2=(-1)^2 2(2+3)=-1 \cdot 2(5)=10 \\[2ex]
a_3=(-1)^3 2(3+3)=-1 \cdot 2(6)=-12 \\[2ex]
...
$$
در اینجا مثالی از یک دنبالۀ متناوب که دارای یک کسر از فاکتوریل می باشد، داریم. چهار جملۀ اول این دنباله نیز در ادامه آورده شده اند:
$$
\biggl\{ (-1)^n \frac{(n+1)!}{n} \biggr\} \\[4ex]
a_1 = (-1)^1 \frac{(1+1)!}{1} = -1[{2! \over 1}] = -1[{2 \over 1}] = -2 \\[4ex]
a_2 = (-1)^2 \frac{(2+1)!}{2} = +1[{3! \over 2}] = 1[{6 \over 2}] = 3 \\[4ex]
a_3 = (-1)^3 \frac{(3+1)!}{3} = -1[{4! \over 3}] = -1[{24 \over 3}] = -8 \\[4ex]
a_4 = (-1)^4 \frac{(4+1)!}{4} = +1[{5! \over 4}] = 1[{120 \over 4}] = 30 \\[4ex]
...
$$
بنابراین، این دنباله عبارت است از \(\{-2,3,-8,30,...\}\)
شما می توانید ببینید چگونه قدر مطلق جملات بزرگ و بزرگتر می شوند، و همینطور علامت جملات نیز به صورت متناوب تغییر می کنند.
جستجو برای یافتن الگوهای دنباله ها
لیست جملات موجود در یک دنباله ممکن است یک الگوی واضح را نشان بدهند یا خیر. البته، اگر شما قاعدۀ تابع را داشته باشید ـــ قاعده ای که به شما می گوید چگونه تمامی جملات موجود در دنباله را بسازید ـــ راهنمای بزرگی در مورد الگوی جملات در اختیار خواهید داشت. اگر این قاعده را در اختیار داشته باشید، همواره می توانید جملات یک دنباله را لیست کنید، و همینطور معمولاً اگر به تعداد کافی جملاتی را در دنباله داشته باشید می توانید از روی روابط بین آنها ، به الگوی آن پی ببرید.
الگوهایی که شما می توانید بدنبالشان باشید، می توانند ساده یا پیچیده باشند:
-
بین هر جمله یک تفاضل ثابت قرار دارد، به عنوان مثال در دنبالۀ \(4,9,14,19,...\) تفاضل بین هر دو جملۀ کنار هم \(5\) می باشد.
-
جملات توسط یک ضریب از یکدیگر جدا شده اند، به عنوان مثال ضرب کردن در \(5\) برای رسیدن به \(2,10,50,250,...\) .
-
الگویی درون الگویی دیگر قرار گرفته است، به عنوان مثال در دنبالۀ \(2,5,9,14,20,...\) تفاضل بین اعداد دنباله هر بار یک واحد افزایش پیدا می کند.
هنگامی که ناگزیر به کشف یک الگو و نوشتن یک قاعده برای یک دنباله از اعداد هستید، می توانید به لیست احتمالات خودتان مراجعه کنید ـــ مواردی که ذکر کردم و بقیه ـــ و بررسی کنید که کدام نوع از قوانین در آنجا کاربرد دارد.
تفاضل بین جملات
سریعترین و ساده ترین الگو برای یافتن، یک تفاضل عمومی بین جملات را نشان می دهد. تفاضل بین دو عدد، نتیجۀ تفریق آنها می باشد. شما معمولاً به سادگی می توانید با بررسی بگویید چه زمانی دنباله ای از این نوع دارید ـــ ببینید اعداد دنباله بر روی خط اعداد با چه فاصله ای از یکدیگر قرار گرفته اند.
نکته: هنگامی که بدنبال تفاضل ها در لیستی از اعداد هستید، مراقب باشید که همیشه در ترتیب یکسانی تفریق را انجام بدهید ـــ عدد مربوطه صرفاً منهای عدد موجود در سمت چپ آن می شود.
سه دنباله ای که در ادامه آمده اند دارای یک چیز مشترک می باشند: جملات موجود در این دنباله ها دارای اولین تفاضل مشترک، دومین تفاضل مشترک، یا سومین تفاضل مشترک می باشند.
اولین تفاضل
هنگامیکه اولین تفاضل (first difference) بین جملات یک دنباله عدد ثابتی باشد، قاعده ای که جملات را تعیین می کند، معمولاً یک عبارت خطی می باشد (یک عبارت خطی دارای توانی از \(1\) بر روی \(n\) می باشد). به عنوان مثال، دنبالۀ اعداد \(\{2, 7, 12, 17, 22, 27, ...\}\) عبارت از جملاتی می باشد که دارای تفاضل مشترک \(5\) می باشند. قاعدۀ این دنباله \(\{5n-3\}\) می باشد. شما از ضریب \(5\) استفاده می کنید تا جملات موجود در این دنباله هر کدام \(5\) واحد بزرگتر از جملۀ قبلی اش باشد. دلیل اینکه \(3\) را از آن تفریق می کنید اینست که هنگامی که \(n\) را با \(1\) جایگزین می کنید، به عدد خیلی بزرگی می رسید؛ شما می خواهید که این دنباله با عدد \(2\) آغاز گردد، بنابراین \(3\) را از اولین مضرب تفریق می کنید. دنباله هایی دارای اولین تفاضل مشترک، دنباله های حسابی (arithmetic sequences) نامیده می شوند (در ادامۀ همین فصل جزئیات بیشتری از این نوع دنباله ها را مطرح خواهم نمود).
دومین تفاضل
هنگامیکه دومین تفاضل (Second difference) از جملات موجود در یک دنباله مقدار ثابتی، همچون \(2\) باشد، قاعدۀ آن دنباله معمولاً درجۀ دوم (quadratic) می باشد ـــ شامل جملۀ \(n^2\) می باشد. به عنوان مثال، دنبالۀ اعداد \(\{–2, 1, 6, 13, 22, 33, 46, ...\}\) ، عبارت از جملاتی می باشند که دارای دومین تفاضل مشترک \(2\) می باشند. اولین تفاضل مشترک بین جملات این دنباله هر بار \(2\) واحد افزایش می یابد:
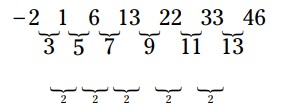
قاعده ای که برای ایجاد این دنباله استفاده می شود عبارت از \(\{n^2-3\}\) می باشد.
توجه: من نمی توانم یک روش سریع و آسان برای یافتن یک قاعده خاص را به شما بدهم، اما اگر شما بدانید که یک قاعده باید درجه دوم باشد، جایی برای آغاز کار دارید. شما می توانید سعی کنید تا اعداد \(1,2,3\) و به همین ترتیب را مربع سازید، و سپس بررسی کنید که چگونه با تفریق یا جمع کردن می توانید مربع ها را تنظیم کنید تا قاعدۀ آن دنباله برای شما آشکار گردد.
سومین تفاضل
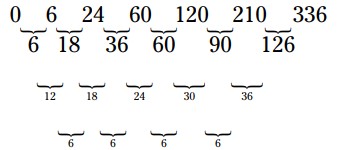
دنبالۀ \(\{0, 6, 24, 60, 120, 210, 336, ...\}\) یک سومین تفاضل مشترک (Third difference) از \(6\) را نشان می دهد. در طرح زیر، می توانید ببینید که ردیف زیر دنباله ها اولین تفاضل را نشان می دهد؛ در زیر اولین تفاضل ها، دومین تفاضل ها قرار دارند؛ و در پایان، ردیف سوم شامل سومین تفاضل ها می باشد:

قاعدۀ این دنباله \(\{n^3-n\}\) می باشد، که شامل یک جملۀ مکعبی است.
توجه: هنگامیکه به این جملات نگاه می کنید، قاعدۀ این دنباله الزاماً فوراً آشکار نمی شود. برای تعیین این قاعده مجبور هستید تا روش های مختلفی را بر روی جملات امتحان کنید تا به نتیجۀ مطلوب برسید. با جملۀ مکعب شده کار را آغاز کنید و سپس سعی کنید تا با جمع یا تفریق کردنِ مقادیر ثابت، به نتیجه برسید. اگر این روش جواب نداد، سعی کنید مقادیر مربع شده یا صرفاً ضرب شده، را از آن جمع یا تفریق کنید. به نوعی تصادفی به نظر می رسد، اما بدون استفاده از حسابان (calculus)، شما گزینه های محدودی را در اختیار دارید. ماشین حسابهای نموداری قابلیتی با نام پردازش منحنی (curvefitting) دارند که داده ها را دریافت می کند و قاعده ها را برای شما پیدا می کند، اما هنوز هم نیاز دارید تا تعیین کنید کدام نوع از قاعده ها (کدام توانها) را می خواهید.
مضرب ها و توان ها
برخی از دنباله ها قوانین نسبتاً آشکاری دارند که جملات آنها را می سازند، زیرا هر جمله مضرب یا توانی از برخی مقادیر ثابت می باشد. به عنوان مثال، دنبالۀ \(\{3, 6, 9, 12, 15, 18, ...\}\) شامل مضربهایی از \(3\) می باشد، و قاعدۀ آن \(\{3n\}\) است.
اما اگر این دنباله با \(21\) آغاز شود چه می شود؟ قاعدۀ دنبالۀ \(\{21, 24, 27, 30, 33,36, ...\}\) چیست؟ همۀ این جملات مضربی از \(3\) می باشند، اما \(\{3n\}\) درست کار نخواهد کرد، زیرا شما باید با \(n=1\) آغاز کنید. یادتان باشد، دامنه یا مقادیر ورودی یک دنباله از اعداد صحیح مثبت ـــ \(1,2,3,...\) ـــ تشکیل می شوند، بنابراین شما نمی توانید چیزی کوچکتر از \(1\) را استفاده کنید.
توجه: روشی که با آن دنباله هایی با اعداد کوچکتر را آغاز می کنید اینست که یک مقدار ثابت را به \(n\) بیفزایید (که شبیه یک شمارنده می باشد). عدد \(21\) برابر با \(3 \cdot 7\) می باشد، بنابراین \(6\) را به \(n\) بیفزایید \((1+6=7)\) تا قاعده را شکل دهید \(\{3(n+6)\}\) .
دنبالۀ \(\biggl\{1,-{1\over2},{1\over3},-{1\over4},{1\over5},-{1\over6},... \biggr\}\) دارای دو ویژگی جالب می باشد: جملات دارای علامت متناوب هستند، و کسرها دارای اعداد صحیح مثبت در مخرجشان می باشند. برای نوشتن قاعدۀ این دنباله، این دو ویژگی را مد نظر قرار دهید. علامتهای متناوب به توانی از \(-1\) اشاره می کنند. اولین، سومین، پنجمین، و تمامی جملات فرد، مثبت می باشند، بنابراین فاکتور \(-1\) را به توان \(n+1\) می رسانید تا آن توانها و جملات را مثبت سازید. در مورد کسرها، شما می توانید \(n\) ، یعنی شمارۀ جملات را، در مخرج کسر قرار دهید. بنابراین، قاعدۀ این دنباله به شرح زیر می باشد:
$$
\biggl \{(-1)^{n+1} {1\over n} \biggr \} = \biggl \{ \frac{(-1)^{n+1}}{n} \biggr \}
$$
دنباله های دیگری هستند که می توانند دارای جملاتی باشند که همگی توانی از عدد یکسانی می باشد. این نوع دنباله ها را دنباله های هندسی (geometric sequences) می نامند (در ادامۀ همین فصل جزئیات بیشتری از دنباله های هندسی را با شما در میان خواهم گذاشت). یک مثال از دنباله های هندسی \(\{2, 4, 8, 16, 32, 64, 128, ...\}\) می باشد. شما می توانید ببینید که این جملات همگی توانی از \(2\) می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: