خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تنصیف و تثلیث پاره خطها و زوایا

در این بخش در مورد تنصیف (Bisection) و تثلیث (Trisection) صحبت خواهیم کرد. تنصیف از نصف کردن می آید و به معنای دو نیم کردن یک پاره خط یا زاویه می باشد. تثلیث که با کلمۀ مثلث شباهت دارد به معنای سه بخش کردن است، که آنهم مانند تنصیف هم در مورد پاره خطها و هم در مورد زوایا کاربرد دارد. هدف اصلی در اینجا اینست که بعد از اینکه با استفاده از تنصیف یا تثلیث یک پاره خط یا زاویه را به دو یا سه قسمت مساوی تقسیم نمودید، در پایان به بخشهایی همنهشت از آن پاره خط یا زاویه برسید. در فصل 5 خواهید دید که این دو عملیات در اثبات های هندسی سودمند خواهند بود.

تنصیف پاره خطها، و واژۀ نقطۀ میانی (midpoint) که به آن مرتبط است، و تثلیث پاره خطها، مفاهیم بسیار ساده ای هستند. (تعاریف اینها که در ادامه می آید به وفور در اثبات های هندسی مورد استفاده قرار می گیرند. فصل 4 را ببینید.)
در اینجا یک مسأله داریم که می توانید با استفاده از مثلث موجود در شکل 7-3 آن را امتحان کنید. با دانستن اینکه نیم خطهای \(\overrightarrow{AJ}\) و \(\overrightarrow{AZ}\)، \(\overline{BC}\) را تثلیث می کنند، طول \(\overline{BC}\) را تعیین کنید.
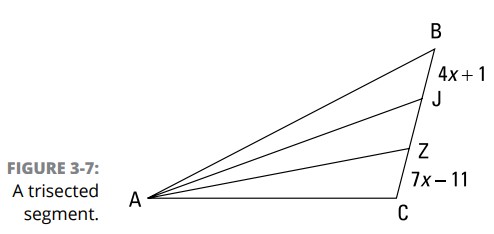
اوکی، در اینجا چگونگی حل این مسأله را می بینید: \(\overline{BC}\) تثلیث شده است، بنابراین به سه قسمت همنهشت تقسیم شده است؛ از اینرو، \(BJ=ZC\) . صرفاً اینها را برابر یکدیگر قرار دهید و معادله را برای یافتن \(x\) حل کنید:
$$
4x+1=7x-11 \\
12=3x \\
x=4
$$
اکنون \(4\) را در \(4x+1\) و \(7x-11\) جایگذاری کنید، که نتیجۀ \(17\) را برای هر پاره خط به شما می دهد. همچنین \(JZ\) نیز باید برابر با \(17\) باشد، بنابراین \(BC\) باید مجموع این سه پاره خط، یعنی \(3 \cdot 17\) یا \(51\) گردد. کافیه.
راستی، مراقب باشید این اشتباه رایج را مرتکب نشوید: فکر نکنید چون \(\overline{BC}\) تثلیث شده است، \(\angle{BAC}\) نیز باید الزاماً تثلیث شده باشد.
در این مسألۀ بخصوص، شما به احتمال زیاد در دام این خطای خطرناک بیفتید که من نیم خطهای \(\overrightarrow{AJ}\) و \(\overrightarrow{AZ}\) را دارم (به جای نقاط \(J\) و \(Z\)) که \(\overline{BC}\) را تثلیث کرده اند، و نیم خطها معمولاً زاویه ها را تثلیث می کنند. اما داده های این مسأله به تثلیث \(\overline{BC}\) اشاره دارند، و نه تثلیث \(\angle{BAC}\) ، و روشی که نیم خطها پاره خط \(\overline{BC}\) را تقسیم می کنند یک نتیجۀ مجزا و متفاوت از روشی که آنها \(\angle{BAC}\) را تقسیم می کنند، دارد.
سعی کنید تا این مسأله را حل کنید: در شکل 8-3، \(\overrightarrow{TP}\) روی \(\angle{STL}\) که برابر با \((12x-24)^{\circ}\) تنصیف را انجام می دهد؛ \(\overrightarrow{TL}\) روی \(\angle{PTI}\) که برابر با \((8x)^{\circ}\) می باشد، تنصیف را انجام می دهد. آیا روی \(\angle{STI}\) تثلیث انجام گرفته است، و اگر اینطور است اندازه های آن چیست؟
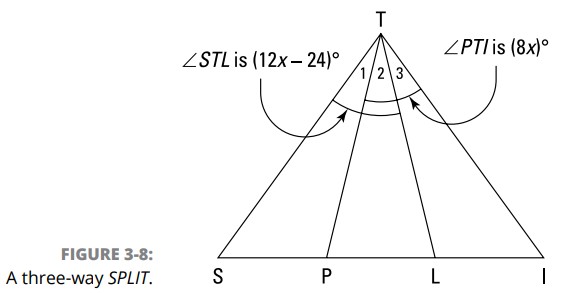
خیلی ساده است. ابتدا، بله \(\angle{STI}\) تثلیث شده است. شما این را از اینجا می دانید که \(\angle{STL}\) تنصیف شده است، بنابراین \(\angle{1}\) یاید با \(\angle{2}\) برابر باشد. و از آنجا که \(\angle{PTI}\) تنصیف شده است، \(\angle{2}\) با \(\angle{3}\) برابر می باشد. بنابراین هر سۀ این زاویه ها باید با هم برابر باشند، و این بدین معنا می باشد که \(\angle{STI}\) تثلیث شده است.
حالا به سراغ اندازۀ \(\angle{STI}\) می رویم. از آنجا که \(\angle{STL}\) ـــ که اندازه اش \((12x-24)^{\circ}\) می باشد ـــ تنصیف شده است، \(\angle{2}\) باید نصف این اندازه باشد، که می شود \((6x-12)^{\circ}\) . و از آنجا که \(\angle{PTI}\) تنصیف شده است، \(\angle{2}\) باید نصف اندازۀ \(\angle{PTI}\) نیز باشد ـــ که می شود نصف \((8x)^{\circ}\) ، یا \((4x)^{\circ}\) . از آنجا که \(\angle{2}\) هم با \((6x-12)^{\circ}\) و هم با \((4x)^{\circ}\) برابر می باشد، این دو عبارت را برابر یکدیگر قرار می دهید و معادلۀ بدست آمده را برای یافتن \(x\) حل می کنید:
$$
6x-12=4x \\
2x=12 \\
x=6
$$
سپس، کافیست \(6\) را در اندازه ها جایگذاری کنیم، اگر \(6\) را در \((4x)^{\circ}\) جایگذاری کنیم به \(4 \cdot 6\) یا \(24^{\circ}\) برای \(\angle{2}\) می رسیم. زاویۀ \(STI\) سه برابر آن می باشد، بنابراین می شود \(72^{\circ}\) . کافیه.
به عنوان مثال، در شکل 8-3 ، از آنجا که \(\angle{STI}\) تثلیث شده است، \(\overline{SI}\) قطعاً تثلیث نشده است. توجه داشته باشید که این معکوس هشداری است که در بخش قبلی در مورد تثلیث نیم خط ها گفتیم، که به شما گفته بودیم اگر یک ضلع از یک مثلث تثلیث گردد، آن زاویه تثلیث نشده است.

تنصیف و تثلیث پاره خطها
تنصیف پاره خطها، و واژۀ نقطۀ میانی (midpoint) که به آن مرتبط است، و تثلیث پاره خطها، مفاهیم بسیار ساده ای هستند. (تعاریف اینها که در ادامه می آید به وفور در اثبات های هندسی مورد استفاده قرار می گیرند. فصل 4 را ببینید.)
-
تنصیف پاره خط: یک نقطه، پاره خط، نیم خط، یا خط که یک پاره خط را به دو قسمت همنهشت تقسیم می کند، آن پاره خط را تنصیف می کند.
-
نقطۀ میانی: نقطه ای که یک پاره خط در آنجا تنصیف شده است، نقطۀ میانی نامیده می شود؛ نقطۀ میانی آن پاره خط را به دو قسمت همنهشت تقسیم می کند.
-
تثلیث پاره خط: دو چیز (دو نقطه، دو پاره خط، دو نیم خط، یا ترکیبی از اینها) که یک پاره خط را به سه قسمت همنشت تقسیم می کند، آن پاره خط را تثلیث کرده است. نقاط جدا شدن را نقاط تثلیث آن پاره خط (trisection points) می گویند.
در اینجا یک مسأله داریم که می توانید با استفاده از مثلث موجود در شکل 7-3 آن را امتحان کنید. با دانستن اینکه نیم خطهای \(\overrightarrow{AJ}\) و \(\overrightarrow{AZ}\)، \(\overline{BC}\) را تثلیث می کنند، طول \(\overline{BC}\) را تعیین کنید.

اوکی، در اینجا چگونگی حل این مسأله را می بینید: \(\overline{BC}\) تثلیث شده است، بنابراین به سه قسمت همنهشت تقسیم شده است؛ از اینرو، \(BJ=ZC\) . صرفاً اینها را برابر یکدیگر قرار دهید و معادله را برای یافتن \(x\) حل کنید:
$$
4x+1=7x-11 \\
12=3x \\
x=4
$$
اکنون \(4\) را در \(4x+1\) و \(7x-11\) جایگذاری کنید، که نتیجۀ \(17\) را برای هر پاره خط به شما می دهد. همچنین \(JZ\) نیز باید برابر با \(17\) باشد، بنابراین \(BC\) باید مجموع این سه پاره خط، یعنی \(3 \cdot 17\) یا \(51\) گردد. کافیه.
راستی، مراقب باشید این اشتباه رایج را مرتکب نشوید: فکر نکنید چون \(\overline{BC}\) تثلیث شده است، \(\angle{BAC}\) نیز باید الزاماً تثلیث شده باشد.
هشدار: اگر ضلعی از یک مثلث توسط نیم خطهایی از رأس مقایل آن تثلیث شده باشد، زاویۀ آن رأس نمی تواند تثلیث شده باشد. معمولاً اینطور به نظر می رسد که زاویۀ آن رأس تثلیث شده باشد، و اغلب هم به سه بخش تقریباً برابر تقسیم می گردد، اما این هرگز یک تثلیث دقیق نیست.
در این مسألۀ بخصوص، شما به احتمال زیاد در دام این خطای خطرناک بیفتید که من نیم خطهای \(\overrightarrow{AJ}\) و \(\overrightarrow{AZ}\) را دارم (به جای نقاط \(J\) و \(Z\)) که \(\overline{BC}\) را تثلیث کرده اند، و نیم خطها معمولاً زاویه ها را تثلیث می کنند. اما داده های این مسأله به تثلیث \(\overline{BC}\) اشاره دارند، و نه تثلیث \(\angle{BAC}\) ، و روشی که نیم خطها پاره خط \(\overline{BC}\) را تقسیم می کنند یک نتیجۀ مجزا و متفاوت از روشی که آنها \(\angle{BAC}\) را تقسیم می کنند، دارد.
تنصیف و تثلیث زاویه ها
خودتان را برای یک شوک واقعی آماده کنید: اصطلاحات تنصیف و تثلیث، در مورد زاویه ها همان معنی را می دهند که در مورد پاره خط ها دارند! (تعاریف آنها معمولاً در اثبات ها مورد استفاده قرار می گیرد. فصل 4 را بررسی کنید.)
-
تنصیف زاویه ها: یک نیمخط که یک زاویه را به دو قسمت همنهشت تقسیم می کند، آن را تنصیف می کند. این نیم خط منصف یا نیمساز زاویه (angle bisector) نامیده میشود.
-
تثلیث زاویه: دو نیم خط که زاویه ای را به سه قسمت همنشهت تقسیم می کنند، آن را تثلیث می کنند. این نیم خط ها را تثلیث ساز زاویه (angle trisectors) می نامند.
سعی کنید تا این مسأله را حل کنید: در شکل 8-3، \(\overrightarrow{TP}\) روی \(\angle{STL}\) که برابر با \((12x-24)^{\circ}\) تنصیف را انجام می دهد؛ \(\overrightarrow{TL}\) روی \(\angle{PTI}\) که برابر با \((8x)^{\circ}\) می باشد، تنصیف را انجام می دهد. آیا روی \(\angle{STI}\) تثلیث انجام گرفته است، و اگر اینطور است اندازه های آن چیست؟

خیلی ساده است. ابتدا، بله \(\angle{STI}\) تثلیث شده است. شما این را از اینجا می دانید که \(\angle{STL}\) تنصیف شده است، بنابراین \(\angle{1}\) یاید با \(\angle{2}\) برابر باشد. و از آنجا که \(\angle{PTI}\) تنصیف شده است، \(\angle{2}\) با \(\angle{3}\) برابر می باشد. بنابراین هر سۀ این زاویه ها باید با هم برابر باشند، و این بدین معنا می باشد که \(\angle{STI}\) تثلیث شده است.
حالا به سراغ اندازۀ \(\angle{STI}\) می رویم. از آنجا که \(\angle{STL}\) ـــ که اندازه اش \((12x-24)^{\circ}\) می باشد ـــ تنصیف شده است، \(\angle{2}\) باید نصف این اندازه باشد، که می شود \((6x-12)^{\circ}\) . و از آنجا که \(\angle{PTI}\) تنصیف شده است، \(\angle{2}\) باید نصف اندازۀ \(\angle{PTI}\) نیز باشد ـــ که می شود نصف \((8x)^{\circ}\) ، یا \((4x)^{\circ}\) . از آنجا که \(\angle{2}\) هم با \((6x-12)^{\circ}\) و هم با \((4x)^{\circ}\) برابر می باشد، این دو عبارت را برابر یکدیگر قرار می دهید و معادلۀ بدست آمده را برای یافتن \(x\) حل می کنید:
$$
6x-12=4x \\
2x=12 \\
x=6
$$
سپس، کافیست \(6\) را در اندازه ها جایگذاری کنیم، اگر \(6\) را در \((4x)^{\circ}\) جایگذاری کنیم به \(4 \cdot 6\) یا \(24^{\circ}\) برای \(\angle{2}\) می رسیم. زاویۀ \(STI\) سه برابر آن می باشد، بنابراین می شود \(72^{\circ}\) . کافیه.
هنگامی که نیم خطهایی یک زاویه از یک مثلث را تثلیث می کنند، ضلع مقابل آن مثلث هرگز با این نیم خط ها تثلیث نشده است.
به عنوان مثال، در شکل 8-3 ، از آنجا که \(\angle{STI}\) تثلیث شده است، \(\overline{SI}\) قطعاً تثلیث نشده است. توجه داشته باشید که این معکوس هشداری است که در بخش قبلی در مورد تثلیث نیم خط ها گفتیم، که به شما گفته بودیم اگر یک ضلع از یک مثلث تثلیث گردد، آن زاویه تثلیث نشده است.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: