خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مثلث های سه تایی فیثاغورثی

اگر هر دو عدد قدیمی را به عنوان دو ضلع یک مثلث قائم الزاویه استفاده کنید، قضیۀ فیثاغورث تقریباً همیشه مربع چیزی را به عنوان ضلع سوم به شما می دهد. به عنوان مثال، یک مثلث قائم الزاویه با ساق های \(5\) و \(6\) دارای وتر \(\sqrt{61}\) می باشد؛ اگر ساق ها \(3\) و \(8\) باشند، وتر برابر با \(\sqrt{73}\) می باشد؛ و اگر یکی از ساق ها \(6\) باشد و وتر برابر با \(9\) باشد، ساق دیگر به \(\sqrt{81-36}\) محاسبه می شود، که برابر با \(\sqrt{45}\) ، یا \(3\sqrt{5}\) می باشد.

یک مثلث چندتایی فیثاغورثی (Pythagorean triple triangle) یک مثلث قائم الزاویه می باشد که طول همۀ اضلاع آن اعداد کامل می باشند، مانند \(3\) ، \(4\) ، و \(5\)، یا \(5\) ، \(12\) ، و \(13\) . افراد تمایل دارند تا از این مثلث ها در مسائل استفاده کنند، زیرا شامل آن اعداد آزار دهندۀ زیر رادیکال نمی شوند. علیرغم اینکه بی نهایت از اینگونه مثلث ها وجود دارند، آنها بسیار نادر می باشند (مانند این واقعیت که مضربهای عدد \(100\) در بین سایر اعداد بسیار نادر هستند، حتی با وجود اینکه بی نهایت از این مضربها وجود دارند).
چهار مثلث اول از نوع سه تایی فیثاغورثی محبوبِ طراحانِ مسائل هندسی می باشند. این سه تایی ها ـــ مخصوصاً مورد اول و دوم در این لیست که در ادامه آمده است ـــ در تمامی کتابهای هندسی ظاهر شده اند. (نکته: دو عدد اول در هر مثلث سه تایی طول ساق ها می باشند، و عدد سوم، یعنی بزرگترین عدد، طول وتر می باشد).
خوب است این چهار مثلث محبوب را به خاطر بسپارید، تا بتوانید آنها را به سرعت در آزمون ها تشخیص دهید.
به عنوان جایگزینی برای شمارش گوسفندان در هنگام خواب، ممکن است بخواهید بدانید چندتا مثلث سه تایی فیثاغورثیِ دیگر را می توانید بدست آورید.
سه تایِ اول در لیست پیشین یک الگو را دنبال می کنند. به عنوان مثال، مثلث \(5-12-13\) را در نظر بگیرید. مربع عدد کوچکتر، ساق فرد (\(5^2=25\)) مجموع ساق های بزرگتر و وتر می باشد (\(12+13=25\)). و ساق بزرگتر و وتر همیشه اعداد متوالی هستند. این الگو به شما امکان می دهد تا به هر تعداد مثلث که می خواهید تولید کنید. کاری که باید انجام بدهید در اینجا آمده است:
در اینجا چند مثلث سه تایی فیثاغورثی بعدی، که این الگو را دنبال می کنند، می بینید:
این لیست بی پایان می باشد ـــ قادر است تا با بدترین نوع بیخوابی مقابله کند. و توجه داشته باشید که هر مثلث در این لیست کاهش ناپذیر (irreducible) می باشد؛ یعنی، مضربی از مثلث سه تایی فیثاغورثیِ کوچکتری نمی باشد (به عنوان مثال، در مقایسه با مثلث \(6-8-10\) ، که کاهش ناپذیر نمی باشد، زیرا دوبرابر شدۀ مثلث \(3-4-5\) است).
هنگامی که یک مثلث سه تایی فیثاغورثیِ جدید (مانند \(6-8-10\)) را با بزرگتر کردن یک مثلث سه تایی کوچکتر (\(3-4-5\)) می سازید، شما مثلث هایی با شکل دقیقاً یکسان بدست می آورید. اما هر مثلث کاهش ناپذیر سه تایی فیثاغورثی دارای شکلی متفاوت از تمامی مثلث های کاهش ناپذیر دیگر می باشد.
مثلث \(8-15-17\) اولین مثلث سه تایی فیثاغورثی است که الگوی اشاره شده در بخش قبلی را دنبال نمی کند. در اینجا چگونگی تولید سه تایی هایی که الگوی \(8-15-17\) را دنبال می کنند، می بینید:
چند سه تایی بعدی از این مجموعۀ بی نهایت عبارتند از:
در ضمن، شما می توانید این فرآیند را در مورد سایر اعداد زوج استفاده کنید (اعدادی که مضربی از \(4\) نیستند) مانند \(10\) ، \(14\) ، \(18\) ، و به همین ترتیب. اما به مثلثی همچون \(10-24-26\) می رسید که دوبرابر شدۀ مثلث سه تایی فیثاغورثیِ \(5-12-13\) می باشد، و یک سه تایی کاهش ناپذیر با شکلی یکتا نمی باشد.
هر مثلث سه تایی کاهش ناپذیر مانند مثلث \(5-12-13\) مادر خانواده ای با تعداد بی نهایت فرزند می باشد. به عنوان مثال، خانوادۀ \(3:4:5\) ـــ به علامت کالن (:) توجه کنید ـــ عبارت از مثلث \(3-4-5\) و تمامی فرزندان آن می باشد. فرزندان این خاندان با بزرگ تر کردن یا کوچکتر کردن مثلث \(3-4-5\) ایجاد می شوند: آنها شامل مثلث \({3\over100}-{4\over100}-{5\over100}\) ، مثلث \(6-8-10\) ، مثلث \(21-28-35\) (\(3-4-5\) ضربدر \(7\))، و خواهر و برادرهای عجیب و غریب آنها همچون مثلث \(3\sqrt{11}-4\sqrt{11}-5\sqrt{11}\) و مثلث \(3 \pi-4\pi-5\pi\) و ... می باشند. تمامی اعضای خانوادۀ \(3:4:5\) ـــ یا هر خانوادۀ مثلثی دیگری ـــ دارای شکل مشابه با سایر مثلث های موجود در آن خانواده می باشد (آنها مشابه (similar) هستند ـــ در فصل 13 در مورد تشابه (similarity) جزئیات زیادی مطرح شده است).
هنگامی که شما فقط دو ضلع از سه ضلع یک مثلث قائم الزاویه را داشته باشید، می توانید ضلع سوم را با قضیۀ فیثاغورث محاسبه کنید. اما اگر آن مثلث بر حسب تصادف عضوی از خانوادۀ یکی از چهار مثلث سه تایی فیثاغورثیِ محبوب آغازین باشد ـــ و شما قادر باشید تا این واقعیت را متوجه شوید ـــ معمولاً می توانید در زمان و انرژیتان صرفه جویی کنید. تمام کاری که نیاز است تا انجام بدهید، اینست که فاکتور بزرگ شدن یا کوچک شدن که سه تایی محبوب را به مثلث داده شده تبدیل کرده است، بدست آورید و از آن فاکتور برای محاسبۀ ضلع نامشخص در آن مثلث استفاده کنید.
شما اغلب فقط یکی از خانوادۀ چهار سه تایی محبوب اول را می بینید و فاکتور بزرگ شدن یا کوچک شدن آن را به صورت ذهنی محاسبه می کنید. شکل 5-8 را بررسی کنید.
در بخش a از شکل 5-8 ، ارقام \(8\) و \(17\) در \(0.08\) و \(0.17\) باید به شما یک راهنمای قابل توجه بدهند که این مثلث عضوی از خانوادۀ \(8:15:17\) می باشد. زیرا \(8\) تقسیم بر \(100\) برابر است با \(0.08\) و \(17\) تقسیم بر \(100\) برابر است با \(0.17\) ، این مثلث یک مثلث \(8-15-17\) می باشد که \(100\) مرتبه کوچکتر شده است. بنابراین، ضلع \(j\) برابر است با \(15\) تقسیم بر \(100\)، یا \(0.15\) . خودشه. این میانبر قطعاً ساده تر از ، استفاده از قضیۀ فیثاغورث می باشد.
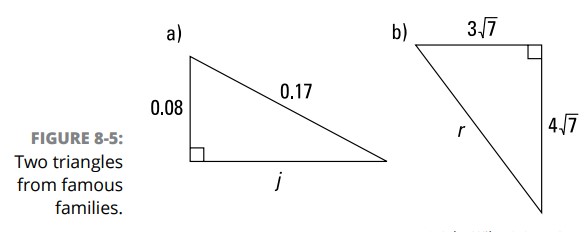
به همین ترتیب، ارقام \(3\) و \(4\) یک سرنخ آشکار از این می باشد که مثلث موجود در بخش b از شکل 5-8 عضوی از خانوادۀ \(3:4:5\) است. زیرا \(3\sqrt{7}\) برابر است با \(\sqrt{7}\) ضربدر \(3\) و \(4\sqrt{7}\) برابر است با \(\sqrt{7}\) ضربدر \(4\)، شما می توانید ببینید که این مثلث یک مثلث \(3-4-5\) می باشد که با فاکتوری از \(\sqrt{7}\) بزرگتر شده است. بنابراین، ضلع \(r\) به سادگی برابر با \(\sqrt{7}\) ضربدر \(5\) یا \(5\sqrt{7}\) می باشد.
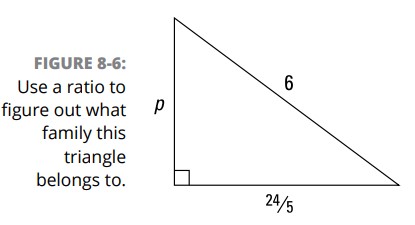
اگر نتوانید فوراً تشخیص دهید که یک مثلث به کدام خانوادۀ مثلث های سه تایی محبوب تعلق دارد، همواره می توانید از روش گام به گام زیر برای انتخاب خانواده و یافتن ضلع نامشخص استفاده کنید. به خاطر طولانی بودن این روش، آن را کنار نگذارید؛ انجام آن از توضیح دادنش ساده تر است. من از مثلث موجود در شکل 6-8 برای توصیف این فرآیند استفاده می کنم.
شما ممکن است با خودتان فکر کنید چرا شما باید وارد تمامی این مشکلات شوید، در صورتی که می توانید صرفاً از قضیۀ فیثاغورث استفاده کنید. نکته خوبی است. در مورد برخی از مثلث ها استفاده از قضیۀ فیثاغورث ساده تر است (مخصوصاً اگر اجازه داشته باشید از ماشین حسابتان استفاده کنید). اما ـــ به حرف من ایمان بیاورید ـــ این تکنیک مثلث سه تایی بسیار سودمند است. با این حال انتخاب با شماست.

یک مثلث چندتایی فیثاغورثی (Pythagorean triple triangle) یک مثلث قائم الزاویه می باشد که طول همۀ اضلاع آن اعداد کامل می باشند، مانند \(3\) ، \(4\) ، و \(5\)، یا \(5\) ، \(12\) ، و \(13\) . افراد تمایل دارند تا از این مثلث ها در مسائل استفاده کنند، زیرا شامل آن اعداد آزار دهندۀ زیر رادیکال نمی شوند. علیرغم اینکه بی نهایت از اینگونه مثلث ها وجود دارند، آنها بسیار نادر می باشند (مانند این واقعیت که مضربهای عدد \(100\) در بین سایر اعداد بسیار نادر هستند، حتی با وجود اینکه بی نهایت از این مضربها وجود دارند).
چهار مثلثِ محبوبِ سه تاییِ فیثاغورثی
چهار مثلث اول از نوع سه تایی فیثاغورثی محبوبِ طراحانِ مسائل هندسی می باشند. این سه تایی ها ـــ مخصوصاً مورد اول و دوم در این لیست که در ادامه آمده است ـــ در تمامی کتابهای هندسی ظاهر شده اند. (نکته: دو عدد اول در هر مثلث سه تایی طول ساق ها می باشند، و عدد سوم، یعنی بزرگترین عدد، طول وتر می باشد).
در اینجا چهار مثلث سه تایی فیثاغورثی اول را می بینید:
-
مثلث \(3-4-5\)
-
مثلث \(5-12-13\)
-
مثلث \(7-24-25\)
-
مثلث \(8-15-17\)
خوب است این چهار مثلث محبوب را به خاطر بسپارید، تا بتوانید آنها را به سرعت در آزمون ها تشخیص دهید.
ایجاد مثلث های سه تایی فیثاغورثیِ کاهش ناپذیر
به عنوان جایگزینی برای شمارش گوسفندان در هنگام خواب، ممکن است بخواهید بدانید چندتا مثلث سه تایی فیثاغورثیِ دیگر را می توانید بدست آورید.
سه تایِ اول در لیست پیشین یک الگو را دنبال می کنند. به عنوان مثال، مثلث \(5-12-13\) را در نظر بگیرید. مربع عدد کوچکتر، ساق فرد (\(5^2=25\)) مجموع ساق های بزرگتر و وتر می باشد (\(12+13=25\)). و ساق بزرگتر و وتر همیشه اعداد متوالی هستند. این الگو به شما امکان می دهد تا به هر تعداد مثلث که می خواهید تولید کنید. کاری که باید انجام بدهید در اینجا آمده است:
-
هر عدد فردی را بگیرید و آن را مربع سازید.
به عنوان مثال، \(9^2=81\)
-
دو عدد متوالی را بیابید که حاصل جمعشان این عدد می گردد.
\(40+41=81\)
شما اغلب به صورت ذهنی و بدون دقت و بررسی زیاد به این اعداد می رسید، اما اگر فوراً نتوانستید آنها را بیابید، کافیست \(1\) را از نتیجۀ مرحلۀ 1 تفریق کنید و سپس پاسخ آن را بر \(2\) تقسیم کنید:
$$\frac{81-1}{2}=40$$
نتیجۀ بدست آمده و عدد بزرگتر بعد از آن، دو عدد مد نظر شما می باشند.
-
عددی را که مربع کرده اید و دو عدد بدست آمده از مرحلۀ 2 را به صورت متوالی بنویسید تا تا مثلث خودتان را نامگذاری کنید.
شما یک مثلث سه تایی فیثاغورثی دیگر دارید: \(9-40-41\) .
در اینجا چند مثلث سه تایی فیثاغورثی بعدی، که این الگو را دنبال می کنند، می بینید:
-
\(11-60-61\) \((11^2=121;60+61=121)\)
-
\(13-84-85\) \((13^2=169;84+85=169)\)
-
\(15-112-113\) \((15^2=225;112+113=225)\)
این لیست بی پایان می باشد ـــ قادر است تا با بدترین نوع بیخوابی مقابله کند. و توجه داشته باشید که هر مثلث در این لیست کاهش ناپذیر (irreducible) می باشد؛ یعنی، مضربی از مثلث سه تایی فیثاغورثیِ کوچکتری نمی باشد (به عنوان مثال، در مقایسه با مثلث \(6-8-10\) ، که کاهش ناپذیر نمی باشد، زیرا دوبرابر شدۀ مثلث \(3-4-5\) است).
هنگامی که یک مثلث سه تایی فیثاغورثیِ جدید (مانند \(6-8-10\)) را با بزرگتر کردن یک مثلث سه تایی کوچکتر (\(3-4-5\)) می سازید، شما مثلث هایی با شکل دقیقاً یکسان بدست می آورید. اما هر مثلث کاهش ناپذیر سه تایی فیثاغورثی دارای شکلی متفاوت از تمامی مثلث های کاهش ناپذیر دیگر می باشد.
مثلث سه تایی فیثاغورثی با الگوی \(8-15-17\)
مثلث \(8-15-17\) اولین مثلث سه تایی فیثاغورثی است که الگوی اشاره شده در بخش قبلی را دنبال نمی کند. در اینجا چگونگی تولید سه تایی هایی که الگوی \(8-15-17\) را دنبال می کنند، می بینید:
-
هر مضربی از \(4\) را بگیرید.
فرض کنید انتخاب شما \(12\) باشد.
-
نصف آن را مربع سازید.
\((12 \div 2)^2 = 6^2=36\)
-
عدد مرحلۀ 1 و همینطور دو عدد فرد موجود در دو سمت نتیجۀ مرحلۀ 2 را بگیرید و با استفاده از آنها یک مثلث سه تایی فیثاغورثی بسازید.
\(12-35-37\)
چند سه تایی بعدی از این مجموعۀ بی نهایت عبارتند از:
-
\(16-63-65\) \((16 \div 2=8;8^2=64;63,65)\)
-
\(20-99-101\) \((20 \div 2 = 10;10^2=100;99,101)\)
-
\(24-143-145\) \((24 \div 2=12;12^2=144;143,145)\)
در ضمن، شما می توانید این فرآیند را در مورد سایر اعداد زوج استفاده کنید (اعدادی که مضربی از \(4\) نیستند) مانند \(10\) ، \(14\) ، \(18\) ، و به همین ترتیب. اما به مثلثی همچون \(10-24-26\) می رسید که دوبرابر شدۀ مثلث سه تایی فیثاغورثیِ \(5-12-13\) می باشد، و یک سه تایی کاهش ناپذیر با شکلی یکتا نمی باشد.
خانوادۀ مثلث های سه تایی فیثاغورثی
هر مثلث سه تایی کاهش ناپذیر مانند مثلث \(5-12-13\) مادر خانواده ای با تعداد بی نهایت فرزند می باشد. به عنوان مثال، خانوادۀ \(3:4:5\) ـــ به علامت کالن (:) توجه کنید ـــ عبارت از مثلث \(3-4-5\) و تمامی فرزندان آن می باشد. فرزندان این خاندان با بزرگ تر کردن یا کوچکتر کردن مثلث \(3-4-5\) ایجاد می شوند: آنها شامل مثلث \({3\over100}-{4\over100}-{5\over100}\) ، مثلث \(6-8-10\) ، مثلث \(21-28-35\) (\(3-4-5\) ضربدر \(7\))، و خواهر و برادرهای عجیب و غریب آنها همچون مثلث \(3\sqrt{11}-4\sqrt{11}-5\sqrt{11}\) و مثلث \(3 \pi-4\pi-5\pi\) و ... می باشند. تمامی اعضای خانوادۀ \(3:4:5\) ـــ یا هر خانوادۀ مثلثی دیگری ـــ دارای شکل مشابه با سایر مثلث های موجود در آن خانواده می باشد (آنها مشابه (similar) هستند ـــ در فصل 13 در مورد تشابه (similarity) جزئیات زیادی مطرح شده است).
هنگامی که شما فقط دو ضلع از سه ضلع یک مثلث قائم الزاویه را داشته باشید، می توانید ضلع سوم را با قضیۀ فیثاغورث محاسبه کنید. اما اگر آن مثلث بر حسب تصادف عضوی از خانوادۀ یکی از چهار مثلث سه تایی فیثاغورثیِ محبوب آغازین باشد ـــ و شما قادر باشید تا این واقعیت را متوجه شوید ـــ معمولاً می توانید در زمان و انرژیتان صرفه جویی کنید. تمام کاری که نیاز است تا انجام بدهید، اینست که فاکتور بزرگ شدن یا کوچک شدن که سه تایی محبوب را به مثلث داده شده تبدیل کرده است، بدست آورید و از آن فاکتور برای محاسبۀ ضلع نامشخص در آن مثلث استفاده کنید.
موارد خیلی آسان
شما اغلب فقط یکی از خانوادۀ چهار سه تایی محبوب اول را می بینید و فاکتور بزرگ شدن یا کوچک شدن آن را به صورت ذهنی محاسبه می کنید. شکل 5-8 را بررسی کنید.
در بخش a از شکل 5-8 ، ارقام \(8\) و \(17\) در \(0.08\) و \(0.17\) باید به شما یک راهنمای قابل توجه بدهند که این مثلث عضوی از خانوادۀ \(8:15:17\) می باشد. زیرا \(8\) تقسیم بر \(100\) برابر است با \(0.08\) و \(17\) تقسیم بر \(100\) برابر است با \(0.17\) ، این مثلث یک مثلث \(8-15-17\) می باشد که \(100\) مرتبه کوچکتر شده است. بنابراین، ضلع \(j\) برابر است با \(15\) تقسیم بر \(100\)، یا \(0.15\) . خودشه. این میانبر قطعاً ساده تر از ، استفاده از قضیۀ فیثاغورث می باشد.

به همین ترتیب، ارقام \(3\) و \(4\) یک سرنخ آشکار از این می باشد که مثلث موجود در بخش b از شکل 5-8 عضوی از خانوادۀ \(3:4:5\) است. زیرا \(3\sqrt{7}\) برابر است با \(\sqrt{7}\) ضربدر \(3\) و \(4\sqrt{7}\) برابر است با \(\sqrt{7}\) ضربدر \(4\)، شما می توانید ببینید که این مثلث یک مثلث \(3-4-5\) می باشد که با فاکتوری از \(\sqrt{7}\) بزرگتر شده است. بنابراین، ضلع \(r\) به سادگی برابر با \(\sqrt{7}\) ضربدر \(5\) یا \(5\sqrt{7}\) می باشد.
مطمئن شوید که اضلاع مثلث داده شده، به درستی با اضلاع خانوادۀ مثلث سه تایی محبوبی که از آن استفاده می کنید، مطابقت داشته باشد. به عنوان مثال، در یک مثلث \(3:4:5\) ، ساق ها باید \(3\) و \(4\) باشند، و وتر باید برابر با \(5\) باشد. بنابراین یک مثلث با ساق های \(30\) و \(50\) (علیرغم \(3\) و \(5\) در آن) عضوی از خانوادۀ \(3:4:5\) نمی باشد زیرا این \(50\) (یعنی \(5\)) یکی از ساق ها می باشد و نه وتر.
روش گام به گام تشخیص خانوادۀ یک مثلث سه تایی
اگر نتوانید فوراً تشخیص دهید که یک مثلث به کدام خانوادۀ مثلث های سه تایی محبوب تعلق دارد، همواره می توانید از روش گام به گام زیر برای انتخاب خانواده و یافتن ضلع نامشخص استفاده کنید. به خاطر طولانی بودن این روش، آن را کنار نگذارید؛ انجام آن از توضیح دادنش ساده تر است. من از مثلث موجود در شکل 6-8 برای توصیف این فرآیند استفاده می کنم.

-
دو ضلع معلوم را بگیرید و یک نسبت (ratio) برای ضلع کوچکتر به ضلع بزرگتر، بسازید (یا در شکل کسری و یا در شکل کالن).
\({24\over5}\) و \(6\) را بگیرید و نسبت زیر را بسازید:
$$\frac{{24\over5}}{6}$$
-
این نسبت را به پایین ترین عبارت آن با اعداد کامل، کاهش بدهید.
اگر صورت و مخرج \(\frac{{24\over5}}{6}\) را در \(5\) ضرب کنید، به \({24\over30}\) می رسید؛ این کسر به \({4\over5}\) کاهش می یابد. (با یک ماشین حساب، این مرحله به سادگی یک بشکن زدن می شود، زیرا بسیاری از ماشین حسابها دارای کارکردی می باشند که کسرها را به پایین ترین عبارت ممکنشان کاهش می دهند.)
-
به کسر مرحلۀ 2 نگاه کنید تا خانوادۀ مثلثی مخصوص آن را شناسایی نمایید.
اعداد \(4\) و \(5\) بخشی از مثلث \(3-4-5\) می باشند، بنابراین شما با خانوادۀ \(3:4:5\) درگیر هستید.
-
طول یک ضلع از مثلث داده شده را بر عدد متناظر آن از نسبت خانواده تقسیم کنید تا ضریبتان را بدست آورید (که به شما می گوید مثلث اصلی چقدر بزرگتر یا کوچکتر شده است).
از طول وتر در مثلث داده شده، استفاده کنید (زیرا کار کردن با یک عدد کامل، ساده تر است) و آن را بر \(5\) از نسبت \(3:4:5\) تقسیم کنید. شما باید به \({6\over5}\) به عنوان ضریب برسید.
-
عدد سوم خانواده (عددی که در کسر کاهش یافته شدۀ مرحلۀ 2 نمی بینید) را در نتایج مرحلۀ 4 ضرب کنید تا ضلع مجهول از مثلثتان را بدست آورید.
سه برابرِ \({6\over5}\) برابر است با \({18\over5}\) . این طول ضلع \(p\) می باشد؛ و کار تمام شده است.
شما ممکن است با خودتان فکر کنید چرا شما باید وارد تمامی این مشکلات شوید، در صورتی که می توانید صرفاً از قضیۀ فیثاغورث استفاده کنید. نکته خوبی است. در مورد برخی از مثلث ها استفاده از قضیۀ فیثاغورث ساده تر است (مخصوصاً اگر اجازه داشته باشید از ماشین حسابتان استفاده کنید). اما ـــ به حرف من ایمان بیاورید ـــ این تکنیک مثلث سه تایی بسیار سودمند است. با این حال انتخاب با شماست.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: