خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
استفاده از فرمولهای زاویه و قطر چندضلعی

در این بخش، فرمول هایی شامل زوایا و قطرها را مشاهده خواهید کرد. شما می توانید با استفاده از این فرمولها به برخی از سوالات پاسخ دهید که من شرط می بندم می توانستند شما را تا صبح بیدار نگهدارند:

تمام چیزهایی که در مورد یک چندضلعی باید بدانید الزاماً در اضلاع آنها قرار نگرفته اند. شما از زوایایی که بیرون یک چندضلعی قرار گرفته اند نیز استفاده خواهید کرد.
هنگام کار با چندضلعی ها از دو نوع از زوایا استفاده خواهید کرد (شکل 14-12 را ببینید):
شما می توانید فرمول های زوایای داخلی و خارجی را در مسألۀ سه بخشی زیر تمرین کنید: یک دوازه ضلعی منتظم (regular dodecagon) داریم:
به نظر می رسد معلوم نباشد این فرمول از کجا آمده است، آیا اینطور نیست؟ من قول می دهم که معنادار باشد، اما ابتدا باید اندکی درباره اش فکر کنید. (قطعاً که فقط حفظ کردنش کفایت می کند، اما در آنصورت دیگر جذابیتی نخواهد داشت؟)
در اینجا خاستگاه فرمول قطرها و دلیل درست کار کردن آن را داریم. هر قطر یک نقطه را به نقطه ای دیگر در یک چندضلعی متصل می کند که همسایۀ بغلی اش نباشد. در یک \(n\)ضلعی، شما \(n\) نقطۀ آغاز برای قطرها دارید. و هر قطر می تواند به (\(n-3\)) نقطۀ پایانی برود، زیرا یک قطر نمی تواند به نقطۀ آغازین خودش یا هر کدام از دو نقطۀ کناری اش متصل گردد. بنابراین اولین مرحله اینست که آن را در (\(n-3\)) ضرب کنیم. سپس، از آنجا که نقطۀ پایانی هر قطر، خودش می تواند به عنوان نقطۀ آغازین نیز باشد، حاصلضرب \(n(n-3)\) هر قطر را دوبار شمارش می کند. دلیل اینکه حاصل را بر \(2\) تقسیم می کنید این می باشد.
در اینجا یک مسألۀ دیگر را برای شما داریم: اگر یک چندضلعی دارای \(90\) قطر باشد، دارای چند ضلع می باشد؟
شما فرمول تعداد قطرهای یک چندضلعی را می دانید، و همینطور می دانید که این چندضلعی دارای \(90\) قطر می باشد، بنابراین \(90\) را در پاسخ جایگذاری کنید و معادلۀ بدست آمده را برای یافتن \(n\) حل کنید:
$$
\frac{n(n-3)}{2}=90 \\
n^2-3n=180 \\
n^2-3n-180=0\\
(n-15)(n+12)=0
$$
بنابراین، \(n\) برابر با \(15\) یا \(-12\) می باشد. اما از آنجا که یک چندضلعی نمی تواند دارای تعداد اضلاع منفی باشد، بنابراین \(n\) باید \(15\) باشد. پس شما یک چندضلعی با \(15\) ضلع (pentadecagon) دارید.

-
یک چندضلعی با \(100\) ضلع چند قطر دارد؟ پاسخ: \(4,850\)
-
مجموع تمامی زوایای یک بیست ضلعی چقدر می باشد؟ پاسخ: \(3,240^{\circ}\)
زوایای داخلی و زوایای خارجی در چندضلعی ها
تمام چیزهایی که در مورد یک چندضلعی باید بدانید الزاماً در اضلاع آنها قرار نگرفته اند. شما از زوایایی که بیرون یک چندضلعی قرار گرفته اند نیز استفاده خواهید کرد.
هنگام کار با چندضلعی ها از دو نوع از زوایا استفاده خواهید کرد (شکل 14-12 را ببینید):
-
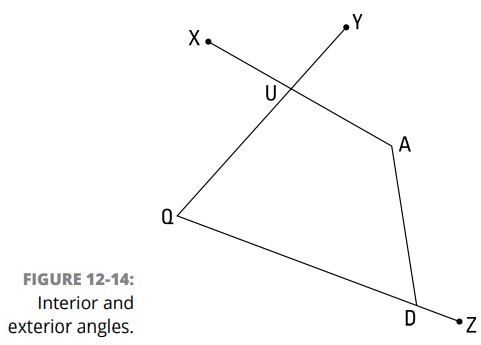
زاویه داخلی (Interior angle): یک زاویۀ داخلی از یک چندضلعی، زاویه ای است که درون آن چندضلعی و در یکی از رأس های آن قرار گرفته است. زاویۀ \(Q\) یک زاویۀ داخلی از چهار ضلعیِ \(QUAD\) می باشد.
-
زاویۀ خارجی (Exterior angle): یک زاویۀ خارجی از یک چندضلعی، زاویه ای است که بیرون آن چندضلعی قرار دارد و توسط یکی از اضلاع آن و امتداد یک ضلع مجاور آن شکل گرفته است. زاویۀ \(ADZ\) ، \(\angle{XUQ}\) ، و \(\angle{YUA}\) زوایایی خارجی در \(QUAD\) می باشند؛ زاویۀ متقابل به رأس \(XUY\) یک زاویۀ خارجی از \(QUAD\) نمی باشد.

فرمول های زوایای داخلی و خارجی:
-
مجموع اندازۀ زوایای داخلی یک چندضلعی که دارای \(n\) ضلع می باشد برابر است با:
$$(n-2)180$$
-
اندازۀ هر زاویۀ داخلی در یک \(n\)ضلعیِ متساوی الزوایا برابر است با:
$$\frac{(n-2)180}{n}$$
یا برابر است با مکمل یک زاویۀ خارجی:
$$180-\frac{360}{n}$$
-
اگر یک زاویۀ خارجی را در هر رأس یک چندضلعی شمارش کنید، مجموع این زوایای خارجی از چندضلعی برابر با \(360^{\circ}\) خواهد بود.
-
اندازۀ هر زاویۀ خارجی در یک \(n\)ضلعیِ متساوی الزاویا برابر است با:
$$\frac{360}{n}$$
مسأله ای از زوایای داخلی و خارجی یک چندضلعی
شما می توانید فرمول های زوایای داخلی و خارجی را در مسألۀ سه بخشی زیر تمرین کنید: یک دوازه ضلعی منتظم (regular dodecagon) داریم:
-
مجموع زوایای داخلی آن را بیابید.
کافیست تعداد اضلاع (\(12\)) در فرمول مجموع زوایای داخلی یک چندضلعی جایگذاری کنید:
$$(n-2)180 = (12-2)180=1,800^{\circ}$$
-
اندازۀ یک زاویۀ داخلی را بیابید.
این چندضلعی \(12\) ضلع دارد، بنابراین دارای \(12\) زاویه می باشد؛ و از آنجا که شما با یک چندضلعی منتظم سر و کار دارید، تمامی اضلاع آن همنهشت می باشند. بنابراین، برای یافتن اندازۀ یک زاویۀ واحد، کافیست پاسخ بدست آمده در بخش یک از این مسأله را بر \(12\) تقسیم کنید. (توجه داشته باشید که این اساساً با فرمول اول یافتن اندازۀ یک زاویۀ واحد یکسان می باشد.)
$$\frac{1,800}{12}=150^{\circ}$$
-
اندازۀ یک زاویۀ واحد خارجی را با استفاده از فرمول زاویۀ خارجی بیابید؛ سپس مکمل آن را بررسی کنید، مکمل آن باید با یک زاویۀ داخلی که در بخش 2 از این مسأله بدست آوردید یکسان باشد.
ابتدا \(12\) را در فرمول بسیار سادۀ زاویۀ خارجی جایگذاری کنید:
$$\frac{360}{12}=30^{\circ}$$
اکنون مکمل این پاسخ را بدست آورید تا اندازۀ یک زاویۀ واحد داخلی را داشته باشید، و بررسی کنید که این پاسخ با پاسخ بدست آمده در بخش 2 از این مسأله یکسان باشد:
$$180-30=150^{\circ}$$
پاسخ صحیح است. (و توجه داشته باشید که آخرین محاسبه اساساً با استفاده از فرمول دوم برای یک زاویۀ واحد داخلی، چیز یکسانی می باشند.)
قطرها در چندضلعی
تعداد قطرها در یک \(n\)ضلعی: تعداد قطرهایی که می توانید در یک \(n\)ضلعی ترسیم کنید برابر است با:
$$\frac{n(n-3)}{2}$$
$$\frac{n(n-3)}{2}$$
به نظر می رسد معلوم نباشد این فرمول از کجا آمده است، آیا اینطور نیست؟ من قول می دهم که معنادار باشد، اما ابتدا باید اندکی درباره اش فکر کنید. (قطعاً که فقط حفظ کردنش کفایت می کند، اما در آنصورت دیگر جذابیتی نخواهد داشت؟)
در اینجا خاستگاه فرمول قطرها و دلیل درست کار کردن آن را داریم. هر قطر یک نقطه را به نقطه ای دیگر در یک چندضلعی متصل می کند که همسایۀ بغلی اش نباشد. در یک \(n\)ضلعی، شما \(n\) نقطۀ آغاز برای قطرها دارید. و هر قطر می تواند به (\(n-3\)) نقطۀ پایانی برود، زیرا یک قطر نمی تواند به نقطۀ آغازین خودش یا هر کدام از دو نقطۀ کناری اش متصل گردد. بنابراین اولین مرحله اینست که آن را در (\(n-3\)) ضرب کنیم. سپس، از آنجا که نقطۀ پایانی هر قطر، خودش می تواند به عنوان نقطۀ آغازین نیز باشد، حاصلضرب \(n(n-3)\) هر قطر را دوبار شمارش می کند. دلیل اینکه حاصل را بر \(2\) تقسیم می کنید این می باشد.
در اینجا یک مسألۀ دیگر را برای شما داریم: اگر یک چندضلعی دارای \(90\) قطر باشد، دارای چند ضلع می باشد؟
شما فرمول تعداد قطرهای یک چندضلعی را می دانید، و همینطور می دانید که این چندضلعی دارای \(90\) قطر می باشد، بنابراین \(90\) را در پاسخ جایگذاری کنید و معادلۀ بدست آمده را برای یافتن \(n\) حل کنید:
$$
\frac{n(n-3)}{2}=90 \\
n^2-3n=180 \\
n^2-3n-180=0\\
(n-15)(n+12)=0
$$
بنابراین، \(n\) برابر با \(15\) یا \(-12\) می باشد. اما از آنجا که یک چندضلعی نمی تواند دارای تعداد اضلاع منفی باشد، بنابراین \(n\) باید \(15\) باشد. پس شما یک چندضلعی با \(15\) ضلع (pentadecagon) دارید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: