خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
رابطه های طولی در دایره

مانند بخش های پیشین، در این بخش هم آنچه را که هنگام تقاطع بین زوایا و دایره ها اتفاق می افتد بررسی می کنیم. اما این بار، به جای تجزیه و تحلیل اندازۀ زوایا و کمان ها، شما طول پاره خطهایی را که آن زوایا را می سازند، مورد تجزیه و تحلیل قرار می دهید. برای این کار سه قضیه وجود دارد که با نام قضایای پاوِر (Power Theorems) شناخته می شوند. سه قضیۀ پاور که در ادامه آمده است شما را قادر می سازند تا تمامی انواع مسأله های جذاب دایره را حل کنید.

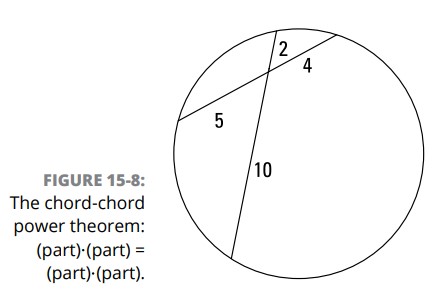
به عنوان مثال، در شکل 8-15 :
$$5 \cdot 4 = 10 \cdot 2$$
مهارتهای قضیه پاور خود را روی این مسأله امتحان کنید:
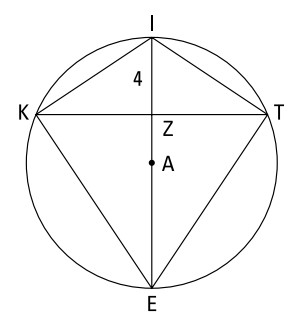
داده ها:
دایرۀ \(A\) دارای شعاع \(6.5\) می باشد
\(KITE\) یک کایت است
\(IZ=4\)
پیدا کنید:
مساحت \(KITE\)
برای بدست آوردن مساحت یک کایت، نیاز دارید تا طول قطرهای آن را بدانید. قطرهای این کایت دو وتر می باشند که از یکدیگر عبور کرده اند، بنابراین باید از خودتان بپرسید، آیا می توانید قضیۀ پاور وتر-وتر را به کار ببرید.
برای بدست آوردن قطر \(\overline{IE}\) ، توجه داشته باشید که \(\overline{IE}\) قطری از این دایره نیز می باشد. دایرۀ \(A\) دارای شعاع \(6.5\) است، بنابراین قطر آن دو برابر طول شعاع، یا \(13\) می باشد، و از اینرو این طول قطر \(\overline{IE}\) نیز می باشد. سپس می بینید که \(ZE\) باید برابر با \(13-9\)، یا \(9\) باشد. اکنون دو تا از طول های مربوط به پاره خطهایی که در این قضیه استفاده خواهید کرد را دارید، \(IZ=4\) و \(ZE=9\) .
$$(KZ)(ZT)=(IZ)(ZE)$$
از آنجا که \(KITE\) یک کایت می باشد، قطر \(\overline{IE}\) قطر \(\overline{KT}\) را تنصیف می کند (برای مشاهده ویژگیهای کایت فصل 10 را ببینید.) از این رو، \(\overline{KZ} \cong \overline{ZT}\) ، بنابراین می توانید هر دوی آنها را برابر با \(x\) قرار دهید. همه چیز را در معادله جایگذاری کنید:
$$
x \cdot x=4 \cdot 9 \\
x^2=36 \\
x=6 \text{ or } x=-6
$$
بدیهی است که می توانید مقدار \(-6\) را به عنوان طول یک پاره خط، نادیده بگیرید، بنابراین \(x\) برابر با \(6\) می باشد. \(KZ\) و \(ZT\) هر دو برابر با \(6\) می باشند، و از اینرو قطر \(\overline{KT}\) برابر با \(12\) خواهد بود. شما هم اکنون طول قطر دیگر را نیز بدست آورده اید، بنابراین می توانید با فرمول مساحت کایت این مسأله را تمام کنید:
$$
\text{Area}_{KITE}=\frac{1}{2}d_1d_2 \\
=\frac{1}{2} \cdot 12 \cdot 13 \\
= 78 \text{ units}^2
$$
ضمناً، شما می توانید این مسأله را با قضیۀ ارتفاع وارد بر وتر (altitude-on-hypotenuse theorem)، که در فصل 13 به شما معرفی کردم، انجام دهید. زوایای \(IKE\) و \(ITE\) نیم دایره های \(180^{\circ}\) را قطع کرده اند، بنابراین هر دوی آنها نصفِ \(180^{\circ}\) ، یا زوایای قائمه می باشند. قضیۀ ارتفاع وارد بر وتر به شما این روابط را برای این دو مثلث قائم الزاویه در سمت راست و چپ کایت می دهد:
$$
(KZ)^2=(IZ)(ZE) \\
(TZ)^2=(IZ)(ZE)
$$
بعد از آن، از لحاظ ریاضی درست مانند اینست که از قضیۀ پاور وتر-وتر استفاده کرده باشید.
در این بخش، وارد مبحث قضیۀ پاور تانژانت-سکانت می شوم.
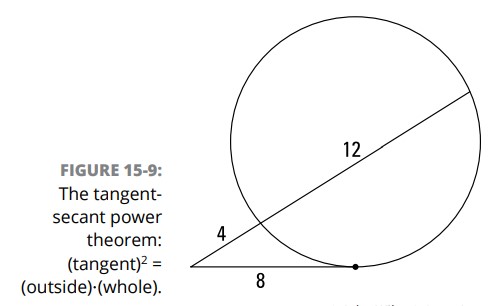
به عنوان مثال، در شکل 9-15 :
$$8^2=4(4+12)$$
آخرین و اما نه کم اهمیت ترین، قضیه ای که به شما خواهم گفت، قضیۀ پاور سکانت-سکانت می باشد.
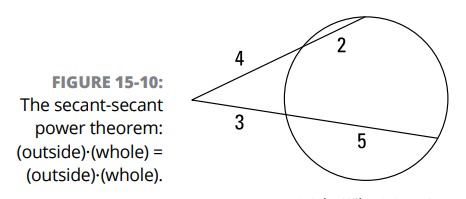
به عنوان مثال، در شکل 10-15 :
$$4(4+2)=3(3+5)$$
مسالۀ زیر از این دو قضیۀ پاور آخر استفاده می کند:
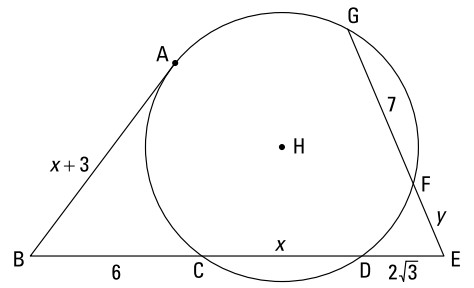
داده ها:
شکل هندسی به نحویکه می بینید
\(\overline{BA}\) یک تانژانت به دایرۀ \(H\) در نقطۀ \(A\) می باشد
پیدا کنید:
\(x\) و \(y\)
این شکل شامل یک تانژانت و چند سکانت می باشد، بنابراین به قضایای پاور تانژانت-سکانت و سکانت-سکانت نگاهی بیندازید. ابتدا از قضیۀ پاور تانژانت-سکانت با تانژانت \(\overline{AB}\) و سکانت \(\overline{BD}\) استفاده کنید تا \(x\) را بدست آورید:
$$
(x+3)^2=6(6+x) \\
x^2+6x+9=36+6x \\
x^2=27 \\
x=\pm \sqrt{27} \\
x=\pm 3\sqrt{3}
$$
شما می توانید این پاسخ منفی را نادیده بگیرید، پس \(x\) برابر با \(3\sqrt{3}\) می باشد.
اکنون از قضیۀ پاور سکانت-سکانت با سکانت های \(\overline{EC}\) و \(\overline{EG}\) استفاده کنید تا \(y\) را بدست آورید:
$$
(2\sqrt{3})(2\sqrt{3}+3\sqrt{3})=y(y+7) \\
2\sqrt{3} \cdot 5\sqrt{3} = y^2+7y \\
30=y^2+7y \\
y^2+7y-30=0 \\
(y+10)(y-3)=0 \\
y+10=0 \text{ or } y-3=0 \\
y=-10 \text{ or } y=3
$$
یک پاره خط نمی تواند طول منفی داشته باشد، پس \(y=3\) . تمام شد.
این طرح کلی یکی شده می تواند به شما کمک کند هر سۀ این قضایا را که در این بخش مطرح کردم به خاطر بسپارید. و می تواند به شما کمک کند تا از اشتباه رایجِ ضرب کردن بخش بیرونیِ یک سکانت در بخش درونی آن (به جای ضرب کردن بخش بیرونی در کل سکانت) در هنگام استفاده از قضیۀ تانژانت-سکانت یا قضیۀ پاور سکانت-تانژانت، اجتناب کنید.

قضیۀ پاور وتر-وتر
قضیۀ پاور وتر-وتر (chord-chord power theorem): اگر دو وتر از یک دایره همدیگر را قطع کنند، آن گاه حاصلضرب طول دو بخش از یک وتر برابر است با حاصلضرب طول دو بخش از وتر دیگر.
به عنوان مثال، در شکل 8-15 :
$$5 \cdot 4 = 10 \cdot 2$$

مهارتهای قضیه پاور خود را روی این مسأله امتحان کنید:

داده ها:
دایرۀ \(A\) دارای شعاع \(6.5\) می باشد
\(KITE\) یک کایت است
\(IZ=4\)
پیدا کنید:
مساحت \(KITE\)
برای بدست آوردن مساحت یک کایت، نیاز دارید تا طول قطرهای آن را بدانید. قطرهای این کایت دو وتر می باشند که از یکدیگر عبور کرده اند، بنابراین باید از خودتان بپرسید، آیا می توانید قضیۀ پاور وتر-وتر را به کار ببرید.
برای بدست آوردن قطر \(\overline{IE}\) ، توجه داشته باشید که \(\overline{IE}\) قطری از این دایره نیز می باشد. دایرۀ \(A\) دارای شعاع \(6.5\) است، بنابراین قطر آن دو برابر طول شعاع، یا \(13\) می باشد، و از اینرو این طول قطر \(\overline{IE}\) نیز می باشد. سپس می بینید که \(ZE\) باید برابر با \(13-9\)، یا \(9\) باشد. اکنون دو تا از طول های مربوط به پاره خطهایی که در این قضیه استفاده خواهید کرد را دارید، \(IZ=4\) و \(ZE=9\) .
$$(KZ)(ZT)=(IZ)(ZE)$$
از آنجا که \(KITE\) یک کایت می باشد، قطر \(\overline{IE}\) قطر \(\overline{KT}\) را تنصیف می کند (برای مشاهده ویژگیهای کایت فصل 10 را ببینید.) از این رو، \(\overline{KZ} \cong \overline{ZT}\) ، بنابراین می توانید هر دوی آنها را برابر با \(x\) قرار دهید. همه چیز را در معادله جایگذاری کنید:
$$
x \cdot x=4 \cdot 9 \\
x^2=36 \\
x=6 \text{ or } x=-6
$$
بدیهی است که می توانید مقدار \(-6\) را به عنوان طول یک پاره خط، نادیده بگیرید، بنابراین \(x\) برابر با \(6\) می باشد. \(KZ\) و \(ZT\) هر دو برابر با \(6\) می باشند، و از اینرو قطر \(\overline{KT}\) برابر با \(12\) خواهد بود. شما هم اکنون طول قطر دیگر را نیز بدست آورده اید، بنابراین می توانید با فرمول مساحت کایت این مسأله را تمام کنید:
$$
\text{Area}_{KITE}=\frac{1}{2}d_1d_2 \\
=\frac{1}{2} \cdot 12 \cdot 13 \\
= 78 \text{ units}^2
$$
ضمناً، شما می توانید این مسأله را با قضیۀ ارتفاع وارد بر وتر (altitude-on-hypotenuse theorem)، که در فصل 13 به شما معرفی کردم، انجام دهید. زوایای \(IKE\) و \(ITE\) نیم دایره های \(180^{\circ}\) را قطع کرده اند، بنابراین هر دوی آنها نصفِ \(180^{\circ}\) ، یا زوایای قائمه می باشند. قضیۀ ارتفاع وارد بر وتر به شما این روابط را برای این دو مثلث قائم الزاویه در سمت راست و چپ کایت می دهد:
$$
(KZ)^2=(IZ)(ZE) \\
(TZ)^2=(IZ)(ZE)
$$
بعد از آن، از لحاظ ریاضی درست مانند اینست که از قضیۀ پاور وتر-وتر استفاده کرده باشید.
قضیۀ پاور تانژانت-سکانت
در این بخش، وارد مبحث قضیۀ پاور تانژانت-سکانت می شوم.
قضیۀ پاور تانژانت-سکانت (tangent-secant power theorem): اگر یک تانژانت و یک سکانت از یک نقطۀ بیرونی به یک دایره ترسیم شوند، آن گاه مربع طول آن تانژانت برابر است با حاصلضرب طول بخش بیرونی آن سکانت در طول کل آن سکانت.
به عنوان مثال، در شکل 9-15 :
$$8^2=4(4+12)$$

قضیۀ پاور سکانت-سکانت
آخرین و اما نه کم اهمیت ترین، قضیه ای که به شما خواهم گفت، قضیۀ پاور سکانت-سکانت می باشد.
قضیۀ پاور سکانت-سکانت (Secant-Secant Power Theorem): اگر دو سکانت از یک نقطۀ بیرونی به یک دایره ترسیم شوند، آن گاه حاصلضرب طول بخش بیرونیِ یک سکانت در طول کل آن سکانت برابر است با حاصلضرب طول بخش بیرونی سکانت دیگر در طول کل آن سکانت دیگر.
به عنوان مثال، در شکل 10-15 :
$$4(4+2)=3(3+5)$$

مسالۀ زیر از این دو قضیۀ پاور آخر استفاده می کند:

داده ها:
شکل هندسی به نحویکه می بینید
\(\overline{BA}\) یک تانژانت به دایرۀ \(H\) در نقطۀ \(A\) می باشد
پیدا کنید:
\(x\) و \(y\)
این شکل شامل یک تانژانت و چند سکانت می باشد، بنابراین به قضایای پاور تانژانت-سکانت و سکانت-سکانت نگاهی بیندازید. ابتدا از قضیۀ پاور تانژانت-سکانت با تانژانت \(\overline{AB}\) و سکانت \(\overline{BD}\) استفاده کنید تا \(x\) را بدست آورید:
$$
(x+3)^2=6(6+x) \\
x^2+6x+9=36+6x \\
x^2=27 \\
x=\pm \sqrt{27} \\
x=\pm 3\sqrt{3}
$$
شما می توانید این پاسخ منفی را نادیده بگیرید، پس \(x\) برابر با \(3\sqrt{3}\) می باشد.
اکنون از قضیۀ پاور سکانت-سکانت با سکانت های \(\overline{EC}\) و \(\overline{EG}\) استفاده کنید تا \(y\) را بدست آورید:
$$
(2\sqrt{3})(2\sqrt{3}+3\sqrt{3})=y(y+7) \\
2\sqrt{3} \cdot 5\sqrt{3} = y^2+7y \\
30=y^2+7y \\
y^2+7y-30=0 \\
(y+10)(y-3)=0 \\
y+10=0 \text{ or } y-3=0 \\
y=-10 \text{ or } y=3
$$
یک پاره خط نمی تواند طول منفی داشته باشد، پس \(y=3\) . تمام شد.
فشرده کردن قضایای پاوردر یک مفهوم واحد
هر سه قضیۀ پاور شامل یک معادله با حاصلضرب دو طول (یا یک طول مربع شده) می باشند که با حاصلضرب دیگری از طول ها برابر می باشند. و هر طول یک فاصله از رأس یک زاویه تا لبۀ آن دایره می باشد. از اینرو، هر سۀ این قضایا دارای طرح کلی یکسانی می باشند:
$$(\text{vertex to circle}) \cdot (\text{vertex to circle}) = (\text{vertex to circle}) \cdot (\text{vertex to circle})$$
$$(\text{vertex to circle}) \cdot (\text{vertex to circle}) = (\text{vertex to circle}) \cdot (\text{vertex to circle})$$
ترجمۀ فرمول:
vertex to circle: رأس تا دایره
vertex to circle: رأس تا دایره
این طرح کلی یکی شده می تواند به شما کمک کند هر سۀ این قضایا را که در این بخش مطرح کردم به خاطر بسپارید. و می تواند به شما کمک کند تا از اشتباه رایجِ ضرب کردن بخش بیرونیِ یک سکانت در بخش درونی آن (به جای ضرب کردن بخش بیرونی در کل سکانت) در هنگام استفاده از قضیۀ تانژانت-سکانت یا قضیۀ پاور سکانت-تانژانت، اجتناب کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: