چیزی که من به آنها شکل های نوک تیز می گویم، شکل های سه بعدی با یک قاعدۀ مسطح و یک نوک تیز می باشند. شکل های سه بعدی نوک تیز شامل هرم و مخروط می باشند. علیرغم اینکه هرم یک قاعده در شکل چندضلعی و مخروط یک قاعدۀ مدور دارد، فرمول های حجم و مساحت رویۀ آنها بسیار شبیه یکدیگر می باشند و به لحاظ مفهومی یکسان هستند. در ادامه جزئیات بیشتری در مورد هرم ها و مخروط ها آمده است:

• هرم (Pyramid): هرم یک شکل سه بعدی با یک قاعدۀ چندضلعی و کناره هایی می باشد که از قاعده امتداد یافته اند تا همدیگر را در یک نقطه ملاقات کنند. همانند منشور، گوشه های هرم رأس ها (vertices) نامیده می شوند، و پاره خطهایی که این رأس ها را به یکدیگر متصل می کنند یال ها (edges) نامیده می شوند، و کناره های مسطح وجه ها (faces) نامیده می شوند.
  
  یک هرم منتظم (regular pyramid) هرمی است که قاعدۀ آن یک چندضلعی منتظم باشد، که قلۀ هرم مستقیماً بالای مرکز قاعدۀ آن باشد. وجه های جانبیِ یک هرم منتظم همگی همنهشت می باشند. تمامی هرم ها در این کتاب، و اغلب هرم ها در سایر کتاب های هندسی، هرم های منتظم می باشند. هرگاه که من واژۀ هرم را به کار می برم، منظورم یک هرم منتظم می باشد.
  
  
• مخروط (Cone): مخروط یک شکل سه بعدی با یک قاعدۀ مدور و رویۀ جانبی مدور می باشد که قاعده را به یک نقطۀ مشترک متصل می کنند.
  
  یک مخروط قائم دوار (right circular cone) مخروطی با یک قاعدۀ مدور می باشد که قلۀ آن مستقیماً بالای مرکز قاعدۀ آن قرار دارد. تمامی مخروط های این کتاب، و اغلب مخروط ها در سایر کتابهای هندسی، مخروط های قائم دوار می باشند. هنگامی که من به یک مخروط اشاره می کنم، منظورم مخروط قائم دوار می باشد.
  

اکنون که درک بهتری از این شکلها دارید، فرمولهای حجم و مساحت رویۀ آنها را بررسی کنید:



مساحت رویۀ جانبی (lateral area) در یک شکل نوک تیز (هرم و مخروط) مساحتی از رویه می باشد که قاعده را به قله (رأس) متصل می کند (مساحت همه چیز به جز مساحت قاعده می باشد). در اینجا معنای آن را برای هرم ها و مخروط ها می بینید:

• مساحت جانبی در یک هرم از مثلث ها تشکیل شده است.
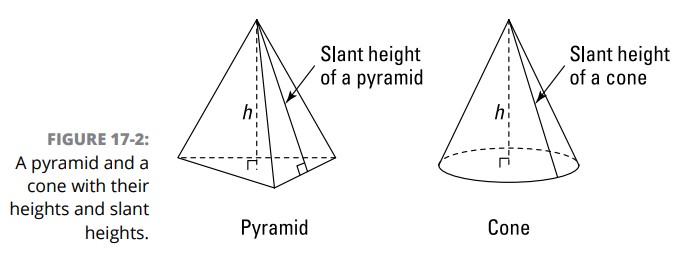
  هر وجه جانبی در یک هرم یک مثلث می باشد که مساحت آن با فرمول مساحت معمولی مثلث بدست می آید، \(\text{Area}=\frac{1}{2}(\text{base})(\text{height})\) . اما شما نمی توانید از ارتفاع هرم به عنوان ارتفاع وجه مثلثی شکل آن استفاده کنید ـــ این ارتفاع در امتداد وجه مثلثی شکل پایین نمی رود. بنابراین به جای آن، از سهم هرم (pyramid’s slant height) استفاده می کنید، که صرفاً همان ارتفاع معمولی آن وجه مثلثی شکل می باشد. (حرف شکستۀ \(\ell\) سهم هرم را نشان می دهد.) شکل 2-17 تفاوت بین ارتفاع و سهم هرم را نشان می دهد.
  
  
• مساحت جانبی یک مخروط در اصل یک مثلث است که به شکل یک مخروط پیچیده شده است.
  مساحت جانبی یک مخروط یک مثلث است که مانند یک ظرف بستنیِ مخروطی به شکل یک مخروط پیچیده شده است (آن فقط نوعی از یک مثلث است، زیرا هنگامی که مسطح شود، در واقع یک قطاع از یک دایره با یک ضلع پایینی منحنی شکل می باشد ـــ برای اطلاعات بیشتر در مورد قطاع ها، فصل 15 را ببینید.) مساحت آن برابر با \(\frac{1}{2}(\text{base})(\text{slant height})\) می باشد، درست مانند مساحت یکی از مثلث های جانبی در یک هرم. قاعدۀ این مثلث برابر با محیط قاعدۀ مخروط می باشد (این مسأله درست مانند مستطیل جانبی در یک استوانه عمل می کند).
  

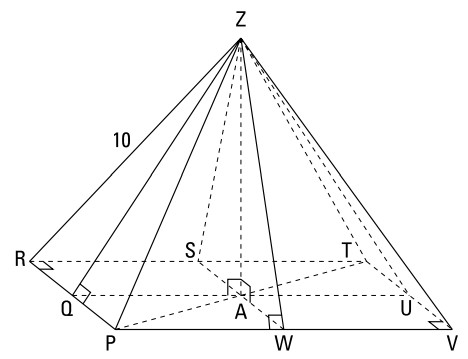
برای یک مسالۀ هرم آماده اید؟

داده ها:
یک هرم منتظم
قطر \(\overline{PT}\) دارای طول \(12\) می باشد
طول \(\overline{RZ}\) برابر با \(10\) می باشد
پیدا کنید:

1. حجم این هرم
   
2. مساحت رویۀ این هرم
   

مثلث های قائم الزوایۀ همنهشت در همه جای هرم ها هستند. آیا باور می کنید که در هرمی مشابه هرم موجود در این مسأله، \(28\) مثلث قائم الزاویۀ متفاوت وجود دارند که می توانید از آنها برای حل کردن بخشهای مختلف این مسأله استفاده کنید؟ (بسیاری از این مثلث ها در این شکل نشان داده نشده اند.) آنها به این شرح می باشند:

• هشت مثلث قائم الزاویۀ همنهشت، مانند \(\triangle{PZW}\)، در وجه ها می باشند (زوایای قائمۀ آنها در \(W\)، \(Q\) ، \(S\) ، یا \(U\) می باشند).
  
  
• هشت مثلث قائم الزوایه سرپا ایستاده اند و زوایای قائمۀ آنها در \(A\) و یک رأس آنها در \(Z\) قرار دارند. چهار تا از این مثلث ها یک رأسشان در \(Q\)، \(S\)، \(U\)، یا \(V\) می باشند (مانند \(\triangle{QZA}\)) که با یکدیگر همنهشت می باشند، و چهارتای دیگر دارای یک رأس در \(P\)، \(R\)، \(T\)، یا \(V\) می باشند که با یکدیگر همنهشتند (مانند \(\triangle{PZA}\)).
  
  
• شما چهار نصفۀ مربع مانند \(\triangle{PTV}\) دارید. این مثلث ها همنهشت و \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشند.
  
  
• درون قاعده، هشت مثلث قائم الزاویۀ کوچک همنهشت و \(45^{\circ}-45^{\circ}-90^{\circ}\) مانند \(\triangle{PAW}\) وجود دارند.
  

(در صورتیکه کنجکاو باشید، در آنجا \(48\) مثلث قائم الزوایۀ دیگر هم داریم ـــ بسته به اینکه چگونه آنها را شمارش کنید ـــ که احتمال اینکه از آنها استفاده کنید بسیار بعید است، که مجموع این مثلث های قائم الزاویه را به \(76\) می رساند!)

اوکی، به این مسالۀ هرم بازگردیم.

1. حجم این هرم را بیابید.
   برای محاسبۀ حجم یک هرم، به ارتفاع آن (\(\overline{AZ}\)) و مساحت قاعدۀ آن (\(PRTV\)) نیاز دارید. شما می توانید با حل کردن مثلث قائم الزاویۀ \(\triangle{PZA}\) ارتفاع را بدست آورید. یال های جانبی در یک هرم منتظم همنهشت می باشند؛ از اینرو، وتر \(\triangle{PZA}\) ، یعنی \(\overline{PZ}\) ، با \(\overline{RZ}\) همنهشت می باشد، بنابراین طول آن نیز برابر با \(10\) می باشد. \(\overline{PA}\) نصف قطر قاعده می باشد، بنابراین برابر با \(6\) است. بنابراین، مثلث \(PZA\) یک مثلث \(3-4-5\) است که اندازه اش دوبرابر شده است، یعنی یک مثلث \(6-8-10\) شده است، پس ارتفاع، \(\overline{AZ}\) ، برابر با \(8\) است (یا شما می توانید از قضیۀ فیثاغورث برای بدست آوردن \(\overline{AZ}\) استفاده کنید ـــ برای اطلاعات بیشتر در مورد هر دوی این روش ها فصل 8 را ببینید).
   
   برای بدست آوردن مساحت مربع \(PRTV\) ، شما می توانید ابتدا طول اضلاع آن را بدست آورید؛ اما فراموش نکنید که یک مربع یک کایت نیز می باشد، پس می توانید از فرمول مساحت کایت نیز استفاده کنید ـــ اگر قطر یک مربع را بدانید این روش سریعترین روش برای محاسبۀ مساحتش می باشد (برای اطلاعات بیشتر در مورد چهارضلعی ها فصل 10 را ببینید). از آنجا که قطرهای یک مربع برابر می باشند، هر دوی آنها برابر با \(12\) هستند، و شما تمام چیزهای لازم برای استفاده از فرمول مساحت کایت را دارید:
   $$
   \text{Area}_{PRTV}=\frac{1}{2}d_1d_2 \\
   =\frac{1}{2}(12)(12) \\
   =72 \text{ units}^2
   $$
   اکنون از فرمول حجم هرم استفاده کنید:
   $$
   \text{Vol}_{\text{Pyramid}}=\frac{1}{3} \text{area}_{\text{base}} \cdot \text{height} \\
   =\frac{1}{3}(72)(8) \\
   =192 \text{ units}^3
   $$
   
2. مساحت رویۀ این هرم را بدست آورید.
   برای استفاده از فرمول مساحت رویۀ هرم، شما نیاز به مساحت قاعده (که در بخش 1 از این مسأله بدست آوردید) و مساحت وجه های مثلثی شکل، دارید. برای رسیدن به مساحت وجه ها، به سهم هرم (slant height) که در اینجا \(\overline{ZW}\) می باشد، نیاز دارید.
   
   ابتدا \(\triangle{PAW}\) را حل کنید. این یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) با وتر (\(\overline{PA}\)) که دارای \(6\) واحد طول است، می باشد؛ برای رسیدن به ساق ها، وتر را بر \(\sqrt{2}\) تقسیم می کنید (یا از قضیۀ فیثاغورث استفاده می کنید). \(\frac{6}{\sqrt{2}}=3\sqrt{2}\) ، بنابراین \(\overline{PW}\) و \(\overline{AW}\) هر دو دارای طول \(3\sqrt{2}\) می باشند. اکنون می توانید با استفاده از قضیۀ فیثاغورث، با هر کدام از دو مثلث قائم الزاویۀ \(\triangle{PZW}\) یا \(\triangle{AZW}\)، طول \(\overline{ZW}\) را بدست آورید. انتخابتان را انجام بدهید. \(\triangle{AZW}\) چطور است؟
   $$
   (ZW)^2=(AZ)^2+(AW)^2 \\
   =8^2+(3\sqrt{2})^2 \\
   =64+18 \\
   =82 \\
   ZW=\sqrt{82}
   $$
   اکنون شما آماده اید که با استفاده از فرمول مساحت رویه این مسأله را به پایان برسانید. (یک حقیقت دیگر که شما نیاز دارید اینست که \(\overline{PV}\) برابر با \(6\sqrt{2}\) می باشد، زیرا دو برابر \(\overline{PW}\) است.)
   $$
   \text{SA}_{\text{Pyramid}} = \text{area}_{\text{base}} + \text{lateral area}_{\text{four triangles}} \\
   =72+4(\frac{1}{2} \text{base} \cdot \text{slant height}) \\
   = 72+4(\frac{1}{2} \cdot 6\sqrt{2} \cdot \sqrt{82}) \\
   = 72+12 \sqrt{164} \\
   =72+24\sqrt{41} \\
   \approx 225.7 \text{ units}^2
   $$
   تمام شد.
   

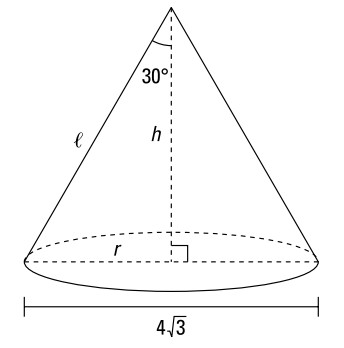
اکنون به سراغ یک مسالۀ مخروط می رویم:

داده ها:
مخروط با قطر قاعدۀ \(4\sqrt{3}\)
زاویۀ بین ارتفاع مخروط و مولد مخروط (slant height) برابر با \(30^{\circ}\) می باشد
پیدا کنید:

1. حجم این مخروط
   
2. مساحت رویۀ این مخروط
   

1. حجم این مخروط را بیابید.
   برای محاسبۀ حجم این مخروط، به ارتفاع و شعاع قاعدۀ آن نیاز دارید. مسلماً شعاع آن نصفِ قطرش یعنی برابر با \(2\sqrt{3}\) می باشد. سپس، از آنجایی که ارتفاع بر قاعده عمود می باشد، مثلثی که توسط شعاع، ارتفاع، و مولد مخروط شکل گرفته است، یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) می باشد. شما می توانید ببینید که \(h\) ساق بزرگتر و \(r\) ساق کوچکتر این مثلث می باشد، بنابراین برای بدست آوردن \(h\)، شما \(r\) را در \(\sqrt{3}\) ضرب می کنید (فصل 8 را ببینید):
   $$ h=\sqrt{3} \cdot 2\sqrt{3} = 6 $$
   شما برای استفاده از فرمول حجم مخروط آماده اید:
   $$
   \text{Vol}_{\text{Cone}}=\frac{1}{3}\text{area}_{\text{base}} \cdot \text{height} \\
   =\frac{1}{3} \pi r^2 \cdot h \\
   =\frac{1}{3} \pi (2\sqrt{3})^2 \cdot 6 \\
   =24 \pi \\
   \approx 75.4 \text{ units}^3
   $$
   
2. مساحت رویۀ این مخروط را بیابید.
   برای مساحت رویه، تنها چیز دیگری که نیاز دارید، مولد مخروط (\(\ell\)) می باشد. مولد مخروط وتر این مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است، پس صرفاً دوبرابر شعاع می باشد، که \(4\sqrt{3}\) می شود. اکنون همه چیز را در فرمول مساحت رویۀ مخروط، جایگذاری کنید:
   $$
   \text{SA}_{\text{Cone}} = \text{area}_{\text{base}} + \text{lateral area}_{\text{triangle}} \\
   =\pi r^2 + {1\over2} (\text{base}) (\text{slant height}) \\
   =\pi r^2 + {1\over2} (2\pi r) (\ell) \\
   =\pi (2\sqrt{3})^2 + {1\over2} (2\pi \cdot 2\sqrt{3}) (4\sqrt{3}) \\
   = 12 \pi + 24 \pi \\
   =36 \pi \\
   \approx 113.1 \text{ units}^2
   $$