خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تبدیل توابع (Transforming Functions)

توابع و تمامی ویژگیها، مشخصات، و چیزهای عجیب و غریب آنها، از علاقه مندیهای ریاضیدانان و سایر کسانی که از آنها به عنوان مدل هایی برای برنامه های کاربردی استفاده می کنند، می باشند. استفاده از توابع برای یافتن مقادیر یا پاسخ های مسأله های کاربردی تنها در صورتی سودمند است که پیچاندن یا اندکی تغییر دادن آن توابع به اندازۀ کافی ساده باشد. تغییرات قابل پیش بینی و کنترل شده در توابع این نیاز به سادگی و سهولت را به طور کامل برطرف می کنند. در فصل 22 در مورد چگونگی تاثیر این تبدیلات بر روی توابع مثلثاتی بحث شده است. در این بخش، یک توضیحات کلی تر از چگونگی پیچاندن توابع ارائه شده است.

انتقال (translation) یک لغزیدن است، که به این معناست که آن تابع به لحاظ گرافیکی همان شکل را دارد، اما نمودار آن تابع به محلی بالاتر یا پایینتر از محل قبلی، یا به سمت چپ یا راست سُر می خورد، و در موقعیت دیگری بر روی صفحۀ مختصات قرار می گیرد.
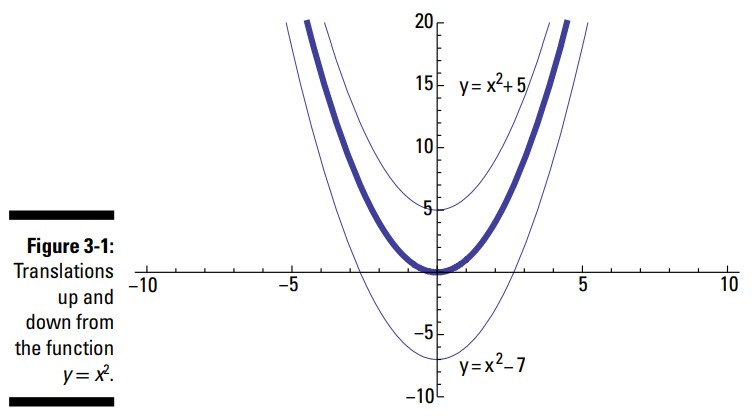
شکل 1-3 سهمیِ \(y=x^2\) را با یک انتقال \(5\) واحدی رو به سمت بالا و یک انتقال \(7\) واحدی رو به سمت پایین نشان می دهد. سهمی (شلجمی) نمودار یک چندجمله ایِ درجه دوم می باشد، که به معنای اینست که آن چندجمله ای دارای توانی از \(2\) در یکی از نماهایش می باشد. این نمودار یک منحنیِ زیبای U شکل را می سازد.
در مورد تابعی فکر کنید که شما برای تعیین اینکه یک شخص به ازاء تعداد ساعات خاصی کار کردن، چقدر پول بدست می آورد، از آن استفاده می کنید. اگر شما یک پاداش به آن بیفزایید، یا یک جریمه را از آن کسر کنید، این مبلغ می تواند رو به سمت بالا یا پایین به نرمی حرکت کند (بلغزد). در اینجا چگونگی این وضعیت را در نماد تابع می بینید:
شخصی که به ازاء هر ساعت \(8$\) می گیرد اما یک پاداش \(50$\) دریافت می کند دارای یک تابع پرداخت برای \(h\) ساعت می باشد که اینگونه است: \(P(h)=8h+50\) . اگر همان شخص به خاطر تاخیرش \(6$\) جریمه گردد، تابع پرداخت اینگونه خواهد بود: \(P(h)=8h-6\) .
شکل 2-3 سهمی \(y=x^2\) را با یک انتقال \(5\) واحدی به سمت راست و یک انتقال \(7\) واحدی رو به سمت چپ نشان می دهد.

اگر از تابعی برای تعیین میزان کمیسیون یک شخص که برای فروش تعداد معینی از کامپیوتر دریافت می کند، استفاده کنید، هنگامی که شما تعداد واحدهایی که آن شخص نیاز به فروش دارد را اضافه یا کم می کنید، این کمیسیون می تواند تحت تاثیر قرار بگیرد. در اینجا چگونگی این وضعیت در نماد تابع را داریم:
شخصی که به ازاء هر کامپیوتری که می فروشد \(50$\) کمیسیون می گیرد، اما به عنوان یک مشوق پیشاپیش برای دو کامپیوتر اعتبار دریافت می کند، دارای یک تابع کمیسیون برای \(x\) کامپیوتر به این شکل می باشد: \(P(x)=50(x+2)\) . از سوی دیگر، شخصی که دارای جدول کمیسیون یکسانی می باشد اما باید دو کامپیوتر را پس بدهد و با یک کسری بودجه آغاز می کند دارای یک تابع کمیسیون به این شکل می باشد: \(P(x)=50(x-2)\) .
دو نوع از تبدیل ها مشابه بازتاب ها و چرخش ها عمل می کنند. یک تبدیل تمامی خروجی های مثبت را به مقادیر منفی و تمامی مقادیر منفی را به مقادیر مثبت تبدیل می کند. تبدیل دیگر ورودی های را معکوس می کند ـــ مثبت به منفی و منفی به مثبت.
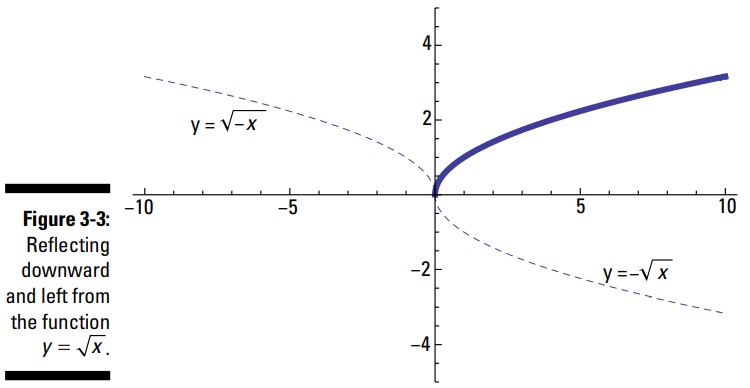
شکل 3-3 بازتاب های تابع \(y=\sqrt{x}\) را نشان می دهد. بازتاب رو به سمت پایین، تمامی نقاط را زیر محور \(x\) قرار می دهد. بازتاب به سمت چپ تمامی مقادیر ورودی را به سمت چپ محور \(y\) منتقل می کند. با وجود اینکه به نظر می رسد که منفی ها نباید زیر رادیکال قرار بگیرند، در واقع، منفی قرار گرفته قبل از \(x\) بدین معنا می باشد که شما معکوس تمامی \(x\) های منفی را بدست می آورید ـــ که آنها را تبدیل به مثبت می کند.
توصیف بازتاب های رو به سمت چپ و راست، به لحاظ عملی اندکی مشکل تر می باشد. این یکی را برای اندازه امتحان کنید: اگر یک تابع به شما بگوید یک دستگاه در تعداد ساعات معینی چند آیتم می تواند تولید کند، آن گاه وارد کردن مقادیر منفی به شما کمک می کند تا تعیین کنید چقدر باید به عقب بازگردید تا آن تعداد از آیتم ها توسط آن تاریخ و زمان تولید شوند.

انتقال یک تابع (Translating a function)
انتقال (translation) یک لغزیدن است، که به این معناست که آن تابع به لحاظ گرافیکی همان شکل را دارد، اما نمودار آن تابع به محلی بالاتر یا پایینتر از محل قبلی، یا به سمت چپ یا راست سُر می خورد، و در موقعیت دیگری بر روی صفحۀ مختصات قرار می گیرد.
لغزیدن رو به بالا یا پایین
شکل 1-3 سهمیِ \(y=x^2\) را با یک انتقال \(5\) واحدی رو به سمت بالا و یک انتقال \(7\) واحدی رو به سمت پایین نشان می دهد. سهمی (شلجمی) نمودار یک چندجمله ایِ درجه دوم می باشد، که به معنای اینست که آن چندجمله ای دارای توانی از \(2\) در یکی از نماهایش می باشد. این نمودار یک منحنیِ زیبای U شکل را می سازد.

در مورد تابعی فکر کنید که شما برای تعیین اینکه یک شخص به ازاء تعداد ساعات خاصی کار کردن، چقدر پول بدست می آورد، از آن استفاده می کنید. اگر شما یک پاداش به آن بیفزایید، یا یک جریمه را از آن کسر کنید، این مبلغ می تواند رو به سمت بالا یا پایین به نرمی حرکت کند (بلغزد). در اینجا چگونگی این وضعیت را در نماد تابع می بینید:
-
انتقال رو به بالا به میزان \(C\) واحد: \(f(x)+C\)
-
انتقال رو به پایین به میزان \(C\) واحد: \(f(x)-C\)
شخصی که به ازاء هر ساعت \(8$\) می گیرد اما یک پاداش \(50$\) دریافت می کند دارای یک تابع پرداخت برای \(h\) ساعت می باشد که اینگونه است: \(P(h)=8h+50\) . اگر همان شخص به خاطر تاخیرش \(6$\) جریمه گردد، تابع پرداخت اینگونه خواهد بود: \(P(h)=8h-6\) .
لغزش رو به سمت چپ یا راست
شکل 2-3 سهمی \(y=x^2\) را با یک انتقال \(5\) واحدی به سمت راست و یک انتقال \(7\) واحدی رو به سمت چپ نشان می دهد.

اگر از تابعی برای تعیین میزان کمیسیون یک شخص که برای فروش تعداد معینی از کامپیوتر دریافت می کند، استفاده کنید، هنگامی که شما تعداد واحدهایی که آن شخص نیاز به فروش دارد را اضافه یا کم می کنید، این کمیسیون می تواند تحت تاثیر قرار بگیرد. در اینجا چگونگی این وضعیت در نماد تابع را داریم:
-
انتقال به سمت چپ به میزان \(C\) واحد: \(f(x+C)\)
-
انتقال به سمت راست به میزان \(C\) واحد: \(f(x-C)\)
شخصی که به ازاء هر کامپیوتری که می فروشد \(50$\) کمیسیون می گیرد، اما به عنوان یک مشوق پیشاپیش برای دو کامپیوتر اعتبار دریافت می کند، دارای یک تابع کمیسیون برای \(x\) کامپیوتر به این شکل می باشد: \(P(x)=50(x+2)\) . از سوی دیگر، شخصی که دارای جدول کمیسیون یکسانی می باشد اما باید دو کامپیوتر را پس بدهد و با یک کسری بودجه آغاز می کند دارای یک تابع کمیسیون به این شکل می باشد: \(P(x)=50(x-2)\) .
بازتاب شبیه یک آینه
دو نوع از تبدیل ها مشابه بازتاب ها و چرخش ها عمل می کنند. یک تبدیل تمامی خروجی های مثبت را به مقادیر منفی و تمامی مقادیر منفی را به مقادیر مثبت تبدیل می کند. تبدیل دیگر ورودی های را معکوس می کند ـــ مثبت به منفی و منفی به مثبت.
-
بازتاب رو به سمت بالا و پایین (خروجی ها تغییر می کنند): \(-f(x)\)
-
بازتاب رو به سمت چپ و راست (ورودی ها تغییر می کنند): \(f(-x)\)
شکل 3-3 بازتاب های تابع \(y=\sqrt{x}\) را نشان می دهد. بازتاب رو به سمت پایین، تمامی نقاط را زیر محور \(x\) قرار می دهد. بازتاب به سمت چپ تمامی مقادیر ورودی را به سمت چپ محور \(y\) منتقل می کند. با وجود اینکه به نظر می رسد که منفی ها نباید زیر رادیکال قرار بگیرند، در واقع، منفی قرار گرفته قبل از \(x\) بدین معنا می باشد که شما معکوس تمامی \(x\) های منفی را بدست می آورید ـــ که آنها را تبدیل به مثبت می کند.

نکات فنی: یک صندوق پول (صندوقی که در فروشگاه ها قرار می دهند) می تواند با گرفتن مقادیر کوپن ها که فروشنده آنها را وارد می کند یا اسکن می کند، ورودی ها را به اعداد (منفی) معکوسشان تبدیل کند، قبل از اینکه صندوق محاسبات نهایی را انجام بدهد، این تبدیل به مقادیر منفی صورت می پذیرد. نمودار این فرآیند به عنوان یک بازتاب رو به سمت پایین از مثبت به منفی، عمل می کند.
توصیف بازتاب های رو به سمت چپ و راست، به لحاظ عملی اندکی مشکل تر می باشد. این یکی را برای اندازه امتحان کنید: اگر یک تابع به شما بگوید یک دستگاه در تعداد ساعات معینی چند آیتم می تواند تولید کند، آن گاه وارد کردن مقادیر منفی به شما کمک می کند تا تعیین کنید چقدر باید به عقب بازگردید تا آن تعداد از آیتم ها توسط آن تاریخ و زمان تولید شوند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: