خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توابع رایج و نمودار آنها

شما در مطالعۀ حسابان هزاران تابع خواهید دید، بنابراین فکر بدی نیست که خودتان را با توابع اصلی در این بخش آشنا کنید: خط (line)، سهمی (parabola)، تابع قدر مطلق (absolute value)، توابع مکعبی (cubing) و ریشۀ سوم (cube root)، و توابع نمایی (exponential) و توابع لگاریتمی (logarithmic).

یک خط ساده ترین تابعی است که می توانید نمودارش را بر روی صفحۀ مختصات ترسیم کنید. (خطها در حسابان حائز اهمیت هستند زیرا معمولاً خطهایی را مورد بررسی قرار می دهید که تانژانت منحنی ها می باشند و زیرا هنگامی که به اندازۀ کافی یک منحنی را بزرگنمایی کنید، شبیه یک خط خواهد بود و همانند خط رفتار خواهد کرد.) شکل 8-5 مثالی از یک خط را به شما نشان می دهد:
$$y=3x+5$$
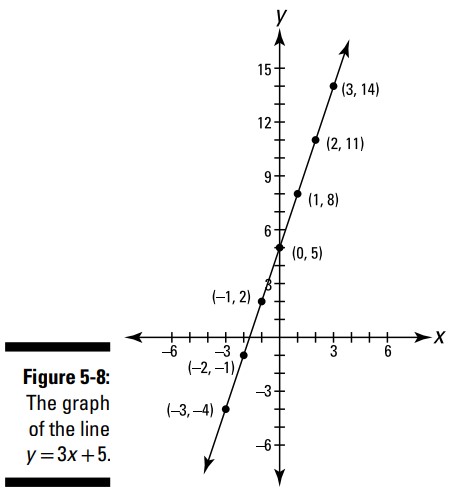
مهمترین چیز در مورد خط موجود در شکل 8-5 ـــ دست کم برای مطالعات حسابان شما ـــ شیب یا تندی آن می باشد. توجه داشته باشید هرگاه که \(x\) به اندازۀ \(1\) واحد به سمت راست می رود، \(y\) به میزان \(3\) واحد بالا می رود. یک روش خوب برای بصری کردن شیب خط اینست که یک پلکان زیر این خط رسم کنید (شکل 9-5 را ببینید). بخش عمودی این پله rise، و بخش افقی آن run نامیده می شود، و شیب آن به شکل نسبتی بین rise بر روی run تعریف می شود:
$$\text{Slope}=\frac{\text{rise}}{\text{run}}=\frac{3}{1}=3$$
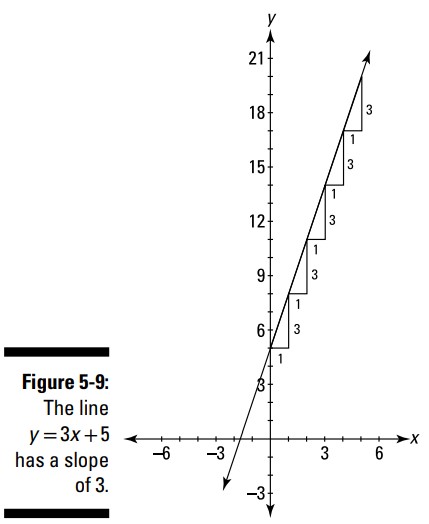
شما مجبور نیستید تا run را برابر با \(1\) قرار دهید. نسبت بین rise به run، و از اینرو شیب، صرفنظر از اینکه پله ها را به چه اندازه ای بسازید، همیشه یکسان خواهد بود. با این حال، اگر run را برابر با \(1\) بسازید، شیب با rise برابر خواهد بود، زیرا هر عددی تقسیم بر \(1\) خودش می شود. این یک روش خوب برای فکر کردن به شیب می باشد ـــ شیب میزان بالا رفتن یا پایین رفتن یک خط است در صورتی که \(1\) واحد رو به سمت راست می رود.
در اینجا فرمول شیب خط را داریم:
$$\text{Slope} = \frac{y_2 - y_1}{x_2 - x_1}$$
هر دو نقطۀ دلخواهی را بر روی خط موجود در شکل 9-5 در نظر بگیرید، به عنوان مثال \((1,8)\) و \((3,14)\)، و آنها را در این فرمول جایگذاری کنید تا شیب این خط را محاسبه کنید:
$$\text{Slope} = \frac{14-8}{3-1}=\frac{6}{2}=3$$
این محاسبه به یک معنا شامل یک مرحله از پلکان است که \(2\) واحد رو به جلو و \(6\) واحد رو به بالا می رود. پاسخ \(3\) با شیبی که در شکل 9-5 می بینید، مطابقت دارد.
هر خطی موازی با این خط دارای شیب یکسانی می باشد، و هر خطی عمود بر این خط دارای شیب \(-\frac{1}{3}\)، که قرینۀ کسرمتقابل (opposite reciprocal) \(3\) است، می باشد.
اگر معادلۀ خط \(y=3x+5\) را داشته باشید، اما نمودارش را نداشته باشید، می توانید نمودار این خط را با روش از مد افتادۀ دستی، یا با ماشین حساب نموداریتان، ترسیم کنید. روش از مد افتادۀ دستی اینست که جدولی از مقادیر بسازید که در آن مقادیری را در \(x\) جایگذاری می کنید و مقدار \(y\) را محاسبۀ می نمایید. اگر \(0\) را در \(x\) جایگذاری کنید، \(y\) برابر با \(5\) خواهد بود؛ \(1\) را در \(x\) جایگذاری کنید، و \(y\) برابر با \(8\) خواهد بود؛ \(2\) را در \(x\) جایگذاری کنید، و \(y\) برابر با \(11\) خواهد بود، و به همین ترتیب. جدول 1-5 این نتایج را نشان می دهد.
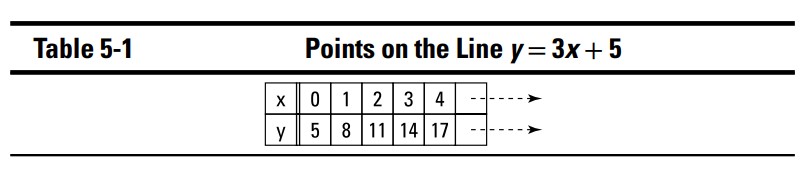
این نقاط را رسم کنید، نقطه ها را به یکدیگر متصل سازید، و فلش هایی را در دو انتهای آن قرار دهید ـــ این خط شما است. با ماشین حسابهای نموداری، این کار به سادگی یک بشکن زدن است. کافیست \(y=3x+5\) را در آن وارد کنید، و ماشین حساب شما نمودار این خط را ترسیم می کند و جدولی مشابه جدول 1-5 را تولید می کند.
شما می توانید ببینید که خط موجود در شکل 9-5 از محور \(y\) در \(5\) عبور می کند ـــ این نقطه عرض از مبدأ (y-intercept) این خط می باشد. از آنجا که هم شیب \(3\) و هم عرض از مبدأ \(5\) در معادلۀ \(y=3x+5\) ظاهر شده اند، گفته می شود که این معادله در شکل شیب تقاطع می باشد. این شکل در روش کلی به اینصورت نوشته می شود:
(اگر این شکل شیب-تقاطع برای شما آشنا نمی آید، همین الان حسابان را رها کنید و به سراغ دورۀ آموزش جبر بروید.)
همۀ خطها به استثناء خطهای عمودی می توانند در این شکل نوشته شوند. به عنوان مثال، خطهای عمودی به شکل \(x=6\) نوشته می شوند. این عدد به شما می گوید که این خط عمودی در کجا از محور \(x\) عبور می کند.
همچنین معادلۀ یک خط افقی نیز متفاوت به نظر می رسد، به عنوان مثال \(y=10\). اما به لحاظ فنی در شکل \(y=mx+b\) می گنجد ـــ از آنجا که شیب یک خط افقی برابر با صفر است، و از آنجا که صفر ضربدر \(x\) برابر با صفر می شود، هیچ جملۀ \(x\) داری در این معادله وجود ندارد. اما اگر بخواهید امتحانش کنید، می توانید \(y=10\) را به شکل \(y=0x+10\) بنویسید.
اگر \(m=1\) و \(b=0\) باشد، شما تابع \(y=x\) را بدست خواهید آورد. این خط از مبدأ \((0,0)\) عبور می کند و با هر دو محور مختصات یک زاویۀ \(45^{\circ}\) را تشکیل می دهد. این تابع، تابع همانی (identity function) نامیده می شود، زیرا خروجی آن با ورودی آن برابر است.
برای استفاده از این شکل، شما نیاز به دانستن یک نقطه (point) بر روی یک خط و دانستن شیب آن خط دارید. شما می توانید از هر نقطه ای بر روی این خط استفاده کنید. دوباره خط موجود در شکل 9-5 را در نظر بگیرید. هر نقطۀ دلخواه را انتخاب کنید، فرض کنید \((2,11)\)، و سپس مختصات \(x\) و \(y\) آن را در \(x_1\) و \(y_1\) جایگذاری کنید، و شیب \(3\) را در \(m\) جایگذاری کنید:
$$y-11=3(x-2)$$
با اندکی جبر، می توانید این معادله را به معادله ای که هم اکنون می شناسیم تبدیل کنید، \(y=3x+5\). خودتان امتحان کنید.
شما باید با دو تابعی که در شکل 10-5 می بینید آشنا باشید: تابع سهمی \(f(x)=x^2\)، و تابع قدرمطلق \(g(x)=|x|\) .
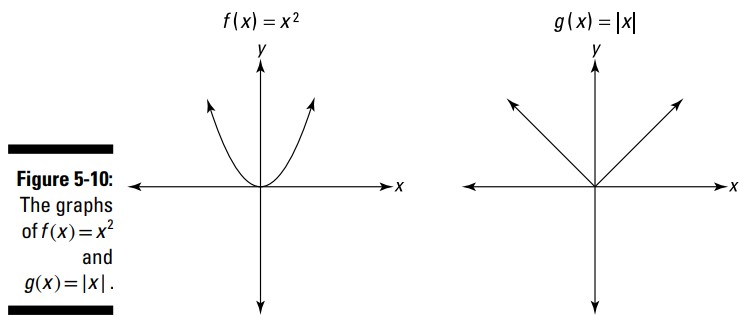
توجه کنید که هر دوی این توابع با توجه به محور \(y\) متقارن می باشند. به عبارت دیگر، سمت چپ و راست هر نمودار، تصویر آینه شدۀ دیگری می باشد. این آنها را تبدیل به توابع زوج (even functions) می کند. یک تابع چندجمله ای (polynomial function) مانند \(y=9x^4-4x^2+3\)، که در آن تمامی توانهای \(x\) زوج هستند، یک نوع از توابع زوج می باشد. (چنین تابع چندجمله ای می تواند شامل یک جملۀ ثابت مانند \(3\) در مثال قبلی می باشد ـــ اما ضرورتی ندارد. این معنادار است، زیرا \(3\) با \(3x^0\) یکسان است و صفر هم عددی زوج است.) تابع زوج دیگر \(y=\cos(x)\) می باشد (فصل 6 را ببینید).
با استفاده از ماشین حساب نموداریتان، نمودار \(f(x)=x^3\) و \(g(x)=\sqrt[3]{x}\) را ترسیم کنید. این دو تابع تقارن فرد (odd symmetry) را نشان می دهند. توابع فرد (Odd functions) با توجه به مبدأ مختصات متقارن می باشند، بدین معنا که اگر آنها را \(180^{\circ}\) پیرامون مبدأ بچرخانید، بر روی خودشان فرود خواهند آمد. یک چندجمله ای مانند \(y=4x^5-x^3+2x\)، که در آن تمامی توانهای \(x\) فرد باشند، یک نوع از توابع فرد می باشد. (برخلاف یک تابع چندجمله ایِ زوج، یک تابع چندجمله ایِ فرد، نمی تواند شامل یک جملۀ ثابت باشد.) تابع فرد دیگری \(y=\sin(x)\) می باشد (فصل 6 را ببینید).
بسیاری از توابع نه زوج و نه فرد هستند، به عنوان مثال \(y=3x^2-5x\).
یک تابع نمایی، تابعی است که دارای توانی باشد که آن توان شامل یک متغیر باشد، مانند \(f(x)=2^x\) یا \(g(x)=10^x\) . شکل 11-5 نمودار این دو تابع را در دستگاه مختصات \(\text{x-y}\) نشان می دهد.
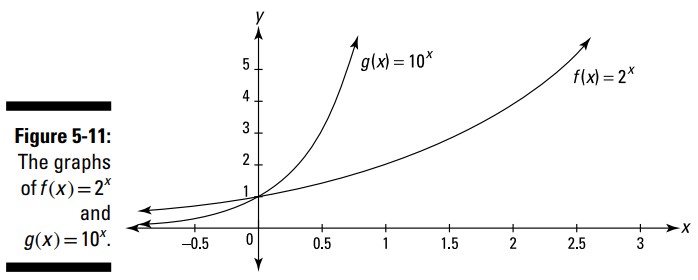
هر دوی این توابع، همانند تمامی توابع نمایی دیگر در شکل \(f(x)=b^x\)، از نقطۀ \((0,1)\) عبور می کنند. هنگامی که \(b\) بزرگتر از \(1\) باشد، شما رشد نمایی (exponential growth) دارید. تمامی اینگونه توابع بدون هیچ محدودیتی، همچنان که در جهت راست بسوی مثبت بی نهایت پیش می روند، بالا و بالاتر می روند. همچنانکه بسمت چپ و بسوی منفی بی نهایت پیش می روند، در امتداد محور \(x\) می خزند، و همیشه به آن محور نزدیکتر می شوند، اما هرگز آن را لمس نمی کنند. شما از این تابع و توابع مرتبط با آن برای شکل دادن به چیزهایی مانند سرمایه گذاریها، تورم، و رشد جمعیت، استفاده می کنید.
هنگامی که \(b\) بین \(0\) و \(1\) باشد، شما یک تابع نمایی رو به کاهش (exponential decay function) دارید. نمودار چنین تابعی مشابه برعکسِ توابع نمایی رو به رشد می باشند. همچنین توابع نمایی رو به کاهش از محور \(y\) در نقطۀ \((0,1)\) عبور می کنند، اما تا ابد رو به سمت چپ می روند، و در امتداد محور \(x\) رو به سمت راست می خزند. این توابع چیزهایی که در طول زمان کوچک می شوند را مدلسازی می کنند، مانند تجزیۀ رادیواکتیو در اورانیوم.
یک تابع لگاریتمی به سادگی یک تابع نمایی است که جای محور \(x\) و \(y\) آن عوض شده است. به عبارت دیگر، جهت بالا و پایین در یک نمودار نمایی متناظر با جهت راست و چپ در یک نمودار لگاریتمی می باشد، و جهت راست و چپ در یک نمودار نمایی متناظر با جهت بالا و پایین در یک نمودار لگاریتمی می باشد. (اگر در مورد لگاریتم نیاز به یادآوری دارید، فصل 4 را مرور کنید.) شما می توانید این ارتباط را در شکل 12-5 ، که در آن نمودارهای \(f(x)=2^x\) و \(g(x)=\log_2 x\) هر دو بر روی مجموعۀ یکسانی از محورها ترسیم شده اند، ببینید.
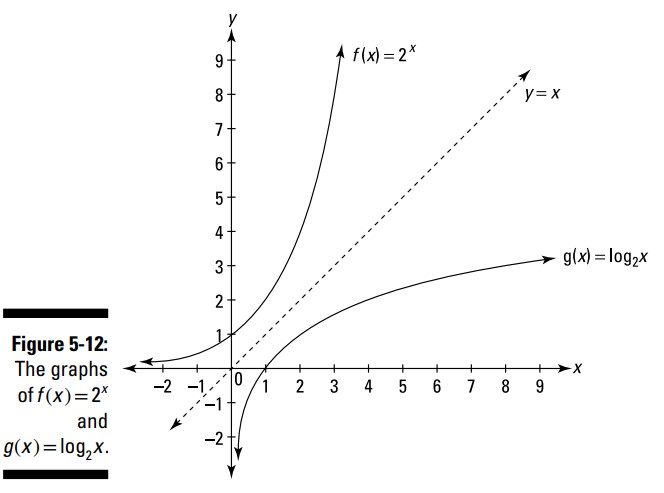
هر دویِ توابع نمایی و لگاریتمی یکنواخت (monotonic) می باشند. یک تابع یکنواخت (monotonic function) یا در سرتاسر کل دامنه اش رو به بالا می رود (که یک تابع افزایشی نامیده می شود)، یا در سرتاسر کل دامنه اش رو به پایین می رود (که یک تابع کاهشی نامیده می شود). (من در اینجا فرض می گیرم ـــ همچنانکه تقریباً همیشه همینطور است ـــ این حرکت در امتداد این تابع از سمت چپ به راست است.)
در شکل 12-5 به تقارن این دو تابع پیرامون خط \(y=x\) توجه کنید. این منجر می شود تا این دو تابع معکوس (Inverse) یکدیگر باشند، که در بخش بعدی هم به همین موضوع خواهیم پرداخت.

نمودار خطها
یک خط ساده ترین تابعی است که می توانید نمودارش را بر روی صفحۀ مختصات ترسیم کنید. (خطها در حسابان حائز اهمیت هستند زیرا معمولاً خطهایی را مورد بررسی قرار می دهید که تانژانت منحنی ها می باشند و زیرا هنگامی که به اندازۀ کافی یک منحنی را بزرگنمایی کنید، شبیه یک خط خواهد بود و همانند خط رفتار خواهد کرد.) شکل 8-5 مثالی از یک خط را به شما نشان می دهد:
$$y=3x+5$$

شیب ها (slopes)
مهمترین چیز در مورد خط موجود در شکل 8-5 ـــ دست کم برای مطالعات حسابان شما ـــ شیب یا تندی آن می باشد. توجه داشته باشید هرگاه که \(x\) به اندازۀ \(1\) واحد به سمت راست می رود، \(y\) به میزان \(3\) واحد بالا می رود. یک روش خوب برای بصری کردن شیب خط اینست که یک پلکان زیر این خط رسم کنید (شکل 9-5 را ببینید). بخش عمودی این پله rise، و بخش افقی آن run نامیده می شود، و شیب آن به شکل نسبتی بین rise بر روی run تعریف می شود:
$$\text{Slope}=\frac{\text{rise}}{\text{run}}=\frac{3}{1}=3$$

شما مجبور نیستید تا run را برابر با \(1\) قرار دهید. نسبت بین rise به run، و از اینرو شیب، صرفنظر از اینکه پله ها را به چه اندازه ای بسازید، همیشه یکسان خواهد بود. با این حال، اگر run را برابر با \(1\) بسازید، شیب با rise برابر خواهد بود، زیرا هر عددی تقسیم بر \(1\) خودش می شود. این یک روش خوب برای فکر کردن به شیب می باشد ـــ شیب میزان بالا رفتن یا پایین رفتن یک خط است در صورتی که \(1\) واحد رو به سمت راست می رود.
تعریف شیب مثبت (positive)، شیب منفی (negative)، شیب صفر (zero)، و شیب تعریف نشده (undefined): خطهایی که رو به سمت بالا و راست می روند دارای شیب مثبت هستند؛ خطهایی که رو به سمت پایین و راست می روند دارای شیب منفی هستند. خطهای افقی دارای شیب صفر می باشند، و خطهای عمودی شیب ندارند ـــ شما اینطور بیان می کنید که شیب یک خط عمودی تعریف نشده می باشد.
در اینجا فرمول شیب خط را داریم:
$$\text{Slope} = \frac{y_2 - y_1}{x_2 - x_1}$$
هر دو نقطۀ دلخواهی را بر روی خط موجود در شکل 9-5 در نظر بگیرید، به عنوان مثال \((1,8)\) و \((3,14)\)، و آنها را در این فرمول جایگذاری کنید تا شیب این خط را محاسبه کنید:
$$\text{Slope} = \frac{14-8}{3-1}=\frac{6}{2}=3$$
این محاسبه به یک معنا شامل یک مرحله از پلکان است که \(2\) واحد رو به جلو و \(6\) واحد رو به بالا می رود. پاسخ \(3\) با شیبی که در شکل 9-5 می بینید، مطابقت دارد.
هر خطی موازی با این خط دارای شیب یکسانی می باشد، و هر خطی عمود بر این خط دارای شیب \(-\frac{1}{3}\)، که قرینۀ کسرمتقابل (opposite reciprocal) \(3\) است، می باشد.
خطهای موازی (Parallel lines) دارای شیب یکسانی می باشند. خطهای متعامد (Perpendicular lines) دارای شیب قرینۀ کسرمتقابل (قرینۀ معکوس) یکدیگر می باشند.
یادداشت مترجم: کلمۀ انگلیسی reciprocal معمولاً در آموزش های ریاضیات مدارس به "معکوس" ترجمه شده است، اما بنده تعمداً در هر جایی که توانسته ام از واژۀ "کسرمتقابل" برای ترجمۀ آن استفاده کرده ام. دلیل این امر اینست که با inverse که آنهم معنای "معکوس" می دهد و از قضا در ریاضی هم فراوان استفاده شده است، اشتباه نگردد.
ترسیم نمودار خطها
اگر معادلۀ خط \(y=3x+5\) را داشته باشید، اما نمودارش را نداشته باشید، می توانید نمودار این خط را با روش از مد افتادۀ دستی، یا با ماشین حساب نموداریتان، ترسیم کنید. روش از مد افتادۀ دستی اینست که جدولی از مقادیر بسازید که در آن مقادیری را در \(x\) جایگذاری می کنید و مقدار \(y\) را محاسبۀ می نمایید. اگر \(0\) را در \(x\) جایگذاری کنید، \(y\) برابر با \(5\) خواهد بود؛ \(1\) را در \(x\) جایگذاری کنید، و \(y\) برابر با \(8\) خواهد بود؛ \(2\) را در \(x\) جایگذاری کنید، و \(y\) برابر با \(11\) خواهد بود، و به همین ترتیب. جدول 1-5 این نتایج را نشان می دهد.

این نقاط را رسم کنید، نقطه ها را به یکدیگر متصل سازید، و فلش هایی را در دو انتهای آن قرار دهید ـــ این خط شما است. با ماشین حسابهای نموداری، این کار به سادگی یک بشکن زدن است. کافیست \(y=3x+5\) را در آن وارد کنید، و ماشین حساب شما نمودار این خط را ترسیم می کند و جدولی مشابه جدول 1-5 را تولید می کند.
شیب-تقاطع (Slope-intercept) و شیب-نقطه (point-slope)
شما می توانید ببینید که خط موجود در شکل 9-5 از محور \(y\) در \(5\) عبور می کند ـــ این نقطه عرض از مبدأ (y-intercept) این خط می باشد. از آنجا که هم شیب \(3\) و هم عرض از مبدأ \(5\) در معادلۀ \(y=3x+5\) ظاهر شده اند، گفته می شود که این معادله در شکل شیب تقاطع می باشد. این شکل در روش کلی به اینصورت نوشته می شود:
شکل شیب-تقاطع (Slope-intercept form):
$$y=mx+b$$
در این شکل \(m\) برابر با شیب و \(b\) برابر با عرض از مبدأ می باشد.
$$y=mx+b$$
در این شکل \(m\) برابر با شیب و \(b\) برابر با عرض از مبدأ می باشد.
(اگر این شکل شیب-تقاطع برای شما آشنا نمی آید، همین الان حسابان را رها کنید و به سراغ دورۀ آموزش جبر بروید.)
همۀ خطها به استثناء خطهای عمودی می توانند در این شکل نوشته شوند. به عنوان مثال، خطهای عمودی به شکل \(x=6\) نوشته می شوند. این عدد به شما می گوید که این خط عمودی در کجا از محور \(x\) عبور می کند.
همچنین معادلۀ یک خط افقی نیز متفاوت به نظر می رسد، به عنوان مثال \(y=10\). اما به لحاظ فنی در شکل \(y=mx+b\) می گنجد ـــ از آنجا که شیب یک خط افقی برابر با صفر است، و از آنجا که صفر ضربدر \(x\) برابر با صفر می شود، هیچ جملۀ \(x\) داری در این معادله وجود ندارد. اما اگر بخواهید امتحانش کنید، می توانید \(y=10\) را به شکل \(y=0x+10\) بنویسید.
تعریف تابع ثابت (constant function): یک خط ساده ترین نوع تابع است، و یک خط افقی (که تابع ثابت نامیده می شود) ساده ترین نوع خط است. با این وجود در حسابان زیاد حائز اهمیت نیست، بنابراین مطمئن شوید که می دانید یک خط افقی دارای معادله ای مانند \(y=10\) است و شیب آن برابر با صفر می باشد.
اگر \(m=1\) و \(b=0\) باشد، شما تابع \(y=x\) را بدست خواهید آورد. این خط از مبدأ \((0,0)\) عبور می کند و با هر دو محور مختصات یک زاویۀ \(45^{\circ}\) را تشکیل می دهد. این تابع، تابع همانی (identity function) نامیده می شود، زیرا خروجی آن با ورودی آن برابر است.
شکل نقطه-تقاطع (Point-slope form): علاوه بر شکل شیب-تقاطع برای معادلۀ یک خط، شما همچنین باید شکل نقطه-تقاطع را نیز بشناسید:
$$y-y_1 =m(x-x_1)$$
$$y-y_1 =m(x-x_1)$$
برای استفاده از این شکل، شما نیاز به دانستن یک نقطه (point) بر روی یک خط و دانستن شیب آن خط دارید. شما می توانید از هر نقطه ای بر روی این خط استفاده کنید. دوباره خط موجود در شکل 9-5 را در نظر بگیرید. هر نقطۀ دلخواه را انتخاب کنید، فرض کنید \((2,11)\)، و سپس مختصات \(x\) و \(y\) آن را در \(x_1\) و \(y_1\) جایگذاری کنید، و شیب \(3\) را در \(m\) جایگذاری کنید:
$$y-11=3(x-2)$$
با اندکی جبر، می توانید این معادله را به معادله ای که هم اکنون می شناسیم تبدیل کنید، \(y=3x+5\). خودتان امتحان کنید.
توابع سهمی وار (Parabolic) و توابع قدرمطلق (absolute value)
شما باید با دو تابعی که در شکل 10-5 می بینید آشنا باشید: تابع سهمی \(f(x)=x^2\)، و تابع قدرمطلق \(g(x)=|x|\) .

توجه کنید که هر دوی این توابع با توجه به محور \(y\) متقارن می باشند. به عبارت دیگر، سمت چپ و راست هر نمودار، تصویر آینه شدۀ دیگری می باشد. این آنها را تبدیل به توابع زوج (even functions) می کند. یک تابع چندجمله ای (polynomial function) مانند \(y=9x^4-4x^2+3\)، که در آن تمامی توانهای \(x\) زوج هستند، یک نوع از توابع زوج می باشد. (چنین تابع چندجمله ای می تواند شامل یک جملۀ ثابت مانند \(3\) در مثال قبلی می باشد ـــ اما ضرورتی ندارد. این معنادار است، زیرا \(3\) با \(3x^0\) یکسان است و صفر هم عددی زوج است.) تابع زوج دیگر \(y=\cos(x)\) می باشد (فصل 6 را ببینید).
چندین تابع فرد
با استفاده از ماشین حساب نموداریتان، نمودار \(f(x)=x^3\) و \(g(x)=\sqrt[3]{x}\) را ترسیم کنید. این دو تابع تقارن فرد (odd symmetry) را نشان می دهند. توابع فرد (Odd functions) با توجه به مبدأ مختصات متقارن می باشند، بدین معنا که اگر آنها را \(180^{\circ}\) پیرامون مبدأ بچرخانید، بر روی خودشان فرود خواهند آمد. یک چندجمله ای مانند \(y=4x^5-x^3+2x\)، که در آن تمامی توانهای \(x\) فرد باشند، یک نوع از توابع فرد می باشد. (برخلاف یک تابع چندجمله ایِ زوج، یک تابع چندجمله ایِ فرد، نمی تواند شامل یک جملۀ ثابت باشد.) تابع فرد دیگری \(y=\sin(x)\) می باشد (فصل 6 را ببینید).
بسیاری از توابع نه زوج و نه فرد هستند، به عنوان مثال \(y=3x^2-5x\).
توابع نمایی (Exponential functions)
یک تابع نمایی، تابعی است که دارای توانی باشد که آن توان شامل یک متغیر باشد، مانند \(f(x)=2^x\) یا \(g(x)=10^x\) . شکل 11-5 نمودار این دو تابع را در دستگاه مختصات \(\text{x-y}\) نشان می دهد.

هر دوی این توابع، همانند تمامی توابع نمایی دیگر در شکل \(f(x)=b^x\)، از نقطۀ \((0,1)\) عبور می کنند. هنگامی که \(b\) بزرگتر از \(1\) باشد، شما رشد نمایی (exponential growth) دارید. تمامی اینگونه توابع بدون هیچ محدودیتی، همچنان که در جهت راست بسوی مثبت بی نهایت پیش می روند، بالا و بالاتر می روند. همچنانکه بسمت چپ و بسوی منفی بی نهایت پیش می روند، در امتداد محور \(x\) می خزند، و همیشه به آن محور نزدیکتر می شوند، اما هرگز آن را لمس نمی کنند. شما از این تابع و توابع مرتبط با آن برای شکل دادن به چیزهایی مانند سرمایه گذاریها، تورم، و رشد جمعیت، استفاده می کنید.
هنگامی که \(b\) بین \(0\) و \(1\) باشد، شما یک تابع نمایی رو به کاهش (exponential decay function) دارید. نمودار چنین تابعی مشابه برعکسِ توابع نمایی رو به رشد می باشند. همچنین توابع نمایی رو به کاهش از محور \(y\) در نقطۀ \((0,1)\) عبور می کنند، اما تا ابد رو به سمت چپ می روند، و در امتداد محور \(x\) رو به سمت راست می خزند. این توابع چیزهایی که در طول زمان کوچک می شوند را مدلسازی می کنند، مانند تجزیۀ رادیواکتیو در اورانیوم.
توابع لگاریتمی (Logarithmic functions)
یک تابع لگاریتمی به سادگی یک تابع نمایی است که جای محور \(x\) و \(y\) آن عوض شده است. به عبارت دیگر، جهت بالا و پایین در یک نمودار نمایی متناظر با جهت راست و چپ در یک نمودار لگاریتمی می باشد، و جهت راست و چپ در یک نمودار نمایی متناظر با جهت بالا و پایین در یک نمودار لگاریتمی می باشد. (اگر در مورد لگاریتم نیاز به یادآوری دارید، فصل 4 را مرور کنید.) شما می توانید این ارتباط را در شکل 12-5 ، که در آن نمودارهای \(f(x)=2^x\) و \(g(x)=\log_2 x\) هر دو بر روی مجموعۀ یکسانی از محورها ترسیم شده اند، ببینید.

هر دویِ توابع نمایی و لگاریتمی یکنواخت (monotonic) می باشند. یک تابع یکنواخت (monotonic function) یا در سرتاسر کل دامنه اش رو به بالا می رود (که یک تابع افزایشی نامیده می شود)، یا در سرتاسر کل دامنه اش رو به پایین می رود (که یک تابع کاهشی نامیده می شود). (من در اینجا فرض می گیرم ـــ همچنانکه تقریباً همیشه همینطور است ـــ این حرکت در امتداد این تابع از سمت چپ به راست است.)
در شکل 12-5 به تقارن این دو تابع پیرامون خط \(y=x\) توجه کنید. این منجر می شود تا این دو تابع معکوس (Inverse) یکدیگر باشند، که در بخش بعدی هم به همین موضوع خواهیم پرداخت.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: