خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
دایره واحد (Unit Circle)

SohCahToa فقط در مثلث های قائم الزاویه درست جواب می دهد، و بنابراین فقط می تواند زوایای حاده (acute angles) را مدیریت کند ـــ زوایایی کمتر از \(90^{\circ}\) . (مجموع زوایای یک مثلث باید برابر با \(180^{\circ}\) گردد، از آنجا که یک مثلث قائم الزاویه یک زاویۀ \(90^{\circ}\) دارد، هر کدام از دو زاویۀ دیگر آن باید کمتر از \(90^{\circ}\) باشند.) اگرچه در دایرۀ واحد، شما می توانید مقادیر توابع مثلثاتی برای زوایایی با هر اندازه را بیابید. دایرۀ واحد دارای شعاعی برابر با یک واحد می باشد که در دستگاه مختصات \(\text{x-y}\) به شکلی قرار گرفته است که مرکز آن در مبدأ مختصات باشد. شکل 3-6 را ببینید.

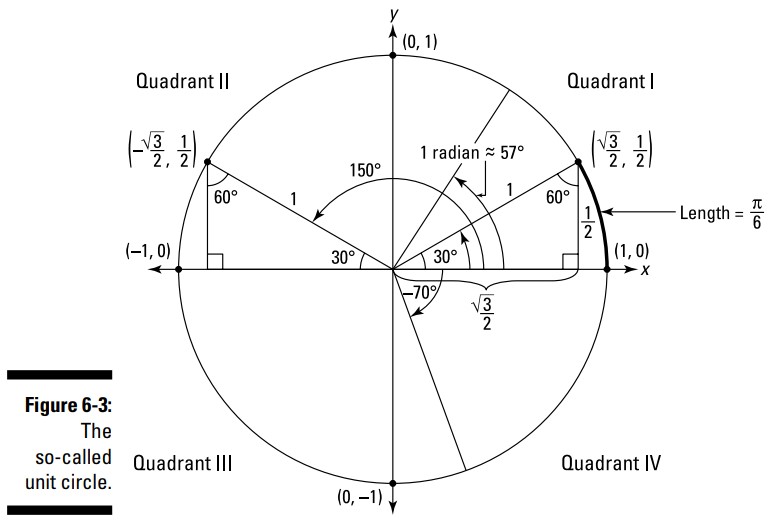
به عنوان مثال، زاویۀ \(150^{\circ}\) در شکل 3-6 از محور \(x\) مثبت آغاز می شود و در پاره خطی خاتمه می یابد که این دایرۀ واحد را در \(\biggl(-\frac{\sqrt{3}}{2},\frac{1}{2}\biggr)\) قطع می کند. اگر به جای آن در جهت ساعت گرد پیش بروید، به زاویه ای با اندازۀ منفی (مانند زاویۀ \(-70^{\circ}\) که در این شکل می بینید) می رسید.
شما همه چیز را در مورد درجه ها (degrees) می دانید. شما می دانید که زوایای \(45^{\circ}\) و \(90^{\circ}\) چه شکلی هستند؛ شما می دانید که چگونه یک چرخش \(180^{\circ}\) درجه ای را انجام بدهید و چگونه از آن نقطه با یک چرخش \(180^{\circ}\) درجه ای دیگر، یعنی مجموعاً با \(360^{\circ}\) درجه چرخش، به محل آغازین برسید.
اما درجه ها تنها واحد اندازه گیری زوایا نیستند. شما همچنین می توانید از رادیان ها (radians) نیز استفاده کنید. درجه ها و رادیان ها صرفاً دو روش متفاوت برای اندازه گیری زوایا می باشند، مانند اینچ ها و سانتیمترها که دو روش متفاوت برای اندازه گیری طول می باشند.
به زاویۀ \(30^{\circ}\) در ربع صفحۀ اول (quadrant I) از شکل 3-6 بنگرید. آیا می توانید بخش پررنگ شده از محیط این دایره را که توسط آن زاویه جدا شده است، ببینید. از آنجا که یک دایرۀ کامل برابر با \(360^{\circ}\) می باشد، آن زاویۀ \(30^{\circ}\) برابر با یک دوازدهم این دایره می باشد. بنابراین طول این کمان پررنگ شده برابر با یک دوازدهم از محیط این دایره می باشد. محیط دایره (Circumference) با فرمول \(C=2\pi r\) تعیین می شود. این دایره دارای شعاع \(1\) می باشد، بنابراین محیط آن برابر با \(2\pi\) است. از آنجا که این کمان پررنگ شده برابر با یک دوازدهم آن است، طول آن برابر با \(\frac{\pi}{6}\) می باشد، که اندازۀ رادیان این زاویۀ \(30^{\circ}\) است.
اگر بر روی این واقعیت متمرکز شوید که \(180^{\circ}\) درجه برابر با \(\pi\) رادیان است، بدست آوردن معادل رادیان سایر زوایا آسان است:
در ضمن، کلمۀ radian (رادیان) از radius (شعاع) می آید. دوباره به شکل 3-6 بنگرید. زاویه ای با اندازۀ \(1\) رادیان (در حدود \(57^{\circ}\)) کمانی را از دایره جدا می کند که طول آن برابر با شعاع آن دایره است. این مسأله نه تنها درمورد دایرۀ واحد، بلکه در مورد دایره هایی با هر اندازۀ دیگر نیز صدق می کند. به عبارت دیگر، شعاع هر دایره ای را بگیرید، آن را در امتداد محیط دایره قرار دهید، و کمان حاصل از آن برابر با \(1\) رادیان خواهد بود.
دوباره، به دایرۀ واحد در شکل 3-6 بنگرید. آیا مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) را در ربع صفحۀ اول می بینید؟ این مثلث با مثلثی که در شکل 2-6 (در آموزش قبلی) دیدید هم شکل است اما اندازه اش نصف آن است. هر کدام از این اضلاع نصف آن طول را دارند. از آنجا که وتر آن هم اکنون دارای طول \(1\) می باشد، و از آنجا که وقتیکه \(H\) برابر با \(1\) باشد، \(\frac{O}{H}\) برابر با \(O\) می شود، سینوس این زاویۀ \(30^{\circ}\)، که برابر با \(\frac{O}{H}\) است، برابر با طول ضلع مقابل خواهد بود. ضلع مقابل برابر با \(\frac{1}{2}\) است، بنابراین این سینوس \(30^{\circ}\) است. توجه داشته باشید که طول ضلع روبرو با مختصات \(y\) در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) یکسان است. اگر کسینوس زاویۀ \(30^{\circ}\) را در این مثلث را محاسبه کنید، برابر با طول ضلع مجاور خواهد شد، که با مختصات \(x\) در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) یکسان است. توجه کنید که این مقادیر برای سینوس \(30^{\circ}\) و کسینوس \(30^{\circ}\) با مقادیری که با مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در شکل 2-6 معین شده بودند، یکسان است. این به شما نشان می دهد که کوچک کردن یا بزرگ کردن یک مثلث قائم الزاویه تاثیری بر مقادیر مثلثاتی زوایای آن مثلث ندارد.
اکنون به مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ دوم (quadrant II) در شکل 3-6 بنگرید. از آنجا که این مثلث با مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ اول، که دایره را در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) قطع کرده بود، هم اندازه است، این مثلث دوم نیز دایره را در نقطه ای که مستقیم روبروی آن قرار دارد و با نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) متقارن است، قطع می کند. مختصات این نقطه در ربع صفحۀ دوم برابر با \(\biggl( -\frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) است. اما یادتان باشد که زوایا در دایرۀ واحد همگی از محور \(x\) مثبت اندازه گیری می شوند، بنابراین وتر این مثلث قائم الزاویه یک زاویۀ \(150^{\circ}\) را می سازد؛ و این زاویه، با نقطۀ \(\biggl( -\frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) مرتبط است. کسینوس \(150^{\circ}\) که با مختصات \(x\) این نقطه تعیین می شود، \(-\frac{\sqrt{3}}{2}\) ، و سینوس \(150^{\circ}\) درجه، برابر با مختصات \(y\)، یعنی \(\frac{1}{2}\) است.
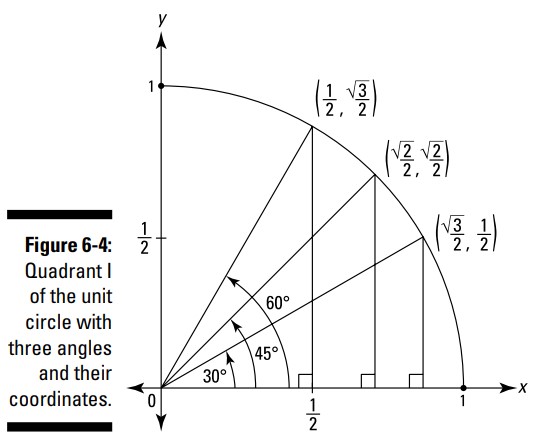
به شکل 4-6 بنگرید. حالا که همه چیز را در مورد مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می دانید، به سادگی می توانید بدست آورید که این مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) در ربع صفحۀ اول، دایرۀ واحد را در \(\biggl( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \biggr)\) قطع می کند. و اگر مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ اول را بگیرید که این دایرۀ واحد را در \(-\frac{\sqrt{3}}{2}\) قطع می کند و آن را سروته کنید، به مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) دیگری می رسید که این دایره را در \(\biggl( \frac{1}{2},\frac{\sqrt{3}}{2} \biggr)\) قطع می کند. همانطور که می توانید ببینید، این نقطه همان مختصات زاویۀ \(30^{\circ}\) درجه را به شکل معکوس شده دارد.
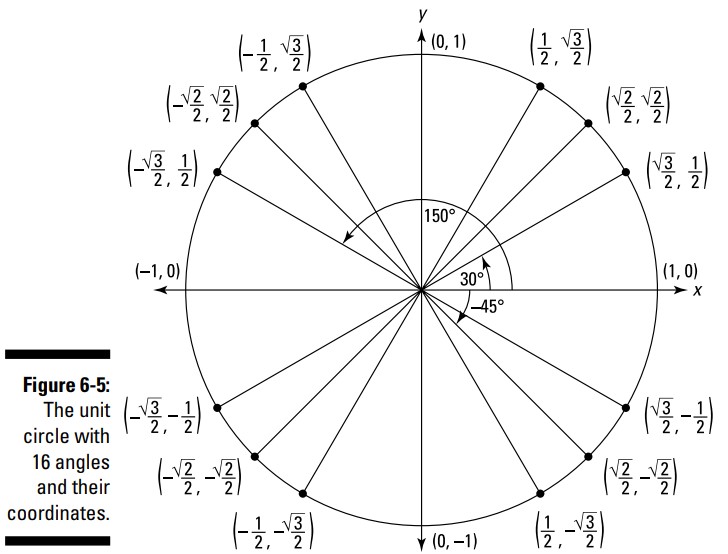
حالا به سراغ کلیت ماجرا می رویم. به دلیل تقارن در هر چهار ربع صفحه، این سه نقطه در ربع صفحۀ اول در شکل 4-6 دارای همتایانی در سایر سه ربع صفحۀ دیگر می باشند، که مجموعاً \(12\) نقطۀ شناخته شده را به شما می دهند. چهار نقطۀ قرار گرفته بر روی محورها، یعنی \((1,0)\)، \((0,1)\)، \((-1,0)\)، و \((0,-1)\) را به اینها اضافه کنید، و در مجموع \(16\) نقطه خواهید داشت، که هر کدام از آنها به یک زاویه مرتبط است، شکل 5-6 را ببینید.
این \(16\) جفت از مختصات ها، به صورت اتوماتیک کسینوس و سینوس \(16\) زاویه را به شما می دهند. و از آنجا که \(\tan \theta = \frac{\sin \theta}{\cos \theta}\)، می توانید تانژانت این \(16\) زاویه را با تقسیم مختصات \(y\) یک زاویه بر مختصات \(x\) آن بدست آورید. (توجه داشته باشید، هرگاه که کسینوس یک زاویه برابر با صفر باشد، تانژانت آن تعریف نشده خواهد بود، زیرا شما نمی توانید عددی را بر صفر تقسیم کنید.) در نهایت، می توانید کسکانت، سکانت، و کتانژانت این \(16\) زاویه را نیز بیابید، زیرا این توابع مثلثاتی صرفاً کسرمتقابل سینوس، کسینوس، و تانژانت می باشند. (همان هشدار: هرگاه که سینوس، کسینوس، و تانژانت برابر با صفر باشند، توابع معکوس آنها تعریف نشده خواهند بود.)


زوایا در دایرۀ واحد
اندازه گیری زوایا: برای اندازه گیری یک زاویه در دایرۀ واحد، از محور \(x\) مثبت آغاز کنید و به صورت پادساعت گرد به ضلع نهایی (terminal side) آن زاویه بروید.
به عنوان مثال، زاویۀ \(150^{\circ}\) در شکل 3-6 از محور \(x\) مثبت آغاز می شود و در پاره خطی خاتمه می یابد که این دایرۀ واحد را در \(\biggl(-\frac{\sqrt{3}}{2},\frac{1}{2}\biggr)\) قطع می کند. اگر به جای آن در جهت ساعت گرد پیش بروید، به زاویه ای با اندازۀ منفی (مانند زاویۀ \(-70^{\circ}\) که در این شکل می بینید) می رسید.
اندازه گیری زوایا با رادیان
شما همه چیز را در مورد درجه ها (degrees) می دانید. شما می دانید که زوایای \(45^{\circ}\) و \(90^{\circ}\) چه شکلی هستند؛ شما می دانید که چگونه یک چرخش \(180^{\circ}\) درجه ای را انجام بدهید و چگونه از آن نقطه با یک چرخش \(180^{\circ}\) درجه ای دیگر، یعنی مجموعاً با \(360^{\circ}\) درجه چرخش، به محل آغازین برسید.
اما درجه ها تنها واحد اندازه گیری زوایا نیستند. شما همچنین می توانید از رادیان ها (radians) نیز استفاده کنید. درجه ها و رادیان ها صرفاً دو روش متفاوت برای اندازه گیری زوایا می باشند، مانند اینچ ها و سانتیمترها که دو روش متفاوت برای اندازه گیری طول می باشند.
تعریف رادیان (radian): واحد رادیان در یک زاویه برابر با طول کمان در امتداد محیط دایرۀ واحد می باشد که که توسط آن زاویه بریده شده است.
به زاویۀ \(30^{\circ}\) در ربع صفحۀ اول (quadrant I) از شکل 3-6 بنگرید. آیا می توانید بخش پررنگ شده از محیط این دایره را که توسط آن زاویه جدا شده است، ببینید. از آنجا که یک دایرۀ کامل برابر با \(360^{\circ}\) می باشد، آن زاویۀ \(30^{\circ}\) برابر با یک دوازدهم این دایره می باشد. بنابراین طول این کمان پررنگ شده برابر با یک دوازدهم از محیط این دایره می باشد. محیط دایره (Circumference) با فرمول \(C=2\pi r\) تعیین می شود. این دایره دارای شعاع \(1\) می باشد، بنابراین محیط آن برابر با \(2\pi\) است. از آنجا که این کمان پررنگ شده برابر با یک دوازدهم آن است، طول آن برابر با \(\frac{\pi}{6}\) می باشد، که اندازۀ رادیان این زاویۀ \(30^{\circ}\) است.
\(360^{\circ}\) برابر با \(2\pi\) رادیان است. محیط دایرۀ واحد که \(2\pi\) می باشد، به یاد آوردن اینکه \(360^{\circ}\) برابر با \(2\pi\) رادیان است را ساده کرده است. نصف این محیط دارای طول \(\pi\) است، بنابراین \(180^{\circ}\) درجه برابر با \(\pi\) رادیان است.
اگر بر روی این واقعیت متمرکز شوید که \(180^{\circ}\) درجه برابر با \(\pi\) رادیان است، بدست آوردن معادل رادیان سایر زوایا آسان است:
-
\(90^{\circ}\) برابر با نصف \(180^{\circ}\) درجه است، بنابراین \(90^{\circ}\) درجه برابر با نصف \(\pi\) است، یعنی \(\frac{\pi}{2}\) رادیان.
-
\(60^{\circ}\) برابر با یک سوم \(180^{\circ}\) است، بنابراین \(60^{\circ}\) درجه برابر با یک سوم \(\pi\) است، یعنی \(\frac{\pi}{3}\) .
-
\(45^{\circ}\) برابر با یک چهارم \(180^{\circ}\) است، بنابراین \(45^{\circ}\) برابر با یک چهارم \(\pi\) است، یعنی \(\frac{\pi}{4}\) رادیان.
-
\(30^{\circ}\) برابر با یک ششم \(180^{\circ}\) است، بنابراین \(30^{\circ}\) برابر با یک ششم \(\pi\) است، یعنی \(\frac{\pi}{6}\) رادیان.
فرمول های تبدیل از درجه به رادیان و برعکس:
-
برای تبدیل از درجه به رادیان، اندازۀ آن زاویه را در \(\frac{\pi}{180^{\circ}}\) ضرب کنید.
-
برای تبدیل از رادیان به درجه، اندازۀ آن زاویه را در \(\frac{180^{\circ}}{\pi}\) ضرب کنید.
در ضمن، کلمۀ radian (رادیان) از radius (شعاع) می آید. دوباره به شکل 3-6 بنگرید. زاویه ای با اندازۀ \(1\) رادیان (در حدود \(57^{\circ}\)) کمانی را از دایره جدا می کند که طول آن برابر با شعاع آن دایره است. این مسأله نه تنها درمورد دایرۀ واحد، بلکه در مورد دایره هایی با هر اندازۀ دیگر نیز صدق می کند. به عبارت دیگر، شعاع هر دایره ای را بگیرید، آن را در امتداد محیط دایره قرار دهید، و کمان حاصل از آن برابر با \(1\) رادیان خواهد بود.
رادیان بر درجه ترجیح داده می شود. در این کتاب و هر کتاب حسابان دیگر، برخی از مسأله ها از درجه و برخی دیگر از رادیان استفاده می کنند، اما رادیان واحد ارجح تر است. اگر یک مسأله واحدی را مشخص نکرده باشد، آن مسأله را در واحد رادیان انجام دهید.
تاثیر کوچک یا بزرگ کردن مثلث بر روی مقادیر توابع مثلثاتی
دوباره، به دایرۀ واحد در شکل 3-6 بنگرید. آیا مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) را در ربع صفحۀ اول می بینید؟ این مثلث با مثلثی که در شکل 2-6 (در آموزش قبلی) دیدید هم شکل است اما اندازه اش نصف آن است. هر کدام از این اضلاع نصف آن طول را دارند. از آنجا که وتر آن هم اکنون دارای طول \(1\) می باشد، و از آنجا که وقتیکه \(H\) برابر با \(1\) باشد، \(\frac{O}{H}\) برابر با \(O\) می شود، سینوس این زاویۀ \(30^{\circ}\)، که برابر با \(\frac{O}{H}\) است، برابر با طول ضلع مقابل خواهد بود. ضلع مقابل برابر با \(\frac{1}{2}\) است، بنابراین این سینوس \(30^{\circ}\) است. توجه داشته باشید که طول ضلع روبرو با مختصات \(y\) در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) یکسان است. اگر کسینوس زاویۀ \(30^{\circ}\) را در این مثلث را محاسبه کنید، برابر با طول ضلع مجاور خواهد شد، که با مختصات \(x\) در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) یکسان است. توجه کنید که این مقادیر برای سینوس \(30^{\circ}\) و کسینوس \(30^{\circ}\) با مقادیری که با مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در شکل 2-6 معین شده بودند، یکسان است. این به شما نشان می دهد که کوچک کردن یا بزرگ کردن یک مثلث قائم الزاویه تاثیری بر مقادیر مثلثاتی زوایای آن مثلث ندارد.
اکنون به مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ دوم (quadrant II) در شکل 3-6 بنگرید. از آنجا که این مثلث با مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ اول، که دایره را در نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) قطع کرده بود، هم اندازه است، این مثلث دوم نیز دایره را در نقطه ای که مستقیم روبروی آن قرار دارد و با نقطۀ \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) متقارن است، قطع می کند. مختصات این نقطه در ربع صفحۀ دوم برابر با \(\biggl( -\frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) است. اما یادتان باشد که زوایا در دایرۀ واحد همگی از محور \(x\) مثبت اندازه گیری می شوند، بنابراین وتر این مثلث قائم الزاویه یک زاویۀ \(150^{\circ}\) را می سازد؛ و این زاویه، با نقطۀ \(\biggl( -\frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) مرتبط است. کسینوس \(150^{\circ}\) که با مختصات \(x\) این نقطه تعیین می شود، \(-\frac{\sqrt{3}}{2}\) ، و سینوس \(150^{\circ}\) درجه، برابر با مختصات \(y\)، یعنی \(\frac{1}{2}\) است.
مختصات ها در دایرۀ واحد به شما کسینوس و سینوس یک زاویه را می گویند. ضلع نهایی یک زاویه در دایرۀ واحد، آن دایره را در نقطه ای قطع می کند که مختصات \(x\) آن نقطه برابر با کسینوس آن زاویه و مختصات \(y\) آن نقطه برابر با سینوس آن زاویه می باشد. در اینجا یک یادآور ذهنی داریم: \(x\) و \(y\) در همان ترتیب الفبایی می باشند که cosine و sine هستند.
همۀ اینها را در کنار یکدیگر قرار دهید
به شکل 4-6 بنگرید. حالا که همه چیز را در مورد مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می دانید، به سادگی می توانید بدست آورید که این مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) در ربع صفحۀ اول، دایرۀ واحد را در \(\biggl( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \biggr)\) قطع می کند. و اگر مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در ربع صفحۀ اول را بگیرید که این دایرۀ واحد را در \(-\frac{\sqrt{3}}{2}\) قطع می کند و آن را سروته کنید، به مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) دیگری می رسید که این دایره را در \(\biggl( \frac{1}{2},\frac{\sqrt{3}}{2} \biggr)\) قطع می کند. همانطور که می توانید ببینید، این نقطه همان مختصات زاویۀ \(30^{\circ}\) درجه را به شکل معکوس شده دارد.

چگونه یک مثلث قائم الزاویه را در یک دایرۀ واحد ترسیم کنیم: هرگاه که می خواهید یک مثلث قائم الزاویه را در دایرۀ واحد ترسیم کنید، زاویۀ حاده ای (acute angle) را که برایتان حائز اهمیت است در مبدأ مختصات (origin) ـــ همان \((0,0)\) ـــ قرار دهید و سپس زاویۀ قائمۀ آن را بر روی محور \(x\) قرار دهید ـــ هرگز روی محور \(y\) قرارش ندهید.
\(\frac{\sqrt{3}}{2}\) از \(\frac{1}{2}\) بزرگتر است. برای جلوگیری از اشتباه گرفتن اعداد \(\frac{1}{2}\) و \(\frac{\sqrt{3}}{2}\) در هنگام کار با یک زاویۀ \(30^{\circ}\) یا \(60^{\circ}\) درجه، توجه داشته باشید که از آنجایی که \(\sqrt{3}\) بیشتر از \(1\) است، \(\frac{\sqrt{3}}{2}\) باید بزرگتر از \(\frac{1}{2}\) باشد \(\biggl( \frac{1}{2}=0.5;\frac{\sqrt{3}}{2} \approx 0.87 \biggr)\) . از اینرو، از آنجایی که یک زاویۀ \(30^{\circ}\) دایره را در نقطه ای بیشتر متمایل به سمت راست تا بالا قطع می کند، مختصات \(x\) آن باید از مختصات \(y\) آن بزرگتر باشد. بنابراین، این نقطه باید \(\biggl( \frac{\sqrt{3}}{2},\frac{1}{2} \biggr)\) باشد و نه متضاد آن. این مسأله در مورد زاویۀ \(60^{\circ}\) برعکس است.
حالا به سراغ کلیت ماجرا می رویم. به دلیل تقارن در هر چهار ربع صفحه، این سه نقطه در ربع صفحۀ اول در شکل 4-6 دارای همتایانی در سایر سه ربع صفحۀ دیگر می باشند، که مجموعاً \(12\) نقطۀ شناخته شده را به شما می دهند. چهار نقطۀ قرار گرفته بر روی محورها، یعنی \((1,0)\)، \((0,1)\)، \((-1,0)\)، و \((0,-1)\) را به اینها اضافه کنید، و در مجموع \(16\) نقطه خواهید داشت، که هر کدام از آنها به یک زاویه مرتبط است، شکل 5-6 را ببینید.

این \(16\) جفت از مختصات ها، به صورت اتوماتیک کسینوس و سینوس \(16\) زاویه را به شما می دهند. و از آنجا که \(\tan \theta = \frac{\sin \theta}{\cos \theta}\)، می توانید تانژانت این \(16\) زاویه را با تقسیم مختصات \(y\) یک زاویه بر مختصات \(x\) آن بدست آورید. (توجه داشته باشید، هرگاه که کسینوس یک زاویه برابر با صفر باشد، تانژانت آن تعریف نشده خواهد بود، زیرا شما نمی توانید عددی را بر صفر تقسیم کنید.) در نهایت، می توانید کسکانت، سکانت، و کتانژانت این \(16\) زاویه را نیز بیابید، زیرا این توابع مثلثاتی صرفاً کسرمتقابل سینوس، کسینوس، و تانژانت می باشند. (همان هشدار: هرگاه که سینوس، کسینوس، و تانژانت برابر با صفر باشند، توابع معکوس آنها تعریف نشده خواهند بود.)
دایرۀ واحد را بیاموزید: دانستن مقادیر مثلثاتی از دایرۀ واحد در حسابان کاملاً سودمند است. پس از خودتان امتحان بگیرید. با حفظ کردن مثلث های \(45^{\circ}-45^{\circ}-90^{\circ}\) و \(30^{\circ}-60^{\circ}-90^{\circ}\) آغاز کنید. سپس تجسم کنید که چگونه این مثلث ها در چهار ربع صفحۀ دایرۀ واحد جای می گیرند. از تقارن ربع صفحه ها به عنوان کمک استفاده کنید. با اندکی تمرین، می توانید در محاسبۀ مقادیر این شش تابع مثلثاتی در همۀ این \(16\) زاویه، سریع شوید. (سعی کنید این کار را بدون نگاه کردن به چیزی مانند شکل 5-6 انجام دهید.) و همچنین مشابه این امتحان را با رادیان ها از خودتان بگیرید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: