خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
حل کردن مسأله های حد

هیچکدام از روش های سریعی که در بخش قبلی ارائه کردم برای بیشتر مسأله های حد، جواب نمی دهند. اگر عدد فلش را در عبارت حدی جایگذاری کنید و نتیجه تعریف نشده (undefined) باشد (به استثناء موردی که در بخش قبلی پوشش داده شد)، شما یک مسالۀ حد جدی دارید ـــ و اندکی کار برای انجام دادن. این مهمترین کانون توجه ما در این بخش می باشد. اینها مسأله های حد جالب هستند، مواردیکه احتمالاً دارای حفره های بی نهایت کوچک می باشند، و مواردیکه برای حساب دیفرانسیل (differential calculus) مهم هستند ـــ در فصل 9 موارد بیشتری از آنها را خواهید دید.

هنگامی که عدد فلش را جایگذاری می کنید و نتیجۀ آن تعریف نشده (undefined) باشد (معمولاً بدلیل رسیدن به نتیجۀ \(\frac{0}{0}\))، می توانید چهار چیز را امتحان کنید: ماشین حسابتان، جبر، ایجاد یک ساندویچ حد، و قاعدۀ هوپیتال (L’Hôpital’s rule) ـــ در مورد این قاعده در فصل 18 بحث شده است.
فرض کنید می خواهید حد زیر را ارزیابی کنید:
$$\lim \limits_{x \to 5} \frac{x^2-25}{x-5}$$
روش جایگذاری و حل (plug-and-chug) جواب نمی دهد، زیرا جایگذاری \(5\) در \(x\) منجر به تولید نتیجۀ تعریف نشدۀ \(\frac{0}{0}\) می شود، اما همانند بیشتر مسأله های حد، می توانید این مسأله را با ماشین حسابتان حل کنید.
ماشین حسابی همچون TI-Nspire (یا هر ماشین حساب دیگری که مجهز به سیستم کامپیوتری جبر ـــ \(\text{CAS: Computer Algebra System}\) ـــ باشد) می تواند این مسالۀ حد (و همۀ انواع دیگر مسأله های پیچیده تر حسابان) را حل کند و پاسخ دقیق را به شما بدهد. همچنین وبسایتهایی همچون Wolfram Alpha می توانند این کار را برای شما انجام دهند.
معلم های حسابان مختلف، در مورد اینکه چه فناوری هایی را در کلاسشان اجازه دهند، سیاست های مختلفی دارند. بسیاری از دبیران اجازۀ استفاده از فناوری هایی که از CAS و فناوری های نظیر آن را استفاده می کنند، نمی دهند، زیرا آنها عملاً همۀ کار حسابان را برای شما انجام می دهند. بنابراین، بحثی که در ادامه آمده است (و بقیۀ این کتاب) فرض می گیرد که شما از یک ماشین حساب سادۀ پایه ای تر همچون مدل TI-84 استفاده می کنید که به قابلیت CAS مجهز نمی باشد.
اولین روش ماشین حساب اینست که تابع حد را با دو عدد امتحان کنید: یکی اندکی کمتر از عدد فلش، و دیگری اندکی بیشتر از آن. در اینجا آنچه که برای مسالۀ بالا، \(\lim \limits_{x \to 5} \frac{x^2-25}{x-5}\) ، انجام می دهید را می بینید. اگر ماشین حسابی همچون مدل TI-84 دارید، اولین عدد را وارد کنید، فرض کنید \(4.9999\) باشد، سپس دکمۀ Sto که مخفف store (ذخیره کردن) هست را بفشارید، سپس دکمۀ \(x\)، و سپس دکمۀ Enter را بفشارید (این کار منجر می شود تا آن عدد در \(x\) ذخیره گردد). سپس تابع \(\frac{x^2-25}{x-5}\) را وارد کنید و Enter کنید. نتیجه، \(9.9999\) ، به شدت به عدد گرد شدۀ \(10\) نزدیک می باشد، بنابراین احتمالاً \(10\) پاسخ شما باشد. اکنون عددی اندکی بیشتر از عدد فلش را در نظر بگیرید، مانند \(5.0001\) ، و این فرآیند را تکرار کنید. از آنجا که این نتیجه برابر با \(10.0001\) است، آن نیز به \(10\) خیلی نزدیک است، این پاسخ اول را اثبات می کند. این پاسخ \(10\) است (تقریباً به طور قطع). راستی، اگر از ماشین حسابی با مدل دیگری استفاده می کنید، می توانید با همین تکنیک، یا چیزی نزدیک به آن، به نتیجۀ یکسانی برسید.
دومین روش ماشین حساب اینست که جدولی از مقادیر ایجاد کنید. \(y=\frac{x^2-25}{x-5}\) را در حالت نموداری ماشین حسابتان وارد کنید. سپس به "table set up" (تنظیم جدول) بروید و عدد فلش، \(5\) ، را به عنوان عدد "table start" (آغاز کنندۀ جدول) وارد کنید، و یک عدد کوچک، فرضاً \(0.001\)، برای \(\triangle{} \text{Tbl} \) وارد کنید ـــ این اندازۀ افزایش \(x\) در جدول می باشد. دکمۀ Table (جدول) را فشار دهید تا این جدول ایجاد گردد. اکنون بالا بروید تا اینکه بتوانید چندین عدد کمتر از \(5\) را ببینید، و باید جدولی از مقادیر مشابه جدول 1-8 را ببینید.
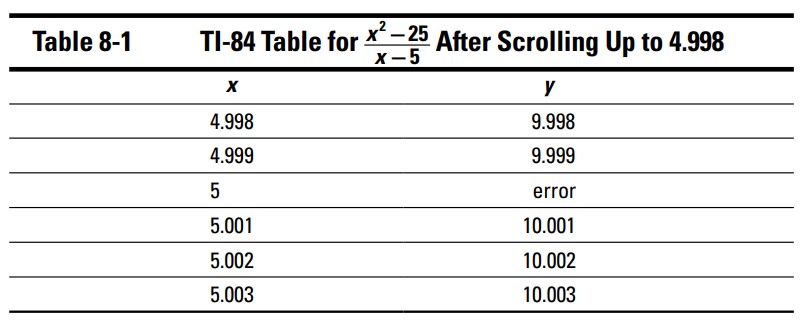
از آنجا که، همینطور که \(x\) از بالا و پایین به \(5\) نزدیک می گردد، \(y\) به \(10\) بسیار نزدیک می شود، \(10\) برابر با حد است (تقریباً به طور قطع ... شما نمی توانید با این روش ماشین حساب کاملاً مطمئن باشید، اما آنها تقریباً همیشه جواب می دهند).
این روش های ماشین حساب به برخی دلایل سودمند هستند. ماشین حساب شما پاسخ مسأله های حدی را که به شکل جبری رسیدن به آنها غیرممکن می باشد، می دهد. و می تواند مسأله های حدی را برای شما حل کند که هرچند حل کردن آنها با کاغذ و قلم شدنی است اما بسیار گیج کننده و مشکلند. همچنین، مسأله هایی را که بر روی کاغذ حل کرده اید، می توانید با ماشین حساب درست آزمایی نمایید. و حتی هنگامی که انتخاب شما حل کردن یک حد به صورت جبری می باشد ـــ یا مجبور به انجام این کار هستید ـــ فکر خوبی است که جدولی مشابه جدول 1-8 بسازید، نه صرفاً به منظور تایید پاسختان، بلکه برای مشاهدۀ اینکه آن تابع در نزدیک عدد فلش چگونه رفتار می کند. این کار یک فهم عددی در آن مسأله به شما می دهد، که درک جبری شما از آن را تقویت می کند. اگر بعد از آن به نمودار آن تابع در ماشین حسابتان بنگرید، شما یک روش سومی برای تفکر بصری یا گرافیکی در مورد آن مسأله دارید.
از روش ماشین حساب برای تکمیل روش جبری استفاده کنید، اما زیاد متکی به آنها نشوید. قبل از هر چیز، ماشین حساب هایی که از ویژگی CAS برخوردار نباشند، به شما اجازه نمی دهند تا یک پاسخ دقیق را نتیجه گیری کنید، مگر اینکه اعدادی که ماشین حسابتان به شما می دهد به عددی که قبلاً می شناسید نزدیک باشد ـــ مانند \(9.999\) که به \(10\) نزدیک است، یا \(0.333332\) که به \(\frac{1}{3}\) نزدیک است؛ یا شاید شما متوجه شوید که \(1.414211\) به \(\sqrt{2}\) بسیار نزدیک است. اما اگر پاسخ آن مسالۀ حد، چیزی شبیه \(\frac{1}{2\sqrt{3}}\) باشد، شما احتمالاً قادر به شناسایی آن نباشید. عدد \(\frac{1}{2\sqrt{3}}\) تقریباً برابر با \(0.288675\) است. هنگامی که اعدادی را در جدولتان می بینید که به آن عدد اعشاری نزدیک می شوند، \(\frac{1}{2\sqrt{3}}\) را به عنوان آن حد شناسایی نخواهید کرد ـــ مگر اینکه شما یک ارشمیدس (Archimedes)، یک گاوس (Gauss)، یا یک رامانوجان (Ramanujan) باشید. (این سه نفر ریاضیدانانی هستند که در تالار مشاهیر ریاضی قرار دارند). با این حال، حتی موقعی که نتوانید پاسخ دقیق (exact answer) را در چنین مواردی شناسایی کنید، هنوز هم می توانید یک پاسخ تقریبی را در شکل اعشاری، برای آن سوال حد بدست آورید.
در ضمن، حتی در مواقعی که ماشین حسابهای غیر مجهز به CAS می توانند از عهدۀ مسأله برآیند، این ماشین حسابها گاه به گاه در ارتباط با مسأله ها دمدمی مزاج برخورد می کنند. به عنوان مثال، اگر مشغول حل کردن یک مسالۀ حد باشید که در آن \(x\) به \(3\) نزدیک می شود، و اعدادی را در ماشین حسابتان قرار دهید که بسیار به \(3\) نزدیک باشند (مانند \(3.0000000001\))، ممکن است به حداکثر طول قابل پشتیبانی در آن ماشین حساب نزدیک شوید. این می تواند منجر به نتیجه ای شود که بیشتر از پاسخ آن حد است، حتی با وجود اینکه اعدادی را که به عدد فلش نزدیک و نزدیکتر شده اند را وارد نموده اید.
نتیجۀ اخلاقی این داستان اینست که شما باید به ماشین حسابتان به عنوان یکی از چندین ابزاری که برای حل کردن حدها در اختیار دارید بنگرید ـــ و نه به عنوان جایگزینی برای تکنیک های جبری.
شما دو روش جبری اصلی را برای حل کردن مسأله های واقعی حد، استفاده می کنید: فاکتورگیری (factoring)، و ضرب در مزدوج (conjugate multiplication). در ادامه روش های جبری دیگری را نیز مطرح خواهم نمود. تمامی روش های جبری شامل مفاهیم اصلی یکسانی هستند. هنگامی که جایگذاری در تابع اصلی جواب نمی دهد ـــ معمولاً بدلیل وجود یک حفره در آن تابع ـــ شما می توانید از جبر برای دستکاری آن تابع استفاده کنید تا زمانی که جایگذاری جواب بدهد (این روش به این دلیل جواب می دهد که دستکاری شما آن حفره را پر می کند).
در اینجا مثالی داریم. \(\lim \limits_{x \to 5} \frac{x^2-25}{x-5}\) را ارزیابی کنید، همان مسأله ای که در بخش قبلی با ماشین حساب حلش کردید:
در ضمن، تابعی که بعد از خط زدن \((x-5)\) بدست آوردید، یعنی \(y=(x+5)\)، با تابع اصلی، \(y= \frac{x^2-25}{x-5}\)، یکی است، با این استثناء که حفرۀ موجود در \((5,10)\)، در تابع اصلی، پُر شده است. و توجه داشته باشید که این حد همچنان که \(x\) به \(5\) نزدیک می شود، برابر با \(10\) است، که برابر با ارتفاع این حفره در \((5,10)\) می باشد.
این روش را برای توابع کسری شامل جذرها مورد استفاده قرار دهید. ضرب مزدوج، صورت یا مخرج یک کسر را گویا (rationalizes) می کند، گویا کردن به معنای رهایی یافتن از جذرها می باشد. این مورد را امتحان کنید:
$$\lim \limits_{x \to 4} \frac{\sqrt{x}-2}{x-4}$$
همانند مثال فاکتورگیری، این فرآیند گویا سازی نیز، حفرۀ موجود در تابع اصلی را می پوشاند. در این مثال، \(4\) عدد فلش (arrow-number)، و \(\frac{1}{4}\) پاسخ این حد، و تابع \(\frac{\sqrt{x}-2}{x-4}\) دارای حفره ای در \((4,\frac{1}{4})\) می باشد.
هنگامی که فاکتورگیری و ضرب در مزدوج درست جواب نمی دهد، سایر جبرهای پایه ای را امتحان کنید، مانند جمع یا تفریق کسرها، ضرب یا تقسیم کسرها، خط زدن، یا سایر شکل های ساده سازی. در اینجا مثالی داریم:
$$\lim \limits_{x \to 0} \frac{\frac{1}{x+4}-\frac{1}{4}}{x} $$
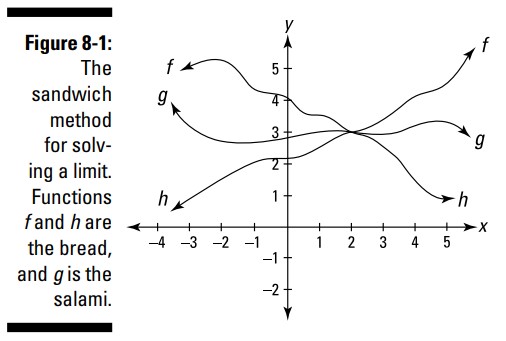
هنگامی که جبر جواب نمی دهد، سعی کنید یک ساندویچ حد درست کنید. بهترین روش برای درک ساندویچ یا روش فشردن (squeeze) اینست که به یک نمودار نگاه کنید. شکل 1-8 را ببینید.
به توابع \(f\)، \(g\)، و \(h\) در شکل 1-8 بنگرید: \(g\) بین \(f\) و \(h\) ساندویچ شده است. از آنجایی که نزدیک عدد فلش \(2\)، \(f\) همیشه بالاتر یا هم ارتفاع با \(g\) می باشد، و \(g\) همیشه بالاتر یا هم ارتفاع با \(h\) می باشد، و از آنجاییکه \(\lim \limits_{x \to 2} f(x) = \lim \limits_{x \to 2} h(x)\)، سپس \(g(x)\) همانطور که \(x\) به \(2\) نزدیک می شود، باید دارای حد یکسانی باشد، زیرا بین \(f\) و \(h\) ساندویچ یا فشرده شده است. حد هر دو تابع \(f\) و \(h\)، همینطور که \(x\) به \(2\) میل می کند، برابر با \(3\) می باشد. بنابراین، \(3\) باید حد \(g\) نیز باشد. هیچ جای دیگری برای رفتن ندارد.
در اینجا مثال دیگری داریم، حد زیر را ارزیابی کنید:
$$\lim \limits_{x \to 0} \biggl( x \sin \frac{1}{x} \biggr)$$

هنگامی که عدد فلش را جایگذاری می کنید و نتیجۀ آن تعریف نشده (undefined) باشد (معمولاً بدلیل رسیدن به نتیجۀ \(\frac{0}{0}\))، می توانید چهار چیز را امتحان کنید: ماشین حسابتان، جبر، ایجاد یک ساندویچ حد، و قاعدۀ هوپیتال (L’Hôpital’s rule) ـــ در مورد این قاعده در فصل 18 بحث شده است.
محاسبۀ یک حد با ماشین حسابتان
فرض کنید می خواهید حد زیر را ارزیابی کنید:
$$\lim \limits_{x \to 5} \frac{x^2-25}{x-5}$$
روش جایگذاری و حل (plug-and-chug) جواب نمی دهد، زیرا جایگذاری \(5\) در \(x\) منجر به تولید نتیجۀ تعریف نشدۀ \(\frac{0}{0}\) می شود، اما همانند بیشتر مسأله های حد، می توانید این مسأله را با ماشین حسابتان حل کنید.
به ماشین حسابها و سایر فناوری ها توجه کنید. هر سال که می گذرد، ماشین حسابهای قدرتمندتری بوجود می آیند، و منابع بیشتر و بیشتری بر روی اینترنت بوجود می آیند که می توانند حسابان را برای شما انجام دهند. این فناوری ها می توانند به عنوان مثال پاسخ \(5x^3-4x\)، در حالی که این مسأله نیازمند یک پاسخ جبری می باشد را به شما بدهند، یا به عنوان مثال، پاسخ \(\sqrt{2}\) (نه فقط تخمین \(1.414\)) را در حالی که این مسأله نیازمند یک پاسخ عددی است، به شما بدهند. ماشین حسابهای قدیمی تر نمی توانستند به شما یک پاسخ جبری بدهند، و با وجود اینکه آنها می توانستند پاسخ های دقیق بسیاری از مسأله های عددی را به شما بدهند، نمی توانستند یک پاسخ دقیق عددی همچون \(\sqrt{2}\) را به شما بدهند ـــ و همچنین آنها نمی توانستند یک پاسخ دقیق به مسالۀ حد موجود در پاراگراف قبلی را به شما بدهند.
ماشین حسابی همچون TI-Nspire (یا هر ماشین حساب دیگری که مجهز به سیستم کامپیوتری جبر ـــ \(\text{CAS: Computer Algebra System}\) ـــ باشد) می تواند این مسالۀ حد (و همۀ انواع دیگر مسأله های پیچیده تر حسابان) را حل کند و پاسخ دقیق را به شما بدهد. همچنین وبسایتهایی همچون Wolfram Alpha می توانند این کار را برای شما انجام دهند.
معلم های حسابان مختلف، در مورد اینکه چه فناوری هایی را در کلاسشان اجازه دهند، سیاست های مختلفی دارند. بسیاری از دبیران اجازۀ استفاده از فناوری هایی که از CAS و فناوری های نظیر آن را استفاده می کنند، نمی دهند، زیرا آنها عملاً همۀ کار حسابان را برای شما انجام می دهند. بنابراین، بحثی که در ادامه آمده است (و بقیۀ این کتاب) فرض می گیرد که شما از یک ماشین حساب سادۀ پایه ای تر همچون مدل TI-84 استفاده می کنید که به قابلیت CAS مجهز نمی باشد.
روش 1
اولین روش ماشین حساب اینست که تابع حد را با دو عدد امتحان کنید: یکی اندکی کمتر از عدد فلش، و دیگری اندکی بیشتر از آن. در اینجا آنچه که برای مسالۀ بالا، \(\lim \limits_{x \to 5} \frac{x^2-25}{x-5}\) ، انجام می دهید را می بینید. اگر ماشین حسابی همچون مدل TI-84 دارید، اولین عدد را وارد کنید، فرض کنید \(4.9999\) باشد، سپس دکمۀ Sto که مخفف store (ذخیره کردن) هست را بفشارید، سپس دکمۀ \(x\)، و سپس دکمۀ Enter را بفشارید (این کار منجر می شود تا آن عدد در \(x\) ذخیره گردد). سپس تابع \(\frac{x^2-25}{x-5}\) را وارد کنید و Enter کنید. نتیجه، \(9.9999\) ، به شدت به عدد گرد شدۀ \(10\) نزدیک می باشد، بنابراین احتمالاً \(10\) پاسخ شما باشد. اکنون عددی اندکی بیشتر از عدد فلش را در نظر بگیرید، مانند \(5.0001\) ، و این فرآیند را تکرار کنید. از آنجا که این نتیجه برابر با \(10.0001\) است، آن نیز به \(10\) خیلی نزدیک است، این پاسخ اول را اثبات می کند. این پاسخ \(10\) است (تقریباً به طور قطع). راستی، اگر از ماشین حسابی با مدل دیگری استفاده می کنید، می توانید با همین تکنیک، یا چیزی نزدیک به آن، به نتیجۀ یکسانی برسید.
روش 2
دومین روش ماشین حساب اینست که جدولی از مقادیر ایجاد کنید. \(y=\frac{x^2-25}{x-5}\) را در حالت نموداری ماشین حسابتان وارد کنید. سپس به "table set up" (تنظیم جدول) بروید و عدد فلش، \(5\) ، را به عنوان عدد "table start" (آغاز کنندۀ جدول) وارد کنید، و یک عدد کوچک، فرضاً \(0.001\)، برای \(\triangle{} \text{Tbl} \) وارد کنید ـــ این اندازۀ افزایش \(x\) در جدول می باشد. دکمۀ Table (جدول) را فشار دهید تا این جدول ایجاد گردد. اکنون بالا بروید تا اینکه بتوانید چندین عدد کمتر از \(5\) را ببینید، و باید جدولی از مقادیر مشابه جدول 1-8 را ببینید.

از آنجا که، همینطور که \(x\) از بالا و پایین به \(5\) نزدیک می گردد، \(y\) به \(10\) بسیار نزدیک می شود، \(10\) برابر با حد است (تقریباً به طور قطع ... شما نمی توانید با این روش ماشین حساب کاملاً مطمئن باشید، اما آنها تقریباً همیشه جواب می دهند).
این روش های ماشین حساب به برخی دلایل سودمند هستند. ماشین حساب شما پاسخ مسأله های حدی را که به شکل جبری رسیدن به آنها غیرممکن می باشد، می دهد. و می تواند مسأله های حدی را برای شما حل کند که هرچند حل کردن آنها با کاغذ و قلم شدنی است اما بسیار گیج کننده و مشکلند. همچنین، مسأله هایی را که بر روی کاغذ حل کرده اید، می توانید با ماشین حساب درست آزمایی نمایید. و حتی هنگامی که انتخاب شما حل کردن یک حد به صورت جبری می باشد ـــ یا مجبور به انجام این کار هستید ـــ فکر خوبی است که جدولی مشابه جدول 1-8 بسازید، نه صرفاً به منظور تایید پاسختان، بلکه برای مشاهدۀ اینکه آن تابع در نزدیک عدد فلش چگونه رفتار می کند. این کار یک فهم عددی در آن مسأله به شما می دهد، که درک جبری شما از آن را تقویت می کند. اگر بعد از آن به نمودار آن تابع در ماشین حسابتان بنگرید، شما یک روش سومی برای تفکر بصری یا گرافیکی در مورد آن مسأله دارید.
بسیاری از مسأله های حسابان می توانند به صورت جبری (algebraically)، گرافیکی (graphically)، و عددی (numerically) حل شوند. هرگاه که شدنی باشد، از دو یا سه تا از این رویکردها استفاده کنید. هر رویکرد، چشم انداز متفاوتی از آن مسأله را به شما می دهد و درک شما از مفاهیم مرتبط را تقویت می کند.
از روش ماشین حساب برای تکمیل روش جبری استفاده کنید، اما زیاد متکی به آنها نشوید. قبل از هر چیز، ماشین حساب هایی که از ویژگی CAS برخوردار نباشند، به شما اجازه نمی دهند تا یک پاسخ دقیق را نتیجه گیری کنید، مگر اینکه اعدادی که ماشین حسابتان به شما می دهد به عددی که قبلاً می شناسید نزدیک باشد ـــ مانند \(9.999\) که به \(10\) نزدیک است، یا \(0.333332\) که به \(\frac{1}{3}\) نزدیک است؛ یا شاید شما متوجه شوید که \(1.414211\) به \(\sqrt{2}\) بسیار نزدیک است. اما اگر پاسخ آن مسالۀ حد، چیزی شبیه \(\frac{1}{2\sqrt{3}}\) باشد، شما احتمالاً قادر به شناسایی آن نباشید. عدد \(\frac{1}{2\sqrt{3}}\) تقریباً برابر با \(0.288675\) است. هنگامی که اعدادی را در جدولتان می بینید که به آن عدد اعشاری نزدیک می شوند، \(\frac{1}{2\sqrt{3}}\) را به عنوان آن حد شناسایی نخواهید کرد ـــ مگر اینکه شما یک ارشمیدس (Archimedes)، یک گاوس (Gauss)، یا یک رامانوجان (Ramanujan) باشید. (این سه نفر ریاضیدانانی هستند که در تالار مشاهیر ریاضی قرار دارند). با این حال، حتی موقعی که نتوانید پاسخ دقیق (exact answer) را در چنین مواردی شناسایی کنید، هنوز هم می توانید یک پاسخ تقریبی را در شکل اعشاری، برای آن سوال حد بدست آورید.
توابع مشکل ممکن است ماشین حساب شما را از پا در آورند. دومین محدودیت ماشین حسابها اینست که به هیچ وجه نمی توانند برخی از توابع عجیب و غریب مانند \(\lim \limits_{x \to 5} \sqrt[25]{x-5} \cdot \sin\biggl( \frac{1}{x-5} \biggr)\) را محاسبه کنند. این حد برابر با صفر می باشد، اما نمی توانید با ماشین حسابتان این نتیجه را بدست آورید.
در ضمن، حتی در مواقعی که ماشین حسابهای غیر مجهز به CAS می توانند از عهدۀ مسأله برآیند، این ماشین حسابها گاه به گاه در ارتباط با مسأله ها دمدمی مزاج برخورد می کنند. به عنوان مثال، اگر مشغول حل کردن یک مسالۀ حد باشید که در آن \(x\) به \(3\) نزدیک می شود، و اعدادی را در ماشین حسابتان قرار دهید که بسیار به \(3\) نزدیک باشند (مانند \(3.0000000001\))، ممکن است به حداکثر طول قابل پشتیبانی در آن ماشین حساب نزدیک شوید. این می تواند منجر به نتیجه ای شود که بیشتر از پاسخ آن حد است، حتی با وجود اینکه اعدادی را که به عدد فلش نزدیک و نزدیکتر شده اند را وارد نموده اید.
نتیجۀ اخلاقی این داستان اینست که شما باید به ماشین حسابتان به عنوان یکی از چندین ابزاری که برای حل کردن حدها در اختیار دارید بنگرید ـــ و نه به عنوان جایگزینی برای تکنیک های جبری.
حل کردن مسأله های حد با جبر
شما دو روش جبری اصلی را برای حل کردن مسأله های واقعی حد، استفاده می کنید: فاکتورگیری (factoring)، و ضرب در مزدوج (conjugate multiplication). در ادامه روش های جبری دیگری را نیز مطرح خواهم نمود. تمامی روش های جبری شامل مفاهیم اصلی یکسانی هستند. هنگامی که جایگذاری در تابع اصلی جواب نمی دهد ـــ معمولاً بدلیل وجود یک حفره در آن تابع ـــ شما می توانید از جبر برای دستکاری آن تابع استفاده کنید تا زمانی که جایگذاری جواب بدهد (این روش به این دلیل جواب می دهد که دستکاری شما آن حفره را پر می کند).
فاکتورگیری (factoring)
در اینجا مثالی داریم. \(\lim \limits_{x \to 5} \frac{x^2-25}{x-5}\) را ارزیابی کنید، همان مسأله ای که در بخش قبلی با ماشین حساب حلش کردید:
-
سعی کنید \(5\) را در \(x\) جایگذاری کنید ـــ شما همیشه باید قبل از هر چیز جایگذاری را امتحان کنید.
به نتیجۀ \(\frac{0}{0}\) می رسید ـــ خوب نیست، به سراغ پلن \(B\) می رویم.
-
\(x^2-25\) می تواند فاکتورگیری شود، بنابراین این کار را انجام دهید.
$$\lim \limits_{x \to 5} \frac{x^2-25}{x-5}=\lim \limits_{x \to 5} \frac{(x-5)(x+5)}{x-5}$$
-
\((x-5)\) را از صورت و مخرج این کسر خط بزنید.
$$=\lim \limits_{x \to 5} (x+5)$$
-
اکنون جایگذاری جواب می دهد.
$$=5+5=10$$
در ضمن، تابعی که بعد از خط زدن \((x-5)\) بدست آوردید، یعنی \(y=(x+5)\)، با تابع اصلی، \(y= \frac{x^2-25}{x-5}\)، یکی است، با این استثناء که حفرۀ موجود در \((5,10)\)، در تابع اصلی، پُر شده است. و توجه داشته باشید که این حد همچنان که \(x\) به \(5\) نزدیک می شود، برابر با \(10\) است، که برابر با ارتفاع این حفره در \((5,10)\) می باشد.
ضرب در مزدوج (Conjugate multiplication)
این روش را برای توابع کسری شامل جذرها مورد استفاده قرار دهید. ضرب مزدوج، صورت یا مخرج یک کسر را گویا (rationalizes) می کند، گویا کردن به معنای رهایی یافتن از جذرها می باشد. این مورد را امتحان کنید:
$$\lim \limits_{x \to 4} \frac{\sqrt{x}-2}{x-4}$$
-
جایگذاری را امتحان کنید.
\(4\) را جایگذاری کنید: نتیجه بدست آمده \(\frac{0}{0}\) می باشد ـــ نوبت به پلن \(B\) می رسد.
-
صورت و مخرج را در مزدوج \(\sqrt{x}-2\)، که برابر با \(\sqrt{x}+2\) می باشد، ضرب کنید.
تعریف مزدوج (conjugate): مزدوج یک عبارت دو جمله ای، صرفاً همان عبارت است که در آن تفریق به جمع، و یا جمع به تفریق تغییر یافته است. حاصلضرب مزدوج ها همواره برابر با مربع جملۀ اول منهای مربع جملۀ دوم می باشد.
اکنون گویا سازی (rationalizing) را انجام می دهیم.
$$\lim \limits_{x \to 4} \frac{\sqrt{x}-2}{x-4} \\
=\lim \limits_{x \to 4} \frac{(\sqrt{x}-2)}{x-4} \cdot \frac{(\sqrt{x}+2)}{(\sqrt{x}+2)} \\
=\lim \limits_{x \to 4} \frac{(\sqrt{x})^2 -2^2}{(x-4)(\sqrt{x}+2)} \\
=\lim \limits_{x \to 4} \frac{(x-4)}{(x-4)(\sqrt{x}+2)} $$
-
\((x-4)\) را از صورت و مخرج این کسر خط بزنید.
$$=\lim \limits_{x \to 4} \frac{1}{\sqrt{x}+2} $$
-
اکنون روش جایگذاری جواب می دهد.
$$=\frac{1}{\sqrt{4}+2}=\frac{1}{4}$$
همانند مثال فاکتورگیری، این فرآیند گویا سازی نیز، حفرۀ موجود در تابع اصلی را می پوشاند. در این مثال، \(4\) عدد فلش (arrow-number)، و \(\frac{1}{4}\) پاسخ این حد، و تابع \(\frac{\sqrt{x}-2}{x-4}\) دارای حفره ای در \((4,\frac{1}{4})\) می باشد.
روش های جبری متفرقه
هنگامی که فاکتورگیری و ضرب در مزدوج درست جواب نمی دهد، سایر جبرهای پایه ای را امتحان کنید، مانند جمع یا تفریق کسرها، ضرب یا تقسیم کسرها، خط زدن، یا سایر شکل های ساده سازی. در اینجا مثالی داریم:
$$\lim \limits_{x \to 0} \frac{\frac{1}{x+4}-\frac{1}{4}}{x} $$
-
جایگذاری را امتحان کنید.
جایگذاری \(0\) نتیجۀ \(\frac{0}{0}\) را به شما می دهد ـــ خوب نیست.
-
این کسر مرکب (complex fraction) را با ضرب کردن صورت و مخرج آن در کوچکترین مخرج مشترکِ کسرهای کوچکتر، ینی \(4(x+4)\) ساده کنید (کسر مرکب یک کسر بزرگ است که شامل کسرهایی باشد).
توجه: شما همچنین می توانید یک کسر مرکب را با جمع یا تفریق کردن کسرهای کوچکتر در صورت و مخرج یا در هر دوی اینها، ساده کنید، اما روشی که در اینجا توصیف شده است، اندکی سریعتر است.
$$\lim \limits_{x \to 0} \frac{\frac{1}{x+4}-\frac{1}{4}}{x} \\
= \lim \limits_{x \to 0} \frac{\biggl( \frac{1}{x+4}-\frac{1}{4} \biggr)}{x} \cdot \frac{4(x+4)}{4(x+4)} \\
= \lim \limits_{x \to 0} \frac{4-(x+4)}{4x(x+4)} \\
= \lim \limits_{x \to 0} \frac{-x}{4x(x+4)} \\
= \lim \limits_{x \to 0} \frac{-1}{4(x+4)}
$$
-
اکنون روش جایگذاری جواب می دهد.
$$=\frac{-1}{4(0+4)}= - \frac{1}{16}$$
ساندویچ حد (limit sandwich)
هنگامی که جبر جواب نمی دهد، سعی کنید یک ساندویچ حد درست کنید. بهترین روش برای درک ساندویچ یا روش فشردن (squeeze) اینست که به یک نمودار نگاه کنید. شکل 1-8 را ببینید.
به توابع \(f\)، \(g\)، و \(h\) در شکل 1-8 بنگرید: \(g\) بین \(f\) و \(h\) ساندویچ شده است. از آنجایی که نزدیک عدد فلش \(2\)، \(f\) همیشه بالاتر یا هم ارتفاع با \(g\) می باشد، و \(g\) همیشه بالاتر یا هم ارتفاع با \(h\) می باشد، و از آنجاییکه \(\lim \limits_{x \to 2} f(x) = \lim \limits_{x \to 2} h(x)\)، سپس \(g(x)\) همانطور که \(x\) به \(2\) نزدیک می شود، باید دارای حد یکسانی باشد، زیرا بین \(f\) و \(h\) ساندویچ یا فشرده شده است. حد هر دو تابع \(f\) و \(h\)، همینطور که \(x\) به \(2\) میل می کند، برابر با \(3\) می باشد. بنابراین، \(3\) باید حد \(g\) نیز باشد. هیچ جای دیگری برای رفتن ندارد.

در اینجا مثال دیگری داریم، حد زیر را ارزیابی کنید:
$$\lim \limits_{x \to 0} \biggl( x \sin \frac{1}{x} \biggr)$$
-
جایگذاری را امتحان کنید.
\(0\) را در \(x\) جایگذاری کنید. نتیجۀ \(0 \cdot \frac{1}{0}\) را به شما می دهد ـــ خوب نیست، تقسیم بر صفر میسر نیست. به سراغ پلن \(B\) می رویم.
-
روش های جبری یا هر ترفند دیگری را که در آستین دارید، امتحان کنید.
خودتان را نکشید. نمی توانید آن را انجام بدهید. به سراغ پلن \(C\) می رویم.
-
ماشین حسابتان را امتحان کنید.
همیشه فکر خوبی ست که ببنید ماشین حسابتان به شما چه می گوید، حتی اگر مسالۀ شما از نوعی باشد که راه حل مرحله به مرحله اش را هم از شما خواسته باشند. برای ترسیم نموداری این تابع، ماشین حساب نموداری تان را بر روی حالت radian (رادیان) تنظیم کنید و window (پنجره) آن را اینگونه تنظیم کنید:
$$
x \min = -0.4 \\
x \max = 0.4 \\
y \min = -0.3 \\
y \max = 0.3
$$
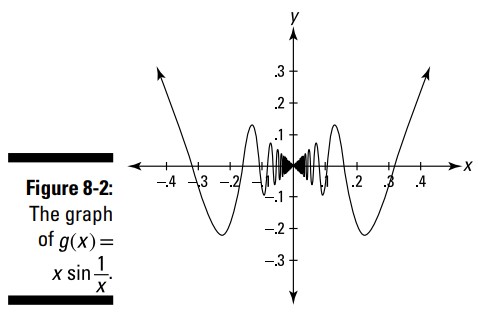
شکل 2-8 این نمودار را به شما نشان می دهد.
قطعاً به نظر می رسد، حد \(g\)، همینطور که \(x\) از سمت چپ و راست به صفر نزدیک می شود، برابر با صفر باشد. اکنون، جدول مقادیر را در ماشین حسابتان بررسی کنید (TblStart را برابر با \(0\) و \(\triangle{} \text{Tbl}\) را برابر با \(0.001\) قرار دهید). جدول 2-8 برخی از مقادیر این جدول در ماشین حساب را نشان می دهد.
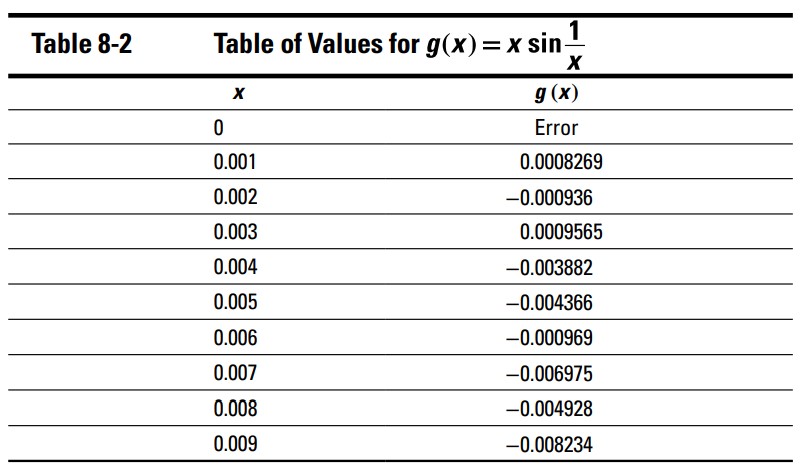
هینطور که \(x\) به صفر نزدیک می شود، این اعداد به نوعی به نظر می رسد که به صفر نزدیک و نزدیکتر می شوند، اما متقاعد کننده نیستند. این نوع از جدول برای توابع نوسانی (oscillating functions) مانند سینوس و کسینوس، خیلی خوب کار نمی کند. (برخی از مقادیر تابع در جدول، به عنوان مثال \(-0.000969\) برای \(x=0.006\)، نسبت به مقادیر دیگری بزرگتر از آن در حالیکه \(x\) شان در جدول کوچکتر است، به صفر نزدیکتر است. این متضاد چیزی است که ما می خواهیم ببینیم.)
یک روش بهتر برای مشاهدۀ اینکه، همینطور که \(x\) به صفر میل می کند، این حد از \(g\) برابر با صفر است، استفاده از روش اول ماشین حساب است که در همین آموزش در موردش بحث کردیم. این تابع را در صفحۀ اصلی ماشین حساب وارد کنید و متعاقب آن مقادیری را که در جدول 3-8 لیست شده اند، در \(x\) جایگذاری کنید تا مقادیر متناظر توابع را بدست آورید. (توجه: یک چیزی را اشتباه نگیرید: جدول 3-8 ، جدول نامیده می شود، اما جدولی نیست که توسط تابع جدول در یک ماشین حساب تولید شده باشد.)
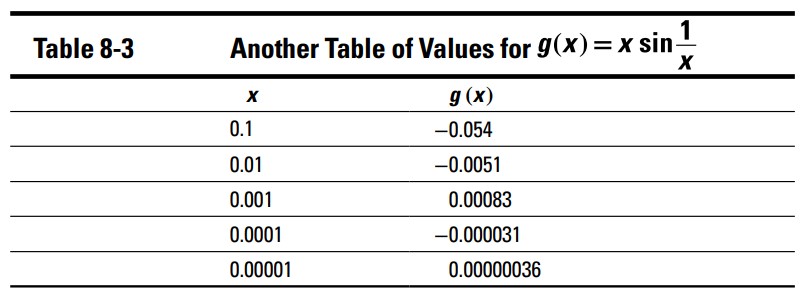
اکنون می توانید یقیناً ببینید که \(g\) به سمت صفر می رود.
-
اکنون نیاز دارید تا این حد را به صورت ریاضی اثبات کنید، حتی با وجود اینکه هم اکنون آن را در ماشین حسابتان حل کرده اید. برای انجام این کار، یک ساندویچ حد بسازید.
سختترین قسمت استفاده از روش ساندویچ، رسیدن به توابع نانها می باشد. (توابع \(f\) و \(h\) نان هستند، و تابع \(g\) سوسیس این ساندویچ می باشد.) هیچ روش اتوماتیکی برای انجام این کار وجود ندارد. شما باید به شکل این تابع سوسیس فکر کنید، و سپس از دانشتان در مورد توابع استفاده کنید و همینطور از قدرت خیال پردازیتان استفاده کنید تا به یک چشم انداز خوب از توابع نان برسید.
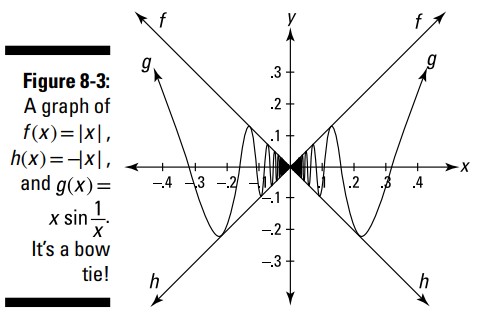
از آنجا که بُرد (range) تابع سینوس از منفی \(1\) تا مثبت \(1\) می باشد، هرگاه که عددی را در سینوس چیزی ضرب کنید، نتیجۀ آن یا از صفر دارای همان فاصله خواهد بود و یا اینکه به صفر نزدیک تر می شود. از اینرو، \(x \sin \frac{1}{x}\) هرگز از \(|x|\) بالاتر نخواهد رفت یا از \(-|x|\) پایینتر نخواهد آمد. بنابراین سعی کنید نمودار توابع \(f(x)=|x|\) و \(h(x)=-|x|\) را همراه با \(g(x)\) ترسیم کنید تا ببینید آیا \(f\) و \(h\) توابع نان مناسبی برای \(g\) هستند. شکل 3-8 نشان می دهد که اینطور است. ما نشان داده ایم که \(f(x) \ge g(x) \ge h(x)\) . و از آنجا که \(\lim \limits_{x \to 0} f(x) = \lim \limits_{x \to 0} h(x)\)، به دنبال آن \(g(x)\) باید حد یکسانی داشته باشد: \(\lim \limits_{x \to 0} g(x) = 0\) .
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: