خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ارزیابی حدها در بی نهایت

در بخش های پیشین، حدهایی را بررسی کردم که در آنها \(x\) به یک عدد متناهی (finite number) نزدیک می شد، اما شما همچنین می توانید حدهایی داشته باشید که در آنها \(x\) به بی نهایت (infinity) یا منفی بی نهایت (negative infinity) میل می کند. تابع \(f(x)=\frac{1}{x}\) را در نظر بگیرید و نمودار آن را در شکل 4-8 بررسی کنید.

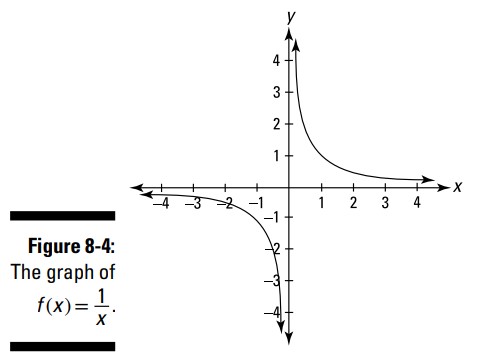
شما در این نمودار می توانید ببینید که (در ربع صفحۀ اول) همینطور که \(x\) بزرگ و بزرگتر می شود ـــ به عبارت دیگر، همینطور که \(x\) به بی نهایت نزدیک می شود ـــ ارتفاع این تابع کوچک و کوچکتر می شود اما هرگز به صفر نمی رسد. با ملاحظۀ اینکه وقتیکه اعداد بزرگ و بزرگتری را در \(\frac{1}{x}\) جایگذاری می کنید، چه رخ می دهد، این مطلب تایید می شود: خروجی ها کوچک و کوچکتر می گردند و به صفر نزدیک می شوند. بدین ترتیب این نمودار دارای یک خط مجانب افقی \(y=0\) (محور \(x\)) می باشد، و ما می گوییم که \(\lim \limits_{x \to \infty} \frac{1}{x} = 0\) . این حقیقت که \(x\) واقعاً هرگز به بی نهایت نمی رسد و \(f\) هرگز به صفر نمی رسد، ارتباطی با یکدیگر ندارند. هنگامی که می گوییم \(\lim \limits_{x \to \infty} \frac{1}{x} = 0\) ، همینطور که \(x\) بزرگ و بزرگتر می شود، بدون اینکه خاتمه یابد، \(f\) به ارتفاع صفر نزدیک می شود (یا \(f\) در نهایت بی نهایت به ارتفاع صفر نزدیک می شود). اگر به ربع صفحۀ سوم بنگرید، می توانید ببینید که تابع \(f\)، همینطور که \(x\) به منفی بی نهایت میل می کند، به صفر نیز نزدیک می شود، که به شکل \(\lim \limits_{x \to -\infty} \frac{1}{x} = 0\) نوشته می شود.
حدها در بی نهایت و خطهای مجانب افقی با یکدیگر ارتباط تنگاتنگی دارند. تعیین اینکه حد یک تابع همچنانکه \(x\) به بی نهایت یا منفی بی نهایت نزدیک می شود، با یافتن ارتفاع خط مجانب افقی یکسان است.
بیایید با بررسی توابع گویا (rational functions) کار را آغاز کنیم. در اینجا چگونگی یافتن حد در بی نهایت و منفی بی نهایت (و ارتفاع خط مجانب افقی) از یک تابع گویا (چیزی شبیه \(f(x)=\frac{3x-7}{2x+8}\)) را می بینید. ابتدا، به درجۀ صورت کسر (این درجه بالاترین توان \(x\) در صورت کسر می باشد) و درجۀ مخرج کسر توجه کنید. آنها سه حالت دارند:
در اینجا مسأله ای داریم که نمی تواند با روش ارائه شده در بخش قبلی حل شود زیرا یک تابع گویا نمی باشد:
$$\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr)$$
اما این مسأله با ماشین حساب به سادگی یک بشکن زدن حل می شود. این تابع را در حالت نموداری (graphing mode) وارد کنید، سپس به تنظیمات جدول (table setup) بروید و TblStart را به \(100,000\) و \(\triangle{} \text{Tbl}\) را به \(100,000\) تنظیم کنید. جدول 4-8 نتایج را به شما نشان می دهد.
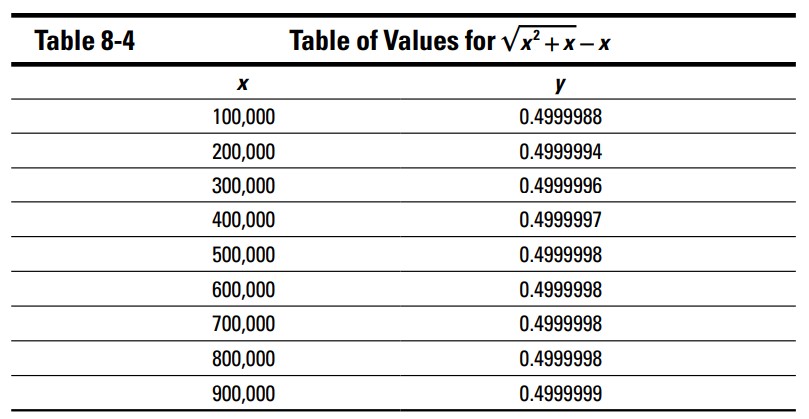
شما می توانید ببینید که همینطور که \(x\) بزرگ و بزرگتر می شود، \(y\) به شدت به \(0.5\) نزدیک می شود. بنابراین \(0.5\) حد این تابع، همینطور که \(x\) به بی نهایت نزدیک می شود، می باشد، و یک خط مجانب افقی در \(y=0.5\) وجود دارد. اگر در اینکه این حد برابر با \(0.5\) است، شک دارید، به تنظیمات جدول (table setup) باز گردید و یک مقدار بسیار بزرگ مانند \(1,000,000,000\) را برای TblStart و \(\triangle{} \text{Tbl}\) وارد کنید، و نتایج جدول را دوباره بررسی کنید. تمام چیزی که می بینید ستونی از \(0.5\) ها خواهد بود. این حد است. (در ضمن، برخلاف توابع گویا در دو بخش پیشین، حد این تابع همچنانکه \(x\) به منفی بی نهایت نزدیک می شود با حد آن زمانیکه \(x\) به مثبت بی نهایت نزدیک می شود، یکی نیست:
$$\lim \limits_{x \to -\infty} \biggl( \sqrt{x^2+x}-x \biggr) = \infty$$
زیرا هنگامی که \(-\infty\) را در آن جایگذاری می کنید به \(\infty+\infty\) می رسید که برابر با \(\infty\) است. یک چیز دیگر: درست مانند حدهای معمولی، استفاده از یک ماشین حساب بدون قابلیت سیستم جبر کامپیوتری (CAS: Computer Algebra System) برای حدهای بی نهایت، پاسخ دقیقی را به شما نمی دهد، مگر اینکه اعداد موجود در جدول به عددی که می شناسید، مانند \(0.5\) نزدیک باشد.
اکنون قدری جبر را برای مسالۀ \(\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr)\) امتحان کنید. شما با ماشین حساب به پاسخ رسیده اید، اما اگر همه چیز همانطور که باید پیش برود، پاسخها یکسان خواهند بود، بهتر اینست که این مسأله را به صورت جبری نیز حل کنید، زیرا در آنصورت یک پاسخ محکم ریاضی خواهید داشت. پاسخ ماشین حساب به این مورد بسیار متقاعد کننده است، اما به لحاظ ریاضی خیلی دقیق نیست، بنابراین، اگر در همینجا متوقف شوید، پلیس ریاضی شما را دستگیر خواهد کرد!


شما در این نمودار می توانید ببینید که (در ربع صفحۀ اول) همینطور که \(x\) بزرگ و بزرگتر می شود ـــ به عبارت دیگر، همینطور که \(x\) به بی نهایت نزدیک می شود ـــ ارتفاع این تابع کوچک و کوچکتر می شود اما هرگز به صفر نمی رسد. با ملاحظۀ اینکه وقتیکه اعداد بزرگ و بزرگتری را در \(\frac{1}{x}\) جایگذاری می کنید، چه رخ می دهد، این مطلب تایید می شود: خروجی ها کوچک و کوچکتر می گردند و به صفر نزدیک می شوند. بدین ترتیب این نمودار دارای یک خط مجانب افقی \(y=0\) (محور \(x\)) می باشد، و ما می گوییم که \(\lim \limits_{x \to \infty} \frac{1}{x} = 0\) . این حقیقت که \(x\) واقعاً هرگز به بی نهایت نمی رسد و \(f\) هرگز به صفر نمی رسد، ارتباطی با یکدیگر ندارند. هنگامی که می گوییم \(\lim \limits_{x \to \infty} \frac{1}{x} = 0\) ، همینطور که \(x\) بزرگ و بزرگتر می شود، بدون اینکه خاتمه یابد، \(f\) به ارتفاع صفر نزدیک می شود (یا \(f\) در نهایت بی نهایت به ارتفاع صفر نزدیک می شود). اگر به ربع صفحۀ سوم بنگرید، می توانید ببینید که تابع \(f\)، همینطور که \(x\) به منفی بی نهایت میل می کند، به صفر نیز نزدیک می شود، که به شکل \(\lim \limits_{x \to -\infty} \frac{1}{x} = 0\) نوشته می شود.
حدها در بی نهایت و خط های مجانب افقی
حدها در بی نهایت و خطهای مجانب افقی با یکدیگر ارتباط تنگاتنگی دارند. تعیین اینکه حد یک تابع همچنانکه \(x\) به بی نهایت یا منفی بی نهایت نزدیک می شود، با یافتن ارتفاع خط مجانب افقی یکسان است.
بیایید با بررسی توابع گویا (rational functions) کار را آغاز کنیم. در اینجا چگونگی یافتن حد در بی نهایت و منفی بی نهایت (و ارتفاع خط مجانب افقی) از یک تابع گویا (چیزی شبیه \(f(x)=\frac{3x-7}{2x+8}\)) را می بینید. ابتدا، به درجۀ صورت کسر (این درجه بالاترین توان \(x\) در صورت کسر می باشد) و درجۀ مخرج کسر توجه کنید. آنها سه حالت دارند:
-
اگر درجۀ صورت کسر از درجۀ مخرج آن بزرگتر باشد، به عنوان مثال \(f(x)=\frac{6x^4+x^3-7}{2x^2+8}\)، هیچ خط مجانب افقی وجود نخواهد داشت، و حد این تابع، همچنانکه \(x\) به بی نهایت (یا منفی بی نهایت) میل می کند، وجود نخواهد داشت (این حد برابر با مثبت بی نهایت یا منفی بی نهایت خواهد بود).
-
اگر درجۀ مخرج کسر بزرگتر از درجۀ صورت آن باشد، به عنوان مثال \(g(x)=\frac{4x^2-9}{x^3+12}\)، محور \(x\) (خط \(y=0\)) خط مجانب افقی خواهد بود، و \(\lim \limits_{x \to \infty} g(x)=\lim \limits_{x \to -\infty} g(x) = 0\) .
-
اگر درجۀ صورت کسر و مخرج کسر برابر باشند، ضریب بالاترین توان \(x\) در صورت کسر را بگیرید و آن را بر ضریب بالاترین توان \(x\) در مخرج کسر، تقسیم کنید. این خارج قسمت، پاسخ این مسالۀ حد و ارتفاع خط مجانب را به شما می دهد. به عنوان مثال، اگر \(h(x)=\frac{4x^3-10x+1}{5x^3+2x^2-x}\)، خواهیم داشت، \(\lim \limits_{x \to \infty} h(x) = \lim \limits_{x \to -\infty} h(x) = \frac{4}{5}\) ، و \(h\) یک خط مجانب افقی در \(y=\frac{4}{5}\) خواهد داشت.
همانند یک پروفسور صحبت کنید. برای اینکه دوستانتان را تحت تاثیر قرار دهید، انگشت نشانۀ تان را رو به سمت بالا کنید، یکی از ابروهایتان را بالا ببرید، و با یک تن صدای پروفسوری بگویید، "در یک تابع گویا که صورت و مخرج آن دارای درجۀ برابر باشند، حد تابع همچنان که \(x\) به بی نهایت یا منفی بی نهایت میل می کند، برابر با خارج قسمت ضریب های جملات پیش رو (leading terms) می باشد. یک خط مجانب افقی در مقدار یکسانی با آن رخ می دهد."
\(\frac{\infty}{\infty}\) برابر با \(1\) نمی باشد. جایگذاری برای مسأله های این بخش جواب نمی دهد. اگر در هر کدام از توابع گویا در این بخش، \(\infty\) را در \(x\) جایگذاری کنید، به \(\frac{\infty}{\infty}\) می رسید، اما این الزاماً برابر با \(1\) نمی باشد (گاهی اوقات \(\frac{\infty}{\infty}\) برابر با \(1\) است، اما اغلب اینطور نیست). یک نتیجۀ \(\frac{\infty}{\infty}\) هیچ چیزی در مورد پاسخ یک مسالۀ حد، به شما نمی گوید.
حل کردن حدها در بی نهایت با ماشین حساب
در اینجا مسأله ای داریم که نمی تواند با روش ارائه شده در بخش قبلی حل شود زیرا یک تابع گویا نمی باشد:
$$\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr)$$
اما این مسأله با ماشین حساب به سادگی یک بشکن زدن حل می شود. این تابع را در حالت نموداری (graphing mode) وارد کنید، سپس به تنظیمات جدول (table setup) بروید و TblStart را به \(100,000\) و \(\triangle{} \text{Tbl}\) را به \(100,000\) تنظیم کنید. جدول 4-8 نتایج را به شما نشان می دهد.

شما می توانید ببینید که همینطور که \(x\) بزرگ و بزرگتر می شود، \(y\) به شدت به \(0.5\) نزدیک می شود. بنابراین \(0.5\) حد این تابع، همینطور که \(x\) به بی نهایت نزدیک می شود، می باشد، و یک خط مجانب افقی در \(y=0.5\) وجود دارد. اگر در اینکه این حد برابر با \(0.5\) است، شک دارید، به تنظیمات جدول (table setup) باز گردید و یک مقدار بسیار بزرگ مانند \(1,000,000,000\) را برای TblStart و \(\triangle{} \text{Tbl}\) وارد کنید، و نتایج جدول را دوباره بررسی کنید. تمام چیزی که می بینید ستونی از \(0.5\) ها خواهد بود. این حد است. (در ضمن، برخلاف توابع گویا در دو بخش پیشین، حد این تابع همچنانکه \(x\) به منفی بی نهایت نزدیک می شود با حد آن زمانیکه \(x\) به مثبت بی نهایت نزدیک می شود، یکی نیست:
$$\lim \limits_{x \to -\infty} \biggl( \sqrt{x^2+x}-x \biggr) = \infty$$
زیرا هنگامی که \(-\infty\) را در آن جایگذاری می کنید به \(\infty+\infty\) می رسید که برابر با \(\infty\) است. یک چیز دیگر: درست مانند حدهای معمولی، استفاده از یک ماشین حساب بدون قابلیت سیستم جبر کامپیوتری (CAS: Computer Algebra System) برای حدهای بی نهایت، پاسخ دقیقی را به شما نمی دهد، مگر اینکه اعداد موجود در جدول به عددی که می شناسید، مانند \(0.5\) نزدیک باشد.
\(\infty - \infty\) برابر با صفر نمی باشد. جایگذاری در مورد مسالۀ بالا، \(\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr)\) ، درست جواب نمی دهد. اگر \(\infty\) را در \(x\) جایگذاری کنید، به \(\infty - \infty\) می رسید، که الزاماً برابر با صفر نمی باشد (\(\infty - \infty\) گاهی اوقات برابر با صفر می شود، اما اغلب اینگونه نیست). یک نتیجۀ \(\infty - \infty\) در مورد پاسخ یک مسالۀ حد، هیچ چیزی را به شما نمی گوید.
حل کردن حدها در بی نهایت با جبر
اکنون قدری جبر را برای مسالۀ \(\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr)\) امتحان کنید. شما با ماشین حساب به پاسخ رسیده اید، اما اگر همه چیز همانطور که باید پیش برود، پاسخها یکسان خواهند بود، بهتر اینست که این مسأله را به صورت جبری نیز حل کنید، زیرا در آنصورت یک پاسخ محکم ریاضی خواهید داشت. پاسخ ماشین حساب به این مورد بسیار متقاعد کننده است، اما به لحاظ ریاضی خیلی دقیق نیست، بنابراین، اگر در همینجا متوقف شوید، پلیس ریاضی شما را دستگیر خواهد کرد!
-
جایگذاری را بیازمایید ـــ همیشه فکر خوبی است.
نتیجه خوب نیست. به \(\infty - \infty\) می رسید، که هیچ چیزی را به شما نمی گوید ـــ هشدار موجود در بخش قبلی را ببینید. به سراغ پلن \(B\) می رویم.
از آنجا که \(\biggl( \sqrt{x^2+x}-x \biggr)\) شامل یک جذر است، روش ضرب مزدوج می تواند یک انتخاب طبیعی باشد، به استثناء اینکه این روش برای توابع کسری مورد استفاده قرار می گیرد. خوب، کافیست \(\biggl( \sqrt{x^2+x}-x \biggr)\) را بر روی عدد \(1\) قرار دهید، خوب شد، شما به یک کسر می رسید: \(\frac{\biggl( \sqrt{x^2+x}-x \biggr)}{1}\) . اکنون ضرب مزدوج (conjugate multiplication) را انجام دهید.
-
صورت و مخرج این کسر را در مزدوج \(\biggl( \sqrt{x^2+x}-x \biggr)\) ضرب کرده و ساده سازی کنید.
$$
\lim \limits_{x \to \infty} \frac{\biggl( \sqrt{x^2+x}-x \biggr)}{1} \\
=\lim \limits_{x \to \infty} \frac{\biggl( \sqrt{x^2+x}-x \biggr)}{1} \cdot \frac{\biggl( \sqrt{x^2+x}+x \biggr)}{\biggl( \sqrt{x^2+x}+x \biggr)} \\
=\lim \limits_{x \to \infty} \frac{x^2+x-x^2}{\sqrt{x^2+x}+x}$$
(ابتدا \(x^2\) را در صورت کسر خط بزنید. سپس \(x\) را از مخرج کسر فاکتور بگیرید. بله، درست شنیده اید.)
$$\lim \limits_{x \to \infty} \frac{x}{x\biggl( \sqrt{1+\frac{1}{x}}+1 \biggr)}$$
(اکنون \(x\) ها را خط بزنید.)
$$\lim \limits_{x \to \infty} \frac{1}{\sqrt{1+\frac{1}{x}}+1}$$
-
حالا روش جایگذاری درست جواب خواهد داد.
$$= \frac{1}{\sqrt{1+\frac{1}{\infty}}+1} $$
(از بخش حدهای ساده که پیشتر در همین فصل تاکید کردیم حفظشان کنید، به خاطر بیاورید که \(\lim \limits_{x \to \infty} \frac{1}{x} = 0\))
$$
= \frac{1}{\sqrt{1+0}+1} \\
= \frac{1}{1+1}=\frac{1}{2} \\
$$
بدین ترتیب، \(\lim \limits_{x \to \infty} \biggl( \sqrt{x^2+x}-x \biggr) = \frac{1}{2}\) ، که پاسخ بدست آمده در ماشین حساب را تصدیق می کند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: