خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
یافتن اکسترمم های موضعی

اکنون که بخش قبلی را فرا گرفته اید و تجربه کرده اید، و می دانید که اکسترمم های موضعی (local extrema) چه هستند، نیاز دارید تا عملیات ریاضی برای یافتن آنها را بدانید. شما در بخش پیشین دیدید که تمامی اکسترمم های موضعی در نقاط بحرانی (critical points) یک تابع رخ می دهند ـــ در نقطۀ بحرانی مشتق تابع برابر با صفر یا تعریف نشده می باشد ـــ اما فراموش نکنید که نقاط بحرانی همیشه اکسترمم موضعی نمی باشند. بنابراین، اولین گام در یافتن اکسترمم های موضعی یک تابع اینست که اعداد بحرانی (critical numbers) آن را بیابید ـــ اعداد بحرانی عبارت از مقادیر \(x\) در نقاط بحرانی می باشند.

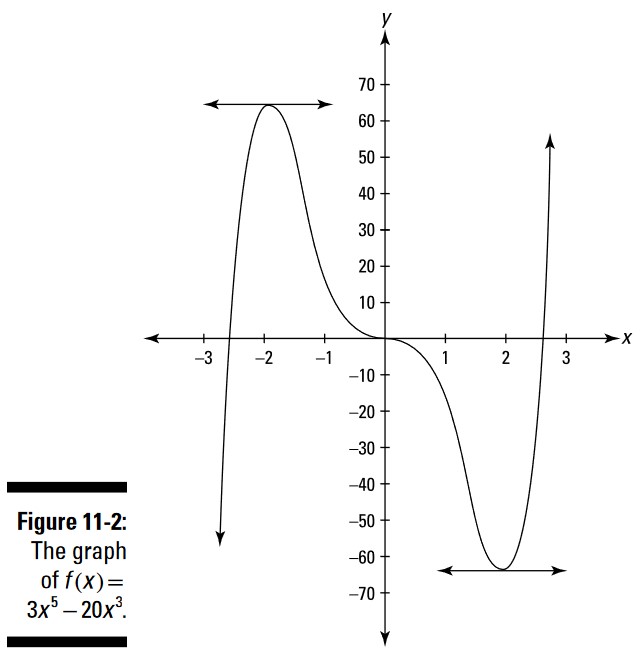
اعداد بحرانی \(f(x)=3x^5-20x^3\) را بیابید. شکل 2-11 را ببینید.
این چیزی است که باید انجام دهید:
حالا که شما لیست اعدد بحرانی را بدست آورده اید، نیاز دارید تا تعیین کنید که آیا در آن مقادیر \(x\)، قله ها یا دره ها یا نقاط عطف رخ داده اند یا خیر. شما می توانید این را با آزمون مشتق اول یا آزمون مشتق دوم، انجام دهید. من فرض می کنم شما با خودتان اندیشیده اید چرا باید این اعداد حیاتی را آزمایش کنید، در حالیکه می توانید صرفاً با نگاه کردن به نمودار در شکل 2-11 ـــ که مسلماً می توانید آن را با ماشین حساب نموداریتان نیز تولید کنید ـــ ببینید این قله ها و دره ها کجا هستند. نکتۀ خوبی بود. اوکی، این مسأله قدری ساختگی و غیرعملی است. لازم نیست اشاره کنم که تعداد بیشمار دیگری از مسأله های ریاضی که در دوره های ریاضی انجام می دهید نیز همینطورند. خوب دیگه چی؟
آزمون مشتق اول مبتنی بر این مفهوم است که وقتیکه شما می خواهید به نوک تپه ای بروید و برگردید، ابتدا بالا می روید و سپس پایین می آیید، و هنگامی که به داخل یک دره وارد می شوید و سپس از آن خارج می گردید، ابتدا پایین می روید و سپس بالا می آیید.
در اینجا چگونگی انجام این آزمون را می بینید. یک خط اعداد را در نظر بگیرید و اعداد حیاتی را که یافته اید بر روی آن قرار دهید: \(0\)، \(-2\)، و \(2\). شکل 3-11 را ببینید.
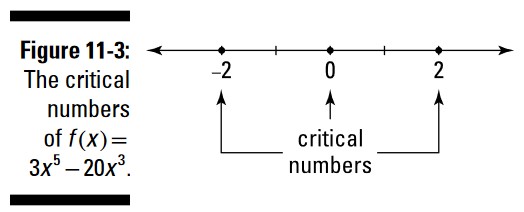
این خط اعداد (number line) اکنون به چهار ناحیه تقسیم شده است: سمت چپ \(-2\)، از \(-2\) تا \(0\)، از \(0\) تا \(2\)، و سمت راست \(2\). عددی را از هر ناحیه انتخاب کنید، آن را در مشتق اول جایگذاری کنید، و توجه کنید که آیا نتیجۀ بدست آمده مثبت است یا منفی. بیایید از اعداد \(-3\)، \(-1\)، \(1\)، و \(3\) برای آزمایش این ناحیه ها استفاده کنیم:
$$
f'(x)=15x^4-60x^2 \\
f'(-3)=15(-3)^4-60(-3)^2=15 \cdot 81 - 60 \cdot 9=675 \\
f'(-1)=15(-1)^4-60(-1)^2=15 - 60 =-45 \\
f'(1)=15(1)^4-60(1)^2=15 - 60 =-45 \\
f'(3)=15(3)^4-60(3)^2=15 \cdot 81 - 60 \cdot 9=675
$$
در ضمن، اگر متوجه شدید که اولین مشتق یک تابع زوج (even function) می باشد، بدون انجام این محاسبات، باید بدانید که، \(f(1)=f(-1)\) و \(f(3)=f(-3)\). (در فصل 5 توابع زوج مورد بحث قرار گرفتند. یک تابع چندجمله ای که تمامی توان های آن زوج باشد، مانند \(f'(x)\) در بالا، که یکی از انواع توابع زوج می باشد.)
این چهار نتیجۀ بدست آمده، به ترتیب؛ مثبت، منفی، منفی، و مثبت می باشند. اکنون به سراغ خط اعدادتان بروید، هر ناحیه از آن را با علامت مثبت یا منفی مناسب مشخص سازید، و نشان دهید که این تابع در کجاها افزایش می یابد (جایی که مشتق در آن مثبت باشد) و در کجاها کاهش می یابد (جایی که مشتق در آن منفی باشد). این نتیجه به اصطلاح نمودار علامت (sign graph) نامیده می شود. شکل 4-11 را ببینید. (چهار فلش رو به سمت راست در بالای این شکل به سادگی نشان می دهند که این "در حال افزایش" و "در حال کاهش" به شما می گویند همینطور که از چپ به راست می روید چه اتفاقی می افتد.)
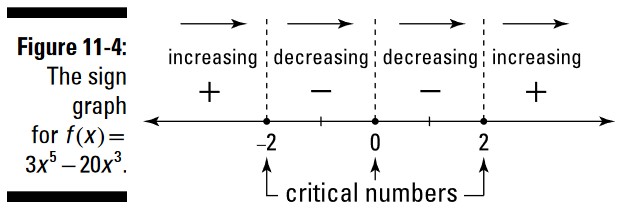
شکل 4-11 به سادگی به شما می گوید اگر به نمودار \(f\) بنگرید چه چیزی را از روی آن خواهید دانست ـــ اینکه این تابع تا \(-2\) بالا می رود، از \(-2\) تا \(0\) پایین می رود، از \(0\) تا \(2\) پایینتر می رود، و دوباره از \(2\) بالا می رود.
این تابع در \(-2\) از درحال افزایش به در حال کاهش، تغییر می کند؛ به عبارت دیگر، شما تا \(-2\) بالا می روید و بعد از آن پایین می آیید. بنابراین در \(-2\) بالای یک تپه یا یک ماکزیمم موضعی دارید. برعکس، از آنجا که این تابع در \(2\) از در حال کاهش به در حال افزایش تغییر می کند، شما در آنجا ته یک دره یا یک مینیمم موضعی دارید. و از آنجا که علامت اولین مشتق در صفر تغییر نمی کند (از مثبت به منفی یا برعکس)، در این مقدار \(x\) نه یک مینیمم و نه یک ماکزیمم وجود دارد (وقتی این اتفاق می افتد، ـــ مانند همینجا ـــ شما معمولاً یک نقطۀ عطف افقی بدست می آورید).
آخرین مرحله اینست که با جایگذاری مقادیر \(x\) در تابع اصلی، مقادیر توابع، به عبارت دیگر ارتفاع ها، را برای این دو اکسترمم موضعی بدست آورید:
$$
f(x)=3x^5-20x^3 \\
f(-2)=3(-2)^5-20(-2)^3=64 \\
f(2)=3(2)^5-20(2)^3=-64
$$
بدین ترتیب، ماکزیمم موضعی در \((-2,64)\) و مینیمم موضعی در \((2,-64)\) قرار گرفته است. کار تمام است.
آزمون مشتق دوم مبتنی بر دو مفهوم است: ابتدا اینکه در قلۀ یک تپه، یک جاده به شکل کوهان شتر (hump shape) می باشد ـــ به عبارت دیگر رو به سمت پایین خم می شود یا تقعر رو به پایین دارد؛ و دوم اینکه، در انتهای یک دره، یک جاده به شکل فنجان (cup-shaped) می باشد، بنابراین رو به سمت بالا خم می شود یا تقعر رو به بالا دارد.
تقعر یک تابع در یک نقطه با مشتق دوم آن بدست می آید: یک مشتق دوم مثبت بدین معناست که آن تابع در آنجا تقعر رو به بالا دارد، یک مشتق دوم منفی بدین معناست که آن تابع تقعر رو به پایین دارد، و یک مشتق دوم صفر بی نتیجه می باشد (این تابع می تواند تقعر رو به سمت بالا یا تقعر رو به سمت پایین داشته باشد، یا می تواند در آنجا یک نقطۀ عطف وجود داشته باشد). بنابراین، در تابع ما، \(f\)، تمام کاری که شما باید انجام دهید اینست که مشتق دوم آن را بیابید و سپس اعداد بحرانی پیدا شده را در آنها جایگذاری کنید، \(-2\)، \(0\)، و \(2\)، و توجه کنید که آیا نتایج شما مثبت، منفی، یا صفر می باشند. بعبارت دیگر:
$$
f(x)=3x^5-20x^3 \\
f'(x)=15x^4-60x^2 \\
f''(x)=60x^3-120x \\
f''(-2)=60(-2)^3-120(-2)=-240\\
f''(0)=60(0)^3-120(0)=0\\
f''(2)=60(2)^3-120(2)=240
$$
در \(x=-2\)، مشتق دوم، \((-240)\)، منفی می باشد. این به شما می گوید که \(f\) در جاییکه \(x\) برابر با \(-2\) می باشد، تقعر رو به پایین دارد، و بدین ترتیب در آنجا یک ماکزیمم نسبی وجود دارد. مشتق دوم، \((240)\)، در جاییکه \(x\) برابر با \(2\) است، مثبت می باشد، بنابراین \(f\) در آنجا تقعر رو به بالا دارد و بدین ترتیب یک مینیمم نسبی در \(x=2\) وجود دارد. از آنجا که مشتق دوم در \(x=0\) برابر با صفر می باشد، آزمون مشتق دوم برای این عدد بحرانی با شکست مواجه می شود ـــ این عدد صفر هیچ چیزی را در مورد تقعر در \(x=0\) یا اینکه آیا در آنجا یک ماکزیمم یا مینیمم نسبی وجود دارد یا خیر، به شما نمی گوید. وقتیکه این اتفاق می افتد، شما باید از آزمون مشتق اول استفاده کنید.
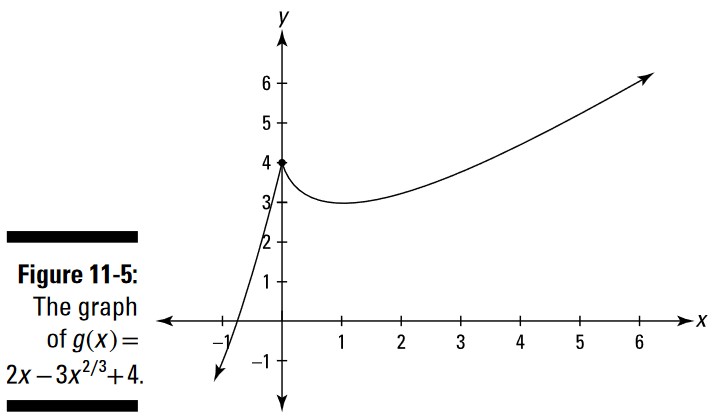
حالا در مثالی دیگر، یکبار دیگر وارد مراحل آزمون مشتق اول و دوم می شویم. اکسترمم های موضعی \(g(x)=2x-3x^{\frac{2}{3}} +4\) را بیابید. شکل 5-11 را ببینید.
شما می توانید از آزمون مشتق دوم به جای آزمون مشتق اول در مرحلۀ 4 استفاده کنید. در ابتدا، به مشتق دوم \(g\) نیاز دارید، که همانطور که خودتان هم می دانید، برابر با مشتقِ مشتق اول آن می باشد:
$$
g'(x)=2-2x^{-\frac{1}{3}} \\
g''(x)=\frac{2}{3}x^{-\frac{4}{3}}
$$
مشتق دوم را در \(x=1\) ارزیابی کنید (این یک عدد بحرانی از مرحلۀ 2 می باشد):
$$g''(1)=\frac{2}{3}$$
از آنجا که \(g''(1)\) مثبت می باشد، شما می دانید که \(g\) در \(x=1\) تقعر رو به بالا دارد و ، بدین ترتیب، یک مینیمم نسبی در آنجا وجود دارد.
در عدد بحرانی دیگر، \(x=0\) (از مرحلۀ 3)، اولین مشتق تعریف نشده است. جایی که مشتق اول تعریف نشده باشد، آزمون مشتق دوم کمکی نخواهد کرد، شما باید از آزمون مشتق اول برای این عدد بحرانی استفاده کنید.

تولید انبوه اعداد بحرانی
اعداد بحرانی \(f(x)=3x^5-20x^3\) را بیابید. شکل 2-11 را ببینید.
این چیزی است که باید انجام دهید:
-
اولین مشتق \(f\) را با استفاده از قانون توان (power rule) بیابید.
$$f(x)=3x^5 - 20x^3 \\
f'(x)=15x^4-60x^2$$
-
این مشتق را برابر با صفر قرار دهید و آن را برای بدست آوردن \(x\) حل کنید.
$$
15x^4-60x^2=0 \\
15x^2(x^2-4)=0 \\
15x^2(x+2)(x-2)=0 \\
15x^2 = 0 \text{ or } x+2=0 \text{ or } x-2=0 \\
x=0 \text{ or } x=-2 \text{ or } x=2
$$
یک منحنی هرجا که مشتق آن برابر با صفر باشد، یعنی در نقاط سکون آن (stationary points)، یک خط تانژانت افقی دارد. یک منحنی در تمامی مینیمم ها و ماکزیمم های وضعی اش (به استثناء گوشه های تیز مانند \(j\) در شکل 1-11) و در تمامی نقاط عطف افقی اش، دارای خطهای تانژانت افقی خواهد بود.
حالا که شما لیست اعدد بحرانی را بدست آورده اید، نیاز دارید تا تعیین کنید که آیا در آن مقادیر \(x\)، قله ها یا دره ها یا نقاط عطف رخ داده اند یا خیر. شما می توانید این را با آزمون مشتق اول یا آزمون مشتق دوم، انجام دهید. من فرض می کنم شما با خودتان اندیشیده اید چرا باید این اعداد حیاتی را آزمایش کنید، در حالیکه می توانید صرفاً با نگاه کردن به نمودار در شکل 2-11 ـــ که مسلماً می توانید آن را با ماشین حساب نموداریتان نیز تولید کنید ـــ ببینید این قله ها و دره ها کجا هستند. نکتۀ خوبی بود. اوکی، این مسأله قدری ساختگی و غیرعملی است. لازم نیست اشاره کنم که تعداد بیشمار دیگری از مسأله های ریاضی که در دوره های ریاضی انجام می دهید نیز همینطورند. خوب دیگه چی؟
آزمون مشتق اول (first derivative test)
آزمون مشتق اول مبتنی بر این مفهوم است که وقتیکه شما می خواهید به نوک تپه ای بروید و برگردید، ابتدا بالا می روید و سپس پایین می آیید، و هنگامی که به داخل یک دره وارد می شوید و سپس از آن خارج می گردید، ابتدا پایین می روید و سپس بالا می آیید.
در اینجا چگونگی انجام این آزمون را می بینید. یک خط اعداد را در نظر بگیرید و اعداد حیاتی را که یافته اید بر روی آن قرار دهید: \(0\)، \(-2\)، و \(2\). شکل 3-11 را ببینید.

این خط اعداد (number line) اکنون به چهار ناحیه تقسیم شده است: سمت چپ \(-2\)، از \(-2\) تا \(0\)، از \(0\) تا \(2\)، و سمت راست \(2\). عددی را از هر ناحیه انتخاب کنید، آن را در مشتق اول جایگذاری کنید، و توجه کنید که آیا نتیجۀ بدست آمده مثبت است یا منفی. بیایید از اعداد \(-3\)، \(-1\)، \(1\)، و \(3\) برای آزمایش این ناحیه ها استفاده کنیم:
$$
f'(x)=15x^4-60x^2 \\
f'(-3)=15(-3)^4-60(-3)^2=15 \cdot 81 - 60 \cdot 9=675 \\
f'(-1)=15(-1)^4-60(-1)^2=15 - 60 =-45 \\
f'(1)=15(1)^4-60(1)^2=15 - 60 =-45 \\
f'(3)=15(3)^4-60(3)^2=15 \cdot 81 - 60 \cdot 9=675
$$
در ضمن، اگر متوجه شدید که اولین مشتق یک تابع زوج (even function) می باشد، بدون انجام این محاسبات، باید بدانید که، \(f(1)=f(-1)\) و \(f(3)=f(-3)\). (در فصل 5 توابع زوج مورد بحث قرار گرفتند. یک تابع چندجمله ای که تمامی توان های آن زوج باشد، مانند \(f'(x)\) در بالا، که یکی از انواع توابع زوج می باشد.)
این چهار نتیجۀ بدست آمده، به ترتیب؛ مثبت، منفی، منفی، و مثبت می باشند. اکنون به سراغ خط اعدادتان بروید، هر ناحیه از آن را با علامت مثبت یا منفی مناسب مشخص سازید، و نشان دهید که این تابع در کجاها افزایش می یابد (جایی که مشتق در آن مثبت باشد) و در کجاها کاهش می یابد (جایی که مشتق در آن منفی باشد). این نتیجه به اصطلاح نمودار علامت (sign graph) نامیده می شود. شکل 4-11 را ببینید. (چهار فلش رو به سمت راست در بالای این شکل به سادگی نشان می دهند که این "در حال افزایش" و "در حال کاهش" به شما می گویند همینطور که از چپ به راست می روید چه اتفاقی می افتد.)

ترجمۀ شکل:
increasing: در حال افزایش
decreasing: در حال کاهش
critical numbers: اعداد حیاتی
increasing: در حال افزایش
decreasing: در حال کاهش
critical numbers: اعداد حیاتی
شکل 4-11 به سادگی به شما می گوید اگر به نمودار \(f\) بنگرید چه چیزی را از روی آن خواهید دانست ـــ اینکه این تابع تا \(-2\) بالا می رود، از \(-2\) تا \(0\) پایین می رود، از \(0\) تا \(2\) پایینتر می رود، و دوباره از \(2\) بالا می رود.
این تابع در \(-2\) از درحال افزایش به در حال کاهش، تغییر می کند؛ به عبارت دیگر، شما تا \(-2\) بالا می روید و بعد از آن پایین می آیید. بنابراین در \(-2\) بالای یک تپه یا یک ماکزیمم موضعی دارید. برعکس، از آنجا که این تابع در \(2\) از در حال کاهش به در حال افزایش تغییر می کند، شما در آنجا ته یک دره یا یک مینیمم موضعی دارید. و از آنجا که علامت اولین مشتق در صفر تغییر نمی کند (از مثبت به منفی یا برعکس)، در این مقدار \(x\) نه یک مینیمم و نه یک ماکزیمم وجود دارد (وقتی این اتفاق می افتد، ـــ مانند همینجا ـــ شما معمولاً یک نقطۀ عطف افقی بدست می آورید).
آخرین مرحله اینست که با جایگذاری مقادیر \(x\) در تابع اصلی، مقادیر توابع، به عبارت دیگر ارتفاع ها، را برای این دو اکسترمم موضعی بدست آورید:
$$
f(x)=3x^5-20x^3 \\
f(-2)=3(-2)^5-20(-2)^3=64 \\
f(2)=3(2)^5-20(2)^3=-64
$$
بدین ترتیب، ماکزیمم موضعی در \((-2,64)\) و مینیمم موضعی در \((2,-64)\) قرار گرفته است. کار تمام است.
اکسترمم های موضعی در نقاط ناپیوستگی رخ نمی دهند. برای استفاده از آزمون مشتق اول برای آزمایش یک اکسترمم موضعی در یک عدد بحرانی خاص، آن تابع باید در آن مقدار \(x\) پیوسته باشد.
آزمون مشتق دوم (second derivative test)
آزمون مشتق دوم مبتنی بر دو مفهوم است: ابتدا اینکه در قلۀ یک تپه، یک جاده به شکل کوهان شتر (hump shape) می باشد ـــ به عبارت دیگر رو به سمت پایین خم می شود یا تقعر رو به پایین دارد؛ و دوم اینکه، در انتهای یک دره، یک جاده به شکل فنجان (cup-shaped) می باشد، بنابراین رو به سمت بالا خم می شود یا تقعر رو به بالا دارد.
تقعر یک تابع در یک نقطه با مشتق دوم آن بدست می آید: یک مشتق دوم مثبت بدین معناست که آن تابع در آنجا تقعر رو به بالا دارد، یک مشتق دوم منفی بدین معناست که آن تابع تقعر رو به پایین دارد، و یک مشتق دوم صفر بی نتیجه می باشد (این تابع می تواند تقعر رو به سمت بالا یا تقعر رو به سمت پایین داشته باشد، یا می تواند در آنجا یک نقطۀ عطف وجود داشته باشد). بنابراین، در تابع ما، \(f\)، تمام کاری که شما باید انجام دهید اینست که مشتق دوم آن را بیابید و سپس اعداد بحرانی پیدا شده را در آنها جایگذاری کنید، \(-2\)، \(0\)، و \(2\)، و توجه کنید که آیا نتایج شما مثبت، منفی، یا صفر می باشند. بعبارت دیگر:
$$
f(x)=3x^5-20x^3 \\
f'(x)=15x^4-60x^2 \\
f''(x)=60x^3-120x \\
f''(-2)=60(-2)^3-120(-2)=-240\\
f''(0)=60(0)^3-120(0)=0\\
f''(2)=60(2)^3-120(2)=240
$$
در \(x=-2\)، مشتق دوم، \((-240)\)، منفی می باشد. این به شما می گوید که \(f\) در جاییکه \(x\) برابر با \(-2\) می باشد، تقعر رو به پایین دارد، و بدین ترتیب در آنجا یک ماکزیمم نسبی وجود دارد. مشتق دوم، \((240)\)، در جاییکه \(x\) برابر با \(2\) است، مثبت می باشد، بنابراین \(f\) در آنجا تقعر رو به بالا دارد و بدین ترتیب یک مینیمم نسبی در \(x=2\) وجود دارد. از آنجا که مشتق دوم در \(x=0\) برابر با صفر می باشد، آزمون مشتق دوم برای این عدد بحرانی با شکست مواجه می شود ـــ این عدد صفر هیچ چیزی را در مورد تقعر در \(x=0\) یا اینکه آیا در آنجا یک ماکزیمم یا مینیمم نسبی وجود دارد یا خیر، به شما نمی گوید. وقتیکه این اتفاق می افتد، شما باید از آزمون مشتق اول استفاده کنید.
حالا در مثالی دیگر، یکبار دیگر وارد مراحل آزمون مشتق اول و دوم می شویم. اکسترمم های موضعی \(g(x)=2x-3x^{\frac{2}{3}} +4\) را بیابید. شکل 5-11 را ببینید.

-
اولین مشتق \(g\) را بیابید.
$$
g(x)=2x-3x^{\frac{2}{3}}+4 \\
g'(x)=2-2x^{-\frac{1}{3}}
$$
-
این مشتق را برابر با صفر قرار دهید و حل کنید.
$$
2-2x^{-\frac{1}{3}}=0 \\
-2x^{-\frac{1}{3}}=-2 \\
x^{-\frac{1}{3}}=1 \\
(x^{-\frac{1}{3}})^{-3}=1^{-3} \\
x=1
$$
بدین ترتیب \(1\) یک عدد حیاتی می باشد.
-
تعیین کنید که آیا مشتق اول به ازاء هر مقدار \(x\) تعریف نشده می باشد یا خیر.
\(2^{-\frac{1}{3}}\) برابر با \(\frac{2}{\sqrt[3]{x}}\) می باشد. حالا، از آنجا که ریشۀ سوم صفر برابر با صفر می باشد، اگر صفر را در \(\frac{2}{\sqrt[3]{x}}\) جایگذاری کنید، به نتیجۀ \(\frac{2}{0}\) می رسید، که تعریف نشده می باشد. بنابراین مشتق \(2-2x^{-\frac{1}{3}}\) در \(x=0\) تعریف نشده می باشد، و بدین ترتیب \(0\) عدد بحرانی دیگری می باشد. از مرحله های \(2\) و \(3\) ، شما به لیست کامل اعداد بحرانی می رسید: \(0\) و \(1\) .
-
این اعداد بحرانی را بر روی یک خط اعداد قرار دهید، و سپس از آزمون مشتق اول برای پیدا کردن علامت هر ناحیه استفاده کنید.
شما می توانید از \(-1\)، \(0.5\)، و \(2\) بعنوان اعداد آزمایشی استفاده کنید:
$$
g'(x)=2-2x^{-\frac{1}{3}} \\
g'(-1)=4 \\
g'(0.5) \approx -0.52 \\
g'(2) \approx 0.41
$$
شکل 6-11 این نمودار علامت (sign graph) را نشان می دهد.
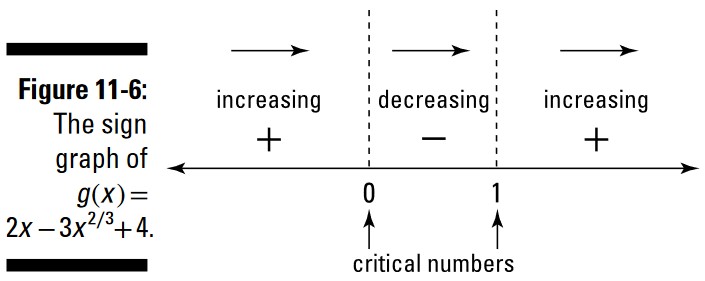
از آنجا که مشتق اول \(g\) در \(0\) از مثبت به منفی تغییر می کند، یک ماکزیمم نسبی در آنجا وجود دارد. و از آنجا که این مشتق اول در \(1\) از منفی به مثبت تغییر می کند، یک مینیمم نسبی در \(x=1\) وجود دارد.
-
این اعداد حیاتی را در \(g\) جایگذاری کنید تا مقادیر این تابع (ارتفاع ها) را در این دو اکسترمم موضعی بدست آورید.
$$g(x)=2x-3x^{\frac{2}{3}}+4 \\
g(0)=4\\
g(1)=3$$
بنابراین یک ماکزیمم موضعی در \((0,4)\) و یک مینیمم موضعی در \((1,3)\) وجود دارد. کار تمام است.
شما می توانید از آزمون مشتق دوم به جای آزمون مشتق اول در مرحلۀ 4 استفاده کنید. در ابتدا، به مشتق دوم \(g\) نیاز دارید، که همانطور که خودتان هم می دانید، برابر با مشتقِ مشتق اول آن می باشد:
$$
g'(x)=2-2x^{-\frac{1}{3}} \\
g''(x)=\frac{2}{3}x^{-\frac{4}{3}}
$$
مشتق دوم را در \(x=1\) ارزیابی کنید (این یک عدد بحرانی از مرحلۀ 2 می باشد):
$$g''(1)=\frac{2}{3}$$
از آنجا که \(g''(1)\) مثبت می باشد، شما می دانید که \(g\) در \(x=1\) تقعر رو به بالا دارد و ، بدین ترتیب، یک مینیمم نسبی در آنجا وجود دارد.
در عدد بحرانی دیگر، \(x=0\) (از مرحلۀ 3)، اولین مشتق تعریف نشده است. جایی که مشتق اول تعریف نشده باشد، آزمون مشتق دوم کمکی نخواهد کرد، شما باید از آزمون مشتق اول برای این عدد بحرانی استفاده کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: