خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
پیدا کردن اکسترمم های مطلق در فاصلۀ بسته

هر تابعی که در یک فاصلۀ بسته (closed interval) پیوسته می باشد، باید یک مقدار ماکزیمم مطلق و یک مقدار مینیمم مطلق در آن فاصله (بازه) داشته باشد ـــ به عبارت دیگر، یک بالاترین نقطه و پایین ترین نقطه ـــ همانطور که در مثال زیر می بینید، در آنجا می تواند یک الزام برای بالاترین و پایینترین مقدار وجود داشته باشد.

یافتن ماکزیمم مطلق (absolute max) و مینیمم مطلق (absolute min) به سادگی یک بشکن زدن است. تمام آنچه که شما انجام میدهید محاسبۀ اعداد بحرانی (critical numbers) آن تابع در فاصلۀ داده شده، تعیین ارتفاع تابع در هر عدد بحرانی، می باشد، و سپس محاسبه ارتفاع تابع در دو نقطه پایانی این فاصله است. بزرگترین در میان این مجموعه ارتفاع ها، ماکزیمم مطلق می باشد؛ و البته، کمترین یک مینیمم مطلق است. در اینجا مثالی داریم: ماکزیمم مطلق و مینیمم مطلق \(h(x)=\cos(2x)-2 \sin x\) را در فاصلۀ بستۀ \([\frac{\pi}{2},2\pi]\) بیابید.
ماکزیمم مطلق در دو نقطه رخ داده است: \(\biggl( \frac{7\pi}{6},1.5 \biggr)\) و \(\biggl( \frac{11\pi}{6},1.5 \biggr)\). مینیمم مطلق در یکی از این نقاط پایانی رخ داده است، \(\biggl( \frac{\pi}{2},-3 \biggr)\)، و بدین ترتیب یک اکسترمم نقطۀ پایانی (endpoint extremum) نامیده می شود.
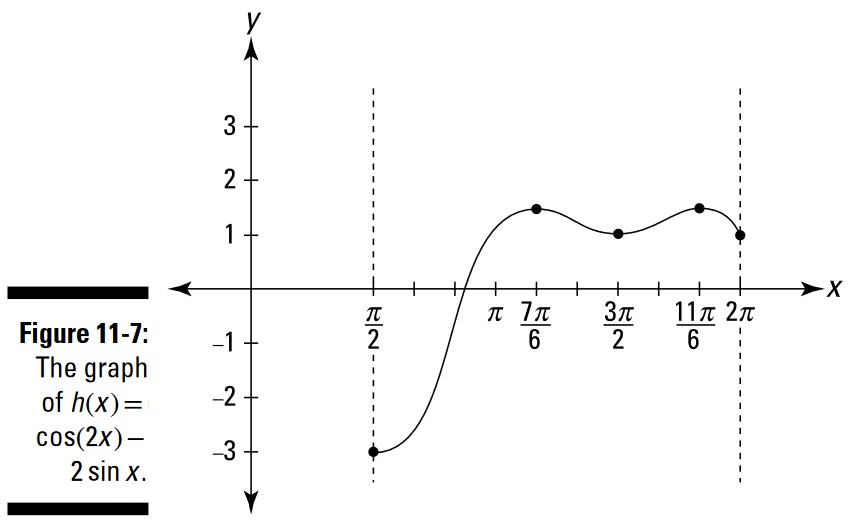
جدول 1-11 مقادیر \(h(x)=\cos (2x) - 2 \sin x\) را در سه عدد بحرانی در فاصلۀ \(\frac{\pi}{2}\) تا \(2\pi\) و در نقاط پایانی این فاصله نشان می دهد؛ شکل 7-11 نمودار \(h\) را نشان می دهد.

چند ملاحظه. ابتدا، همانطور که در شکل 7-11 می بینید، نقاط \(\biggl( \frac{7\pi}{6},1.5 \biggr)\) و \(\biggl( \frac{11\pi}{6},1.5 \biggr)\) هر دو ماکزیمم های نسبی \(h\) هستند، و نقطۀ \(\biggl( \frac{3\pi}{2},1 \biggr)\) یک مینیمم موضعی از \(h\) می باشد. با این حال، اگر فقط بخواهید اکسترمم های مطلق (absolute extrema) در یک فاصلۀ بسته (closed interval) را بیابید، نباید توجهی به این داشته باشید که این نقاط ماکزیمم یا مینیمم موضعی یا هیچکدام از این دو، هستند. و بدین ترتیب نباید خودتان را با استفاده کردن از آزمون مشتق اول یا دوم اذیت کنید. تمام کاری که باید انجام دهید اینست که ارتفاع در اعداد بحرانی و در نقاط پایانی را تعیین کنید و سپس بزرگترین و کوچکترین عدد را از این لیست انتخاب کنید. دوم اینکه، ماکزیمم مطلق و مینیمم مطلق در این بازه، هیچ چیزی در مورد اینکه این تابع بیرون از این بازه چگونه رفتار می کند را به شما نمی گوید. به عنوان مثال، تابع \(h\)، ممکن است بیرون از این بازه از ارتفاع \(1.5\) بالاتر برود یا از ارتفاع \(-3\) پایینتر بیاید.

یک فاصلۀ بسته مانند \([2,5]\) شامل نقاط پایانی \(2\) و \(5\) می گردد. یک فاصلۀ باز (open interval) مانند \((2,5)\) نقاط پایانی را مستثنی می کند.
یافتن ماکزیمم مطلق (absolute max) و مینیمم مطلق (absolute min) به سادگی یک بشکن زدن است. تمام آنچه که شما انجام میدهید محاسبۀ اعداد بحرانی (critical numbers) آن تابع در فاصلۀ داده شده، تعیین ارتفاع تابع در هر عدد بحرانی، می باشد، و سپس محاسبه ارتفاع تابع در دو نقطه پایانی این فاصله است. بزرگترین در میان این مجموعه ارتفاع ها، ماکزیمم مطلق می باشد؛ و البته، کمترین یک مینیمم مطلق است. در اینجا مثالی داریم: ماکزیمم مطلق و مینیمم مطلق \(h(x)=\cos(2x)-2 \sin x\) را در فاصلۀ بستۀ \([\frac{\pi}{2},2\pi]\) بیابید.
-
اعداد بحرانی \(h\) در فاصلۀ باز \((\frac{\pi}{2},2\pi)\) را بیابید.
(اگر دانش شما در مورد توابع مثلثاتی نیاز به تازه سازی داشته باشد، فصل 6 را ببینید.)
$$
\begin{array}{c c}
h(x)=\cos (2x)-2\sin x &\\
h'(x)=-\sin(2x) \cdot 2 - 2 \cos x &\\
0=-2 \sin(2x) - 2 \cos x &\\
0 = \sin(2x) + \cos x &\\
0= 2\sin x \cos x + \cos x &\\
0= \cos x(2 \sin x+1) &\\
\cos x = 0 & \text{ or } 2 \sin x +1=0 &\\
x=\frac{3\pi}{2} & \sin x=-\frac{1}{2} \\
& x=\frac{7\pi}{6}, \frac{11\pi}{6}
\end{array}
$$
بدین ترتیب، صفرهای \(h'\) برابر با \(\frac{7\pi}{6}\)، \(\frac{3\pi}{2}\)، و \(\frac{11\pi}{6}\) می باشند، و از آنجا که \(h'\) برای تمامی مقادیر ورودی تعریف شده می باشد، این لیست کامل اعداد بحرانی می باشد.
-
مقادیر تابع (ارتفاع ها) را به ازاء هر عدد بحرانی (critical number) محاسبه کنید.
$$h(x)=\cos(2x)-2 \sin x \\
h(\frac{7\pi}{6})=\cos(2 \cdot \frac{7\pi}{6})-2 \sin (\frac{7\pi}{6}) \\
=0.5-2 \cdot (-0.5) = 1.5 \\
h(\frac{3\pi}{2})=\cos(2 \cdot \frac{3\pi}{2})-2 \sin (\frac{3\pi}{2}) \\
=-1-2 \cdot (-1) = 1 \\
h(\frac{11\pi}{6})=\cos(2 \cdot \frac{11\pi}{6})-2 \sin (\frac{11\pi}{6}) \\
=0.5 - 2 \cdot (-0.5)=1.5$$
-
مقادیر تابع را در نقاط پایانی فاصله (بازه) تعیین کنید.
$$
h(\frac{\pi}{2})=\cos(2 \cdot \frac{\pi}{2})-2 \sin (\frac{\pi}{2}) \\
=-1-2 \cdot 1 = -3 \\
h(2\pi)=\cos(2 \cdot 2\pi)-2 \sin (2\pi) \\
=1-2 \cdot 0 =1
$$
خوب، از مراحل 2 و 3، شما پنج ارتفاع را یافته اید: \(1.5\)، \(1\)، \(1.5\)، \(-3\)، و \(1\). بزرگترین عدد در این لیست، \(1.5\)، برابر با ماکزیمم مطلق (absolute max) می باشد؛ کوچکترین عدد، \(-3\)، برابر با مینمم مطلق (absolute min) می باشد.
ماکزیمم مطلق در دو نقطه رخ داده است: \(\biggl( \frac{7\pi}{6},1.5 \biggr)\) و \(\biggl( \frac{11\pi}{6},1.5 \biggr)\). مینیمم مطلق در یکی از این نقاط پایانی رخ داده است، \(\biggl( \frac{\pi}{2},-3 \biggr)\)، و بدین ترتیب یک اکسترمم نقطۀ پایانی (endpoint extremum) نامیده می شود.
جدول 1-11 مقادیر \(h(x)=\cos (2x) - 2 \sin x\) را در سه عدد بحرانی در فاصلۀ \(\frac{\pi}{2}\) تا \(2\pi\) و در نقاط پایانی این فاصله نشان می دهد؛ شکل 7-11 نمودار \(h\) را نشان می دهد.

چند ملاحظه. ابتدا، همانطور که در شکل 7-11 می بینید، نقاط \(\biggl( \frac{7\pi}{6},1.5 \biggr)\) و \(\biggl( \frac{11\pi}{6},1.5 \biggr)\) هر دو ماکزیمم های نسبی \(h\) هستند، و نقطۀ \(\biggl( \frac{3\pi}{2},1 \biggr)\) یک مینیمم موضعی از \(h\) می باشد. با این حال، اگر فقط بخواهید اکسترمم های مطلق (absolute extrema) در یک فاصلۀ بسته (closed interval) را بیابید، نباید توجهی به این داشته باشید که این نقاط ماکزیمم یا مینیمم موضعی یا هیچکدام از این دو، هستند. و بدین ترتیب نباید خودتان را با استفاده کردن از آزمون مشتق اول یا دوم اذیت کنید. تمام کاری که باید انجام دهید اینست که ارتفاع در اعداد بحرانی و در نقاط پایانی را تعیین کنید و سپس بزرگترین و کوچکترین عدد را از این لیست انتخاب کنید. دوم اینکه، ماکزیمم مطلق و مینیمم مطلق در این بازه، هیچ چیزی در مورد اینکه این تابع بیرون از این بازه چگونه رفتار می کند را به شما نمی گوید. به عنوان مثال، تابع \(h\)، ممکن است بیرون از این بازه از ارتفاع \(1.5\) بالاتر برود یا از ارتفاع \(-3\) پایینتر بیاید.

لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: