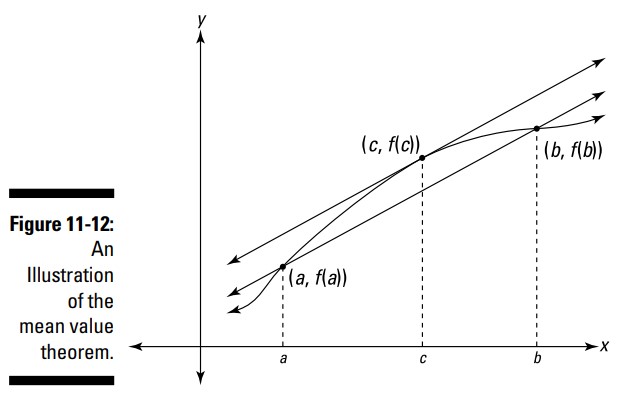
شما از قضیۀ مقدار میانی (Mean Value Theorem) زیاد استفاده نخواهید کرد، اما این یک قضیۀ معروف است ـــ یکی از دو یا سه قضیۀ خیلی مهم در حسابان ـــ بنابراین شما واقعاً باید آن را بیاموزید. آن بسیار ساده است و یک ارتباط زیبا با قضیۀ مقدار میانی برای انتگرال ها که در فصل 17 به شما نشان خواهم داد، دارد. شکل 12-11 را ببینید.






در اینجا تعریف رسمی این قضیه را داریم.


اکنون به سراغ این تعریف به زبان ساده می رویم. ابتدا باید مراقب باشید که شکل چاپی شما خوب باشد. نیازمندی های این قضیه که این تابع باید پیوسته و قابل مشتق گیری باشد، صرفاً تضمین می کند که این یک تابع معمولی و روان بدون حفره ها یا گوشه ها باشد. اما از آنجا که تنها تعداد کمی تابع عجیب و غریب دارای حفره ها یا گوشه ها می باشند، شما اغلب نیاز نیست تا در مورد این نقاط خوب نگران باشید.

در اینجا معنای این قضیه را می بینید. خط قاطعی (secant line) که نقاط \(\biggl( a,f(a) \biggr)\) را به \(\biggl( b,f(b) \biggr)\) در شکل 12-11 متصل می کند، دارای شیبی است که از فرمول زیر بدست می آید:
$$\text{Slope}=\frac{y_2 - y_1}{x_2 - x_1} \\
= \frac{f(b)-f(a)}{b-a}$$
توجه داشته باشید که این با سمت راست معادلۀ قضیۀ مقدار میانی، یکسان می باشد. مشتق در یک نقطه همان شیب خط مماس در آن نقطه می باشد، بنابراین این قضیه صرفاً بیان می کند که دست کم باید یک نقطه بین \(a\) و \(b\) باشد که در آن شیب خط مماس با شیب خط قاطع بین \(a\) و \(b\) یکسان است. نتیجه خطوط موازی می باشد، مانند چیزی که در شکل 12-11 می بینید.

چرا باید چنین باشد؟ در اینجا یک استدلال بصری داریم. تجسم کنید خط قاطعی که \(\bigl( a,f(a) \bigr)\) و \(\bigl( b,f(b) \bigr)\) را متصل کرده است، بگیرید، و سپس آن را به سمت بالا سر بدهید و آن را با خط قاطع اصلی موازی نگهدارید. آیا می توانید ببینید که این دو نقطۀ تقاطع بین این خط سر خورده و تابع ـــ دو نقطه ای که در \(\bigl( a,f(a) \bigr)\) و \(\bigl( b,f(b) \bigr)\) آغاز می گردند ـــ به تدریج به یکدیگر نزدیک و نزدیکتر می شوند تا اینکه در نقطۀ \(\bigl( c,f(c) \bigr)\) به یکدیگر برسند؟ اگر این خط را بیشتر بالا ببرید، به طور کل از این تابع جدا می شوید. در این آخرین نقطۀ تقاطع، \(\bigl( c,f(c) \bigr)\) ، خط سُر خورده در یک نقطه این تابع را لمس می کند، و از اینرو خط مماسی بر این تابع در آن نقطه می باشد، و دارای شیب یکسانی با خط قاطع اصلی می باشد. این توضیحات اندکی بیش از حد ساده شده است، اما کفایت می کند.

در اینجا یک نوع کاملاً متفاوت از استدلال را داریم که باید به عقل سلیم خود متوسل شوید. اگر تابع موجود در شکل 12-11 کیلومتر شمار خودروی شما را در تابعی از زمان بخواند، سپس شیب این خط قاطع از \(a\) تا \(b\) سرعت میانگین (average speed) شما را در آن بازه از زمان به شما می دهد، زیرا تقسیم کردن مسیر پیموده شده، \(f(b)-f(a)\)، بر زمان سپری شده، \(b-a\)، سرعت میانگین را نتیجه می دهد. نقطۀ \(\bigl( c,f(c) \bigr)\)، نقطه ای است که در آن سرعت لحظه ای (instantaneous speed) شما ـــ که با مشتق \(f'(c)\) بدست می آید ـــ با سرعت میانگین شما برابر است.

حالا، فرض کنید که شما مشغول رانندگی هستید و با سرعت میانگین \(50\) مایل بر ساعت حرکت می کنید. قضیۀ مقدار میانی گارانتی می کند که شما دست کم یک لحظه در طول رانندگی تان \(50\) مایل بر ساعت می رانید. در موردش فکر کنید. اگر شما کل مسیر را کمتر از \(50\) مایل بر ساعت برانید، یا اگر کل مسیر را بیشتر از \(50\) مایل بر ساعت برانید، میانگین سرعت شما نمی تواند \(50\) مایل بر ساعت باشد. برای میانگین \(50\) مایل بر ساعت، شما باید یا در طول کل مسیر دقیقاً با سرعت \(50\) مایل بر ساعت برانید، یا بخشی از مسیر را با سرعتی کمتر از \(50\) مایل بر ساعت و بخش دیگری را بیشتر از این سرعت برانید. و اگر شما در یک نقطه کمتر از \(50\) مایل بر ساعت برانید و در نقطۀ دیگری بیشتر از آن سرعت برانید (یا برعکس این)، شما در هنگام سرعت گرفتن (یا هنگام کاهش سرعت) دست کم یک مرتبه به سرعت دقیق \(50\) رسیده اید. شما نمی توانید از روی \(50\) بپرید ـــ مانند اینکه یک لحظه \(49\) و لحظۀ دیگر \(51\) باشید ـــ زیرا سرعت با لغزیدن بر روی درجه ها بالا می رود، و نه پرش از روی آنها. در برخی نقاط سرعت سنج شما از \(50\) عبور می کند، و دست کم در یک لحظه، شما دقیقاً با سرعت \(50\) مایل بر ساعت رانندگی می کنید. این تمام چیزی است که قضیۀ مقدار میانی بیان می دارد.