خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مسأله های بهینه سازی (Optimization Problems)

در مقدمه، به شما گفتم که حسابان جهان را به بی شمار روش مختلف تغییر داده است، تاثیر آن محدود به بُرج عاج ریاضیات نمی باشد، بلکه تمامی پیرامون ما به صورت کاربردی چیزهایی مانند اجاق های مایکروویو، تلفن های همراه، و خودروها، را تحت تاثیر قرار داده است. خوب، اکنون فصل 12 است، و من سرانجام آماده ام تا به شما نشان دهم چگونه از حسابان برای حل کردن چندین مسالۀ کاربردی استفاده کنید.

یکی از کاربردی ترین استفاده های مشتق گیری (دیفرانسیل گیری) یافتن مقدار ماکزیمم یا مینیمم یک تابع در دنیای واقعی می باشد: ماکزیمم تولید یک کارخانه، ماکزیمم استحکام یک تیر آهن، مینیمم زمان مورد نیاز برای تکمیل کردن یک وظیفه، ماکزیمم برد یک موشک، و به همین ترتیب. بیایید با چند مثال استاندارد هندسی کار را آغاز کنیم.
همانطور که در شکل 1-12 می بینید، یک جعبۀ بدون رویه، با بریدن و تا کردنِ یک تکه مقوای \(30\) اینچ در \(30\) اینچ ساخته شده است.
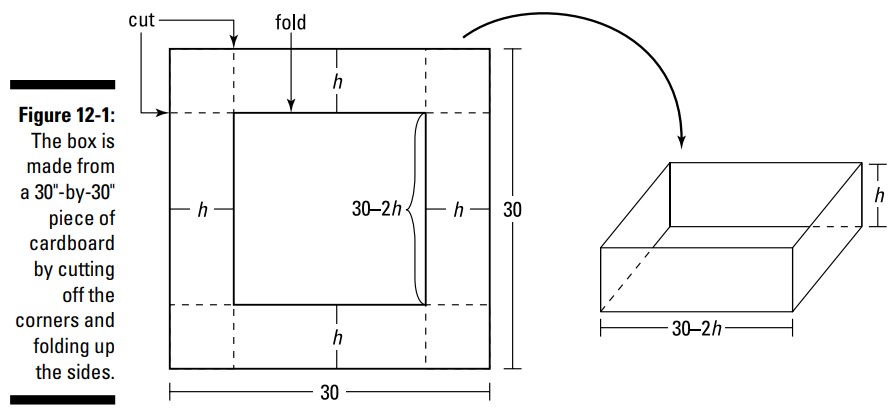
چه ابعادی یک جعبه با ماکزیمم حجم ممکن را می سازند؟ ریاضیات معمولاً انتزاعی و غیرکاربردی به نظر می رسد، اما در اینجا یک مسالۀ واقعیِ کاربردی داریم (خوب ... تقریباً). اگر یک تولید کننده بتواند جعبه های بزرگتر را به قیمت بیشتری بفروشد و \(100,000\) جعبه بسازد، شما بهتر است باور کنید که او پاسخ دقیق این سوال را می خواهد. در اینجا چگونگی حل آن را می بینید:
بنابراین، یک ارتفاع \(5\) اینچی، این جعبه را با ماکزیمم حجم ممکن (\(2,000\) اینچ مکعب) تولید می کند. از آنجا که طول و عرض برابر با \(30-2h\) می باشند، یک ارتفاع \(5\) یک طول و عرض \(30-2 \cdot 5 = 20\) را نتیجه می دهد، و از این رو ابعاد جعبۀ مطلوب عبارت از \(5 \times 20 \times 20\) می باشند. تمام شد.
یک گله دار استطاعت خرید \(300\) فوت حصار را دارد و می خواهد با این حصارها یک آغل بسازد و آن را به دو مستطیل مساوی تقسیم کند. شکل 2-12 را ببینید.
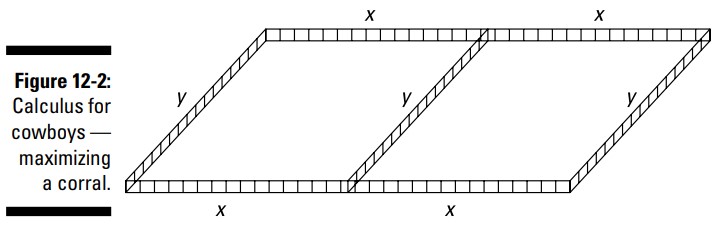
چه ابعادی مساحت این آغُل را به ماکزیمم مساحت ممکن می رساند؟ این مسالۀ کاربردی دیگری می باشد. این گله دار می خواهد با توجه به طول حصاری که استطاعت خریدش را دارد، بیشترین فضای ممکن را به حیواناتش بدهد. مانند بیشتر تجار او می خواهد بیشترین بهرۀ ممکنه را از پولش ببرد.
مقدار ماکزیمم این بازه برابر با \(3,750\) است، و بدین ترتیب، یک مقدار \(x\) برابر با \(37.5\) فوت، مساحت این آغل را با ماکزیمم مساحت ممکن آن می رساند. طول برابر با \(2x\)، یا \(75\) فوت می باشد. عرض برابر با \(y\) که برابر با \(100-\frac{4}{3}x\) است، می باشد. با جایگذاری \(37.5\) به \(100-\frac{4}{3}(37.5)=50\) می رسید. بنابراین این دامدار یک آغُل \(75 \times 50\) با مساحت \(3,750\) فوت مربع می سازد.

مسأله های بهینه سازی (Optimization Problems)
یکی از کاربردی ترین استفاده های مشتق گیری (دیفرانسیل گیری) یافتن مقدار ماکزیمم یا مینیمم یک تابع در دنیای واقعی می باشد: ماکزیمم تولید یک کارخانه، ماکزیمم استحکام یک تیر آهن، مینیمم زمان مورد نیاز برای تکمیل کردن یک وظیفه، ماکزیمم برد یک موشک، و به همین ترتیب. بیایید با چند مثال استاندارد هندسی کار را آغاز کنیم.
ماکزیمم حجم یک جعبه
همانطور که در شکل 1-12 می بینید، یک جعبۀ بدون رویه، با بریدن و تا کردنِ یک تکه مقوای \(30\) اینچ در \(30\) اینچ ساخته شده است.

چه ابعادی یک جعبه با ماکزیمم حجم ممکن را می سازند؟ ریاضیات معمولاً انتزاعی و غیرکاربردی به نظر می رسد، اما در اینجا یک مسالۀ واقعیِ کاربردی داریم (خوب ... تقریباً). اگر یک تولید کننده بتواند جعبه های بزرگتر را به قیمت بیشتری بفروشد و \(100,000\) جعبه بسازد، شما بهتر است باور کنید که او پاسخ دقیق این سوال را می خواهد. در اینجا چگونگی حل آن را می بینید:
-
چیزی را که به شکل ماکزیمم شده می خواهید، حجم، را به عنوان تابعی از مجهول، ارتفاع جعبه (که با طول برش یکی است)، بیان کنید.
$$
V=l \cdot w \cdot h \\
V(h)=(30-2h)(30-2h) \cdot h \\
=(900-120h+4h^2) \cdot h \\
=4h^3 - 120h^2 + 900h
$$
-
دامنۀ تابعتان را تعیین کنید.
ارتفاع نمی تواند منفی باشد، و از آنجا که طول (و عرض) این جعبه برابر با \(30-2h\) می باشد، که نمی تواند عددی منفی باشد، \(h\) نمی تواند بزرگتر از \(15\) باشد. بنابراین، مقادیر معقول برای \(h\) عبارت از \(0 \le h \le 15\) می باشند. شما هم اکنون می خواهید مقدار ماکزیمم \(V(h)\) را در این بازه بیابید. از روش "یافتن ماکزیمم مطلق در یک بازۀ بسته" که در فصل 11 آموزش داده شد، استفاده کنید.
-
با برابر صفر قرار دادن مشتق این تابع و حل کردن آن، اعداد بحرانی (critical numbers) تابع \(V(h)\) را در بازۀ باز \((0,15)\) بدست آورید. و فراموش نکنید که اعدادی را که به ازاء آنها مشتق تعریف نشده (undefined) می باشد، بررسی کنید.
$$V(h)=4h^3-120h^2+900h \\
V'(h)=12h^2-240h+900 \\
0=12h^2-240h+900 \\
0=h^2-20h+75 \\
0=(h-15)(h-5) \\
h=15 \text{ or } 5$$
از آنجا که \(15\) در بازۀ باز \((0,15)\) نمی باشد، به عنوان یک عدد بحرانی واجد شرایط شناخته نمی شود (هر چند این یک نکتۀ قابل بحث است زیرا به هر حال در مرحلۀ 4 آن را تست خواهید کرد). و از آنجا که این مشتق به ازاء تمامی مقادیر ورودی تعریف شده است، بدین ترتیب، مسلماً هرگز تعریف نشده نخواهد بود، در نتیجه اعداد بحرانی دیگری نداریم. بنابراین، \(5\) تنها عدد بحرانی ما می باشد.
-
این تابع را در عدد بحرانی، \(5\) ، و در نقاط پایانی بازه، \(0\) و \(15\) ، ارزیابی کنید، تا ماکزیمم این تابع را بیابید.
$$V(h)=4h^3-120h^2+900h \\
V(0)=0 \\
V(5)=2000 \\
V(15)=0$$
نقاط پایانی را بیازمایید. اکسترممی (extremum) که بدنبال آن هستید معمولاً در نقاط پایانی رخ نمی دهد، اما می تواند در آنجا هم باشد ـــ بنابراین از ارزیابی تابع در دو نقطۀ پایانی بازه، غفلت نکنید.
بنابراین، یک ارتفاع \(5\) اینچی، این جعبه را با ماکزیمم حجم ممکن (\(2,000\) اینچ مکعب) تولید می کند. از آنجا که طول و عرض برابر با \(30-2h\) می باشند، یک ارتفاع \(5\) یک طول و عرض \(30-2 \cdot 5 = 20\) را نتیجه می دهد، و از این رو ابعاد جعبۀ مطلوب عبارت از \(5 \times 20 \times 20\) می باشند. تمام شد.
ماکزیمم مساحت یک آغُل
یک گله دار استطاعت خرید \(300\) فوت حصار را دارد و می خواهد با این حصارها یک آغل بسازد و آن را به دو مستطیل مساوی تقسیم کند. شکل 2-12 را ببینید.

چه ابعادی مساحت این آغُل را به ماکزیمم مساحت ممکن می رساند؟ این مسالۀ کاربردی دیگری می باشد. این گله دار می خواهد با توجه به طول حصاری که استطاعت خریدش را دارد، بیشترین فضای ممکن را به حیواناتش بدهد. مانند بیشتر تجار او می خواهد بیشترین بهرۀ ممکنه را از پولش ببرد.
-
-
چیزهایی را که به صورت ماکزیمم می خواهید (مساحت) را به شکل تابعی از دو مجهول (\(x\) و \(y\)) بیان کنید.
$$A=l \cdot w \\
=(2x)(y)$$
در مثال جعبۀ مقوایی در بخش قبلی، شما بسادگی می توانید حجم را به شکل تابعی از یک متغیر بنویسید ـــ که همیشه چیزی است که شما نیاز دارید. اما در اینجا، مساحت تابعی از دو متغیر می باشد (\(x\) و \(y\))، بنابراین مرحلۀ 1 دو مرحلۀ فرعی دیگر دارد که یکی از این متغیرها را حذف می کند.
-
از اطلاعات داده شده استفاده کنید تا این دو متغیر را به یکدیگر مرتبط کنید.
حصار \(300\) فوتی برای سه بخش استفاده می گردد، بنابراین:
$$300=x+x+x+x+y+y+y \\
300 = 4x+3y$$
-
این معادله را برای بدست آوردن \(y\) حل کنید و نتیجۀ بدست آمده برای \(y\) را در معادلۀ مرحلۀ \(1.a\) جایگذاری کنید. این چیزی را که نیاز دارید به شما می دهد ـــ یک تابع از یک متغیر.
$$4x+3y=300 \\
3y=300-4x \\
y=\frac{300-4x}{3} \\
y=100-\frac{4}{3}x$$
$$A=(2x)(y) \\
A(x)=(2x)(100-\frac{4}{3}x) \\
A(x)=200x-\frac{8}{3}x^2$$
-
چیزهایی را که به صورت ماکزیمم می خواهید (مساحت) را به شکل تابعی از دو مجهول (\(x\) و \(y\)) بیان کنید.
$$A=l \cdot w \\
-
دامنۀ این تابع را تعیین کنید.
شما نمی توانید حصاری با طول منفی داشته باشید، بنابراین \(x\) نمی تواند منفی باشد، و بزرگترین مقدار \(x\) برابر با \(300\) تقسیم بر \(4\)، یا \(75\) می باشد. بنابراین، \(0 \le x \le 75\) .
-
اعداد بحرانی \(A(x)\) در بازۀ باز \((0,75)\) را با قرار دادن مشتق آن برابر با صفر بیابید و آن را حل کنید (و بررسی کنید که آیا این مشتق در جایی از این بازه تعریف نشده است یا خیر).
$$A(x)=200x-\frac{8}{3}x^2 \\
A'(x)=200-\frac{16}{3}x \\
0=200-\frac{16}{3} x \\
\frac{16}{3} x=200 \\
x=200 \cdot \frac{3}{16} \\
=37.5$$
از آنجا که \(A'\) به ازاء تمامی مقادیر \(x\) تعریف شده می باشد، \(37.5\) تنها عدد بحرانی ما می باشد.
-
این تابع را در عدد بحرانی، \(37.5\) ، و در نقاط پایانی بازه، \(0\) و \(75\) ، ارزیابی کنید.
$$A(x)=200x-\frac{8}{3}x^2 \\
A(0)=0 \\
A(37.5)=3750 \\
A(75)=0$$
توجه: ارزیابی یک تابع در نقاط پایانی یک بازۀ بسته یک مرحلۀ استاندارد در یافتن یک اکسترمم مطلق در آن بازه می باشد. با این حال، اگر متوجه شده اید که \(A(x)\) یک سهمی سروته می باشد و از اینرو قلۀ آن در \((37.5,3750)\) باید بالاتر از هر کدام از نقاط پایانی آن باشد ، شما می توانید این مرحله را در اینجا نادیده بگیرید.
مقدار ماکزیمم این بازه برابر با \(3,750\) است، و بدین ترتیب، یک مقدار \(x\) برابر با \(37.5\) فوت، مساحت این آغل را با ماکزیمم مساحت ممکن آن می رساند. طول برابر با \(2x\)، یا \(75\) فوت می باشد. عرض برابر با \(y\) که برابر با \(100-\frac{4}{3}x\) است، می باشد. با جایگذاری \(37.5\) به \(100-\frac{4}{3}(37.5)=50\) می رسید. بنابراین این دامدار یک آغُل \(75 \times 50\) با مساحت \(3,750\) فوت مربع می سازد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: