خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مسأله های تانژانت و خط نرمال

در این فصل، سه کاربرد دیگر مشتق گیری را خواهید دید: مسأله های تانژانت و خط نرمال (tangent and normal line)، مسأله های تقریب خطی (linear approximation)، و مسأله های اقتصادی (economics). موضوع مشترکی که این مسأله ها را به یکدیگر گره می زند، مفهوم یک خط مماس بر یک منحنی می باشد ـــ که نباید همراه با هیچ تعجبی باشد، زیرا معنی مشتق یک منحنی، شیب آن خط مماس می باشد.

تا اینجا شما می دانید که یک خط مماس (تانژانت) بر روی یک منحنی چگونه است. یک خط نرمال (normal line) به سادگی یک خط است که در نقطۀ تماس (point of tangency)، بر یک خط مماس، عمود است. مسأله های شامل تانژانت ها و نرمال ها، کاربردهای رایجی از مشتق گیری می باشند.
مثال: نقطۀ تماس خطهایی که که از نقاط \((1,-1)\) می گذرند و بر سهمیِ \(y=x^2\) مماس می باشند را بیابید.
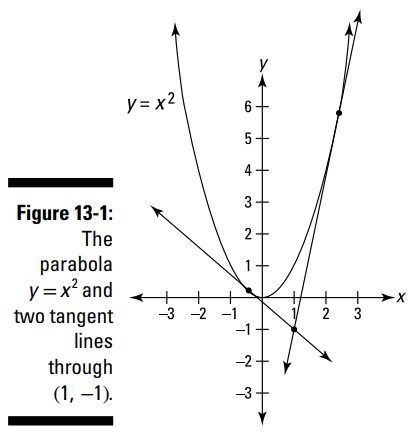
پاسخ: اگر نمودار این سهمی را بکشید و این نقطه را بر روی آن قرار دهید، می توانید ببینید که دو روش برای ترسیم یک خط مماس از \((1,-1)\) وجود دارد: به سمت بالا و راست، و به سمت بالا و چپ. شکل 1-13 را ببینید.
کلید حل این مسأله، معنای مشتق (derivative) می باشد: فراموش نکنید که مشتق یک تابع در یک نقطۀ مشخص برابر با شیب آن خط مماس در آن نقطه می باشد. بنابراین، تمام کاری که باید انجام دهید اینست که مشتق این سهمی را برابر با شیب آن خط مماس قرار دهید و آن را حل کنید:
در اینجا مسأله ای داریم که مکمل مسالۀ خط تانژانت ارائه شده در بخش قبلی است. نقاط تعامد (points of perpendicularity) برای تمامی خطوط نرمال در سهمیِ \(y=\frac{1}{16}x^2\)، که از نقطۀ \((3,15)\) عبور می کنند را بیابید.
نمودار این سهمی را ترسیم کنید و نقطۀ \((3,15)\) را بر روی آن قرار دهید. اکنون، قبل از انجام عملیات ریاضی، سعی کنید تا موقعیت تمامی خطوط نرمال را برآورد کنید. چند خط نرمال می بینید؟ مشاهدۀ اینکه از نقطۀ \((3,15)\) یک خط نرمال به سمت پایین و راست می رود بسیار آسان است، و خط نرمال دیگری رو به پایین و سمت چپ می رود. اما واقعاً آن خط نرمال دومی که رو به سمت پایین و چپ می رود را دیدید؟ اگر آن را ندیدید، نگران نباشید، زیرا هنگامی که عملیات ریاضی را انجام دهید، به هر سه پاسخ می رسید.
شکل 2-13 این سهمی و این سه خط نرمال را نشان می دهد.
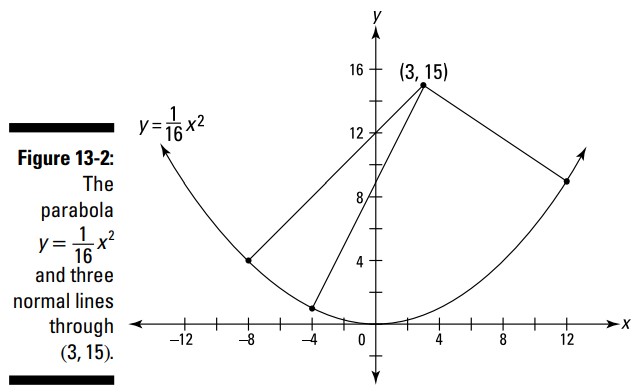
با نگاه کردن به این شکل، شما می توانید از میزان کاربردی بودن این مسأله قدردانی کنید. اگر بر حسب تصادف خودتان را در جایی بیابید که درون یک دیوار سهمی ایستاده باشید، و بخواهید محل دقیق سه نقطه ای بر روی این دیوار را بیابید که می توانید یک توپ را به آنجا پرتاب کنید و مستقیماً به سمت خودتان و رو به عقب باز گردد، در آن صورت این مسأله واقعاً سودمند خواهد بود.
راه حل این مسأله، بسیار شبیه به راه حل مسالۀ خط تانژانت می باشد، با این استثناء که در این مسأله شما از قانون خطهای متعامد (perpendicular lines) استفاده می کنید:
هر خط نرمال در شکل 2-13 بر خط تانژانتی که در آن نقطه رسم می شود، عمود است. بنابراین شیب هر خط نرمال کسرمتقابل مخالف (قرینۀ معکوس) شیب خط تانژانت متناظرش می باشد ـــ که مسلماً با مشتق بدست می آید. بنابراین راه حل اینگونه خواهد بود:

تانژانت ها و خط های نرمال
تا اینجا شما می دانید که یک خط مماس (تانژانت) بر روی یک منحنی چگونه است. یک خط نرمال (normal line) به سادگی یک خط است که در نقطۀ تماس (point of tangency)، بر یک خط مماس، عمود است. مسأله های شامل تانژانت ها و نرمال ها، کاربردهای رایجی از مشتق گیری می باشند.
مسالۀ خط تانژانت
مثال: نقطۀ تماس خطهایی که که از نقاط \((1,-1)\) می گذرند و بر سهمیِ \(y=x^2\) مماس می باشند را بیابید.
پاسخ: اگر نمودار این سهمی را بکشید و این نقطه را بر روی آن قرار دهید، می توانید ببینید که دو روش برای ترسیم یک خط مماس از \((1,-1)\) وجود دارد: به سمت بالا و راست، و به سمت بالا و چپ. شکل 1-13 را ببینید.

کلید حل این مسأله، معنای مشتق (derivative) می باشد: فراموش نکنید که مشتق یک تابع در یک نقطۀ مشخص برابر با شیب آن خط مماس در آن نقطه می باشد. بنابراین، تمام کاری که باید انجام دهید اینست که مشتق این سهمی را برابر با شیب آن خط مماس قرار دهید و آن را حل کنید:
-
از آنجا که معادلۀ این سهمی برابر با \(y=x^2\) می باشد، می توانید یک نقطۀ عمومی بر روی این سهمی در نظر بگیرید، \((x,y)\)، و \(x^2\) را جایگزین \(y\) کنید.
بنابراین، این دو نقطۀ تماس را با \((x,x^2)\) برچسب گذاری کنید.
-
مشتق این سهمی را بگیرید.
$$y=x^2 \\
y'=2x$$
-
با استفاده از فرمول شیب، \(\frac{y_2 - y_1}{x_2-x_1}\)، شیب هر خط مماس را از \((1,-1)\) تا \((x,x^2)\) برابر با مشتق در \((x,x^2)\) که \(2x\) است، قرار دهید، و آن را برای بدست آوردن \(x\) حل کنید.
در ضمن، اگر به عملیات ریاضی که در این مرحله انجام می دهید به عنوان کاربردن آن صرفاً بر روی یکی از این خطوط مماس فکر کنید، ممکن است برای شما معنادارتر باشد ـــ فرض کنید خط مماسی که رو به سمت بالا و راست می رود ـــ اما در واقع این عملیات ریاضی به صورت همزمان بر روی هر دوی این خطهای مماس اِعمال می گردد.
$$\frac{y_2 - y_1}{x_2-x_1} = y' \\
\frac{x^2 - (-1)}{x-1} = 2x \\
x^2 - (-1) = 2x(x-1) \\
x^2+1=2x^2 - 2x \\
0 = x^2 - 2x - 1 \\
x=\frac{2 \pm \sqrt{(-2)^2 - 4(1)(-1)}}{2 \cdot 1} \\
=\frac{2 \pm \sqrt{8}}{2} \\
= \frac{2 \pm 2 \sqrt{2}}{2} \\
= 1 \pm \sqrt{2}
$$
بنابراین، مختصات \(x\) ها در نقاط تماس برابر با \(1+\sqrt{2}\) و \(1-\sqrt{2}\) می باشند.
-
هر کدام از این مختصات های \(x\) را در \(y=x^2\) جایگذاری کنید تا مختصات \(y\) آن را بدست آورید.
$$y=(1+\sqrt{2})^2 \\
=1+2\sqrt{2}+2 \\
=3+2\sqrt{2}$$
$$y=(1-\sqrt{2})^2 \\
=1-2\sqrt{2}+2 \\
=3-2\sqrt{2}$$
بدین ترتیب، این دو نقطۀ تماس عبارت از \((1+\sqrt{2},3+2\sqrt{2})\) و \((1-\sqrt{2},3-2\sqrt{2})\)، یا در حدود \((2.4,5.8)\) و \((-0.4,0.2)\) می باشند.
مسالۀ خط نرمال
در اینجا مسأله ای داریم که مکمل مسالۀ خط تانژانت ارائه شده در بخش قبلی است. نقاط تعامد (points of perpendicularity) برای تمامی خطوط نرمال در سهمیِ \(y=\frac{1}{16}x^2\)، که از نقطۀ \((3,15)\) عبور می کنند را بیابید.
تعریف خط نرمال (normal line): یک خط نرمال بر یک منحنی در یک نقطۀ مشخص، خط عمود بر خطی است که در همان نقطه تانژانت منحنی است.
نمودار این سهمی را ترسیم کنید و نقطۀ \((3,15)\) را بر روی آن قرار دهید. اکنون، قبل از انجام عملیات ریاضی، سعی کنید تا موقعیت تمامی خطوط نرمال را برآورد کنید. چند خط نرمال می بینید؟ مشاهدۀ اینکه از نقطۀ \((3,15)\) یک خط نرمال به سمت پایین و راست می رود بسیار آسان است، و خط نرمال دیگری رو به پایین و سمت چپ می رود. اما واقعاً آن خط نرمال دومی که رو به سمت پایین و چپ می رود را دیدید؟ اگر آن را ندیدید، نگران نباشید، زیرا هنگامی که عملیات ریاضی را انجام دهید، به هر سه پاسخ می رسید.
انجام برآوردهای مبتنی بر درک عام، فهمیدن ریاضی را تقویت می کند. هنگام انجام حسابان، یا هر ریاضیاتی برای این منظور، به یک برآورد تخمینی مبتنی بر درک عام، برای پاسخ مسأله، قبل از اینکه عملیات ریاضی را انجام دهید، فکر کنید (هرگاه که شدنی باشد و زمان به شما اجازه بدهد). این کار درک شما از مفاهیم گنجانده شده را عمیق تر می کند و همچنین به نوعی یک درست آزمایی برای پاسخ آن مسأله را فراهم می آورد. صرفنظر از این واقعیت که در این مسالۀ خاص، بیشتر افراد حداکثر دو تا از این سه خط را با برآورد چشمی، پیدا می کنند، این یک استراتژی قدرتمند ریاضی است ـــ در این مورد به حرف من اعتماد کنید.
شکل 2-13 این سهمی و این سه خط نرمال را نشان می دهد.

با نگاه کردن به این شکل، شما می توانید از میزان کاربردی بودن این مسأله قدردانی کنید. اگر بر حسب تصادف خودتان را در جایی بیابید که درون یک دیوار سهمی ایستاده باشید، و بخواهید محل دقیق سه نقطه ای بر روی این دیوار را بیابید که می توانید یک توپ را به آنجا پرتاب کنید و مستقیماً به سمت خودتان و رو به عقب باز گردد، در آن صورت این مسأله واقعاً سودمند خواهد بود.
راه حل این مسأله، بسیار شبیه به راه حل مسالۀ خط تانژانت می باشد، با این استثناء که در این مسأله شما از قانون خطهای متعامد (perpendicular lines) استفاده می کنید:
شیب خطهای متعامد (Slopes of perpendicular lines): شیب خطهای متعامد، کسرمتقابل مخالف (opposite reciprocals) یکدیگر می باشند.
یادداشت مترجم: به کسرمتقابل مخالف (opposite reciprocal)، قرینۀ معکوس نیز گفته می شود. اگر دوره های ریاضی را از ابتدا دنبال کرده باشید دلیل اینکه چرا اصرار دارم به جای کلمۀ معکوس از واژۀ "کسر متقابل" برای reciprocal استفاده کنم را خواهید دید.
هر خط نرمال در شکل 2-13 بر خط تانژانتی که در آن نقطه رسم می شود، عمود است. بنابراین شیب هر خط نرمال کسرمتقابل مخالف (قرینۀ معکوس) شیب خط تانژانت متناظرش می باشد ـــ که مسلماً با مشتق بدست می آید. بنابراین راه حل اینگونه خواهد بود:
-
یک نقطۀ عمومی، \((x,y)\)، بر روی این سهمیِ \(y=\frac{1}{16}x^2\) در نظر بگیرید، و \(\frac{1}{16}x^2\) را جایگزین \(y\) کنید.
بنابراین، هر نقطۀ تعامد (point of perpendicularity) را با \(\biggl( x,\frac{1}{16}x^2 \biggr)\) برچسب گذاری کنید.
-
مشتق این سهمی را بدست آورید.
$$y=\frac{1}{16}x^2 \\
y'=\frac{1}{8}x$$
-
با استفاده از فرمول شیب، \(\frac{y_2 - y_1}{x_2-x_1}\)، شیب هر خط نرمال را از \((3,15)\) تا \(\biggl( x,\frac{1}{16}x^2 \biggr)\) برابر با کسرمتقابل مخالف (قرینۀ معکوس) مشتق در \(\biggl( x,\frac{1}{16}x^2 \biggr)\) قرار دهید، و آن را برای بدست آوردن \(x\) حل کنید.
این مشتق برابر با \(\frac{1}{8}x\) یا \(\frac{x}{8}\) می باشد و کسرمتقابل مخالف (قرینۀ معکوس) آن برابر با \(-\frac{8}{x}\) می باشد.
$$\frac{\frac{1}{16}x^2-15}{x-3} = -\frac{8}{x} \\
\frac{1}{16}x^3-15x=-8x+24 \\
x^3-112x-384=0$$
حالا، هیچ راه آسانی برای رسیدن به پاسخهای دقیق این معادلۀ مکعبی (درجۀ سوم)، مانند آنچه که فرمول حل معادلۀ درجه دوم در مورد معادلات درجه دوم به شما می دهد، وجود ندارد. در عوض، شما می توانید نمودار \(y=x^3-112x-384\) را ترسیم کنید، و طول از مبدأها (x-intercepts)، پاسخهای این معادله را به شما می دهند، اما با این روش، هیچ تضمینی وجود ندارد که شما پاسخهای دقیق را بدست آورید. (اگر نتوانستید، برآورد اعشاری بدست آمده کفایت می کند.) البته خوشبختانه در اینجا من پاسخهای دقیق \(-8\)، \(-4\)، و \(12\) را برای شما بدست آورده ام. (شما باید نمودار این تابع مکعبی را بکشید تا بتوانید چگونگی کارکرد آن را ببینید.)
-
هر کدام از این مختصات های \(x\) را در \(y=\frac{1}{16}x^2\) جایگذاری کنید تا مختصات های \(y\) را بدست آورید.
$$\frac{1}{16}(-8)^2=4 \\
\frac{1}{16}(-4)^2=1 \\
\frac{1}{16}(12)^2=9 $$
بدین ترتیب، سه نقطۀ نرمال بودن عبارت از \((-8,4)\)، \((-4,1)\)، و \((12,9))\) می باشند ـــ حالا می توانید آن توپ بازی را که پیشتر اشاره کرده بودم انجام دهید!
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: