جایگزینی های مثلثاتی (Trigonometric Substitution)

با روش جایگزینی مثلثاتی (trigonometric substitution method)، شما می توانید انتگرال هایی شامل رادیکال در این اشکال را انجام دهید: $\sqrt{u^2+a^2}$، $\sqrt{a^2-u^2}$، و $\sqrt{u^2-a^2}$ (و نیز توانهایی از آن ریشه ها)، که در آن $a$ یک ثابت و $u$ عبارتی شامل $x$ می باشد. به عنوان مثال، $\sqrt{3^2-x^2}$ در شکل $\sqrt{a^2-u^2}$ می باشد.

جایگزینی های مثلثاتی (Trigonometric Substitution) شامل سه تابع مثلثاتی می باشند، تانژانت، سینوس، و کسکانت. جدول 1-16 به شما نشان می دهد چگونه این سه تابع با شکل رادیکالشان که در پاراگراف آغازین لیست شد، جفت می شوند.

مورد 1: تانژانت ها (Tangents)

انتگرال زیر را بیابید:
$$\int \frac{dx}{\sqrt{9x^2+4}}$$
ابتدا توجه کنید که این می تواند به شکل زیر بازنویسی گردد:
$$\int \frac{dx}{\sqrt{(3x)^2+2^2}}$$
بنابراین، در شکل $\sqrt{u^2+a^2}$ می گنجد، که در آن $u=3x$ و $a=2$ است؛ شما می توانید ببینید که این با تانژانت در جدول 1-16 جفت می شود.

یک مثلث قائم الزاویه بکشید ـــ در واقع یک مثلث SohCahToa ـــ که در آن $\tan(\theta)$ برابر با $\frac{u}{a}$ باشد، که می شود $\frac{3x}{2}$ .
از آنجا که می دانید $\tan(\theta) = \frac{O}{A}$ است (از روی SohCahToa ـــ فصل 6 را ببینید)، مثلث شما باید دارای $3x$ به عنوان $O$، ضلع روبروی زاویۀ $\theta$ ، و $2$ بعنوان $A$ باشد، ضلع مجاور. سپس، رادیکال شما، یعنی $\sqrt{(3x)^2+2^2}$ یا $\sqrt{9x^2+4}$، به صورت اتوماتیک طول صحیح برای وتر خواهد بود. فکر بدی نیست که این را با قضیۀ فیثاغورث، $a^2+b^2=c^2$، تایید کنیم. شکل 8-16 را ببینید.
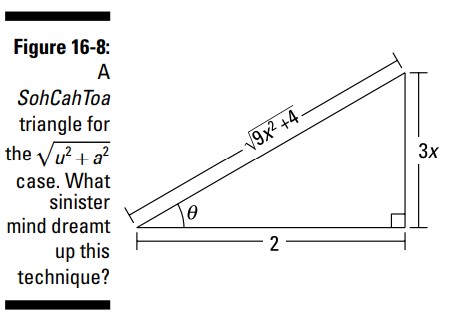
$\tan(\theta)=\frac{3x}{2}$ را برای بدست آوردن $x$ حل کنید، مشتق گیری کنید، و آن را برای بدست آوردن $dx$ حل کنید. $$\frac{3x}{2} = \tan(\theta) \\
3x = 2 \tan(\theta) \\
x= \frac{2}{3} \tan(\theta) \\
\frac{dx}{d\theta}=\frac{2}{3}\sec^2(\theta) \\
dx=\frac{2}{3}\sec^2 (\theta) d\theta$$
پیدا کنید که کدام تابع مثلثاتی با رادیکال بر روی $a$ نشان داده می شود، و آن را برای بدست آوردن رادیکال حل کنید.
به مثلث موجود در شکل 8-16 بنگرید. رادیکال برابر با وتر و $a$ برابر با $2$، ضلع مجاور، می باشد، بنابراین $\frac{\sqrt{9x^2+4}}{2}$ برابر با $\frac{H}{A}$ است، که برابر با سکانت است. بنابراین $\sec(\theta) = \frac{\sqrt{9x^2+4}}{2}$ است، و بدین ترتیب $\sqrt{9x^2+4}=2 \sec(\theta)$ می شود.
از نتایج بدست آمده در مراحل 2 و 3 استفاده کنید تا در مسالۀ اصلی جایگزینی ها را انجام دهید و سپس انتگرال گیری کنید.
از مراحل 2 و 3 نتایج $dx=\frac{2}{3} \sec^2(\theta) d\theta$ و $\sqrt{9x^2+4}=2\sec(\theta)$ را دارید. اکنون در نهایت انتگرال گیری را انجام می دهید.
$$\int \frac{dx}{\sqrt{9x^2+4}} = \int \frac{\frac{2}{3} \sec^2(\theta) d\theta}{2 \sec(\theta)} \\
=\frac{1}{3} \int \sec(\theta) d\theta \\
= \frac{1}{3} \ln |\sec(\theta)+\tan (\theta)| + C$$
(خط آخر انتگرالی هست که شما باید به خاطر بسپارید یا اینکه صرفاً جستجو کنید)
عبارتهای $x$ را از مراحل 1 و 3 در $\sec(\theta)$ و $\tan(\theta)$ جایگذاری کنید. شما همچنین می توانید این عبارتها را از مثلث موجود در شکل 8-16 بگیرید. $$\frac{1}{3} \ln |\frac{\sqrt{9x^2+4}}{2}+\frac{3x}{2}|+C \\
=\frac{1}{3} \ln |\frac{\sqrt{9x^2+4}+3x}{2}|+C \\
=\frac{1}{3} \ln |\sqrt{9x^2+4}+3x|-\frac{1}{3} \ln 2 + C$$
(خط آخر در بالا با استفاده از قانون لگاریتم خارج قسمت و توزیع $\frac{1}{3}$ بدست آمده است)
$$=\frac{1}{3} \ln |\sqrt{9x^2+4}+3x|+C$$
(زیرا $-\frac{1}{3} \ln 2 + C$ صرفاً یک ثابت است)

قبل از اینکه به مقابلۀ مورد 2 برویم، ابتدا چند نکته را بررسی می کنیم.

مورد 1 برابر با $\frac{u}{a}$ می باشد. برای هر سه مورد موجود در جایگزینی مثلثاتی، مرحلۀ 1 همیشه شامل ترسیم یک مثلث است که در آن تابع مثلثاتی در سوال برابر با $\frac{u}{a}$ می باشد:

مورد 1 برابر با $\tan (\theta) = \frac{u}{a}$ است.
مورد 2 برابر با $\sin (\theta) = \frac{u}{a}$ است.
مورد 3 برابر با $\sec (\theta) = \frac{u}{a}$ است.

این واقعیت که این $u$ در صورت کسر $\frac{u}{a}$ قرار می گیرد باید برای یادآوری ساده باشد زیرا $u$ عبارتی دارای $x$ می باشد و چیزی مانند $\frac{3x}{2}$ تاحدی ساده تر و طبیعی تر از دیدن چیزی مانند $\frac{2}{3x}$ است. فقط یادتان باشد که $x$ در بالا قرار می گیرد.

مرحلۀ 3 برابر با $\frac{\sqrt{}}{a}$ است. برای هر سۀ این موارد، مرحلۀ 3 همیشه شامل قرار دادن رادیکال بر روی $a$ می باشد. این سه مورد در زیر آمده اند، اما شما نیازی ندارید تا توابع مثلثاتی این لیست را به حافظه بسپارید زیرا صرفاً با نگاه کردن به این مثلث می دانید که به کدام یکی خواهید رسید ـــ فرض ما بر اینست که با SohCahToa و توابع معکوس مثلثاتی آشنا هستید (اگر نیاز به یادآوری دارید فصل 6 را ببینید). من آن چیزی را که زیر رادیکال قرار می گیرد رها کرده ام زیرا زمانی که مرحلۀ 3 را انجام می دهید، قبلاً به عبارت رادیکال صحیح رسیده اید.

مورد 1 برابر با $\sec (\theta) = \frac{\sqrt{}}{a}$ است.
مورد 2 برابر با $\cos (\theta) = \frac{\sqrt{}}{a}$ است.
مورد 3 برابر با $\tan (\theta) = \frac{\sqrt{}}{a}$ است.

به طور خلاصه، فقط $\frac{u}{a}$ در مرحلۀ 1 و $\frac{\sqrt{}}{a}$ در مرحلۀ 3 یادتان باشد.

مورد 2: سینوس ها (Sines)

انتگرال زیر را بدست آورید:
$$\int \frac{dx}{x^2 \sqrt{16-x^2}}$$
ابتدا آن را به شکل زیر بازنویسی کنید، تا در شکل $\sqrt{a^2-u^2}$ بگنجد، که در آن $a=4$ و $u=x$ است:
$$\int \frac{dx}{x^2 \sqrt{4^2-x^2}}$$

یک مثلث قائم الزاویه بکشید که در آن $\sin (\theta) = \frac{u}{a}$، که برابر با $\frac{x}{4}$ است.
سینوس برابر با $\frac{O}{H}$ است، بنابراین ضلع روبرو برابر با $x$ و وتر برابر با $4$ است. سپس طول ضلع مجاور بصورت اتوماتیک برابر با رادیکال شما، $\sqrt{16-x^2}$ می گردد. (این را با قضیۀ فیثاغورث تایید کنید.) شکل 9-16 را ببینید.
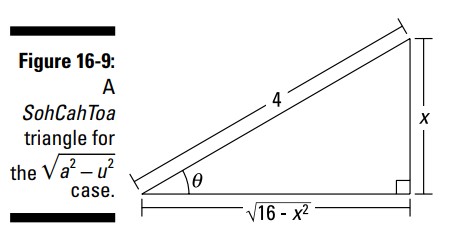
$\sin (\theta) = \frac{x}{4}$ را برای بدست آوردن $x$ حل کنید، مشتق گیری کنید، و آن را برای بدست آوردن $dx$ حل کنید. $$\frac{x}{4} = \sin (\theta) \\
x=4 \sin (\theta)\\
\frac{dx}{d \theta} = 4 \cos (\theta) \\
dx = 4 \cos (\theta) d \theta
$$
پیدا کنید که کدام تابع مثلثاتی برابر با رادیکال بر روی $a$ می باشد، و سپس آن را برای بدست آوردن رادیکال حل کنید.
به مثلث موجود در شکل 9-16 بنگرید. رادیکال، $\sqrt{16-x^2}$، بر روی $a$، $4$، برابر با $\frac{A}{H}$، است که از روی SohCahToa می دانید که برابر با کسینوس است. این به شما نتیجه می دهد:
$$\cos (\theta) = \frac{\sqrt{16-x^2}}{4} \\
\sqrt{16-x^2} = 4 \cos (\theta)$$
از نتایج مراحل 2 و 3 استفاده کنید و جایگزینی ها در مسالۀ اصلی را انجام دهید و سپس انتگرال گیری کنید.
توجه داشته باشید که در اینجا باید سه جایگزینی انجام دهید، و نه مانند مثال اول فقط دو جایگزینی. از مراحل 2 و 3 شما به این نتایج رسیده اید:
$x=4 \sin (\theta)$، $dx=4\cos (\theta) d\theta$، و $\sqrt{16-x^2} = 4 \cos (\theta)$، بنابراین:
$$\int \frac{dx}{x^2 \sqrt{16-x^2}} = \int \frac{4 \cos (\theta) d \theta}{(4 \sin (\theta))^2 4 \cos (\theta)} \\
= \int \frac{d \theta}{16 \sin^2 (\theta)} \\
= \frac{1}{16} \int \csc^2 (\theta) d\theta \\
= - \frac{1}{16} \cot (\theta) + C$$
این مثلث نشان می دهد که $\cot (\theta) = \frac{\sqrt{16-x^2}}{x}$. برای رسیدن به پاسخ نهایی جایگزینی ها را برگردانید. $$=-\frac{1}{16} \cdot \frac{\sqrt{16-x^2}}{x} + C \\
= - \frac{\sqrt{16-x^2}}{16x} + C$$

مورد 3: سکانت ها (Secants)

من می خواهم به خاطر صرفه جویی در زمان از مورد سوم صرفنظر کنم. اما شما با آن هیچ مشکلی نخواهید داشت، زیرا تمامی مراحل آن با موارد 1 و 2 یکسان هستند.

این مورد را امتحان کنید. انتگرال زیر را بدست آورید:
$$\int \frac{\sqrt{x^2-9}}{x} dx$$
در مرحلۀ 1، یک مثلث می کشید، که در آن $\sec (\theta) = \frac{u}{a}$، که $\frac{x}{3}$ است. حالا از آنجا به بعد را پیش ببرید. پاسخ نهایی اینست:
$$\sqrt{x^2-9} - 3 \arctan \biggl( \frac{\sqrt{x^2-9}}{3} \biggr) + C \\
\text{ or } \\
\sqrt{x^2-9} - 3 \text{ arcsec } \biggl( \frac{x}{3} \biggr) + C \\
\text{ or } \\
\sqrt{x^2-9} - 3 \arccos \biggl( \frac{3}{x} \biggr) + C
$$

آموزش قبلی صفحۀ اصلی دوره آموزش بعدی