خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مساحت بین دو منحنی

این اولین موضوع از چندین موضوعی در این فصل است که کار شما یافتن عبارتی برای یک تکۀ کوچک از چیزی می باشد، سپس آن تکه ها را با انتگرال گیری با یکدیگر جمع می زنید. برای این نوع مسالۀ اول، آن تکۀ کوچک یک مستطیل باریک است که بر روی یک منحنی قرار گرفته است و به سمت دیگری بالا می رود. در اینجا مثالی داریم: مساحتی بین \(y=2-x^2\) و \(y=\frac{1}{2}x\) از \(x=0\) تا \(x=1\) را بیابید. شکل 2-17 را ببینید.

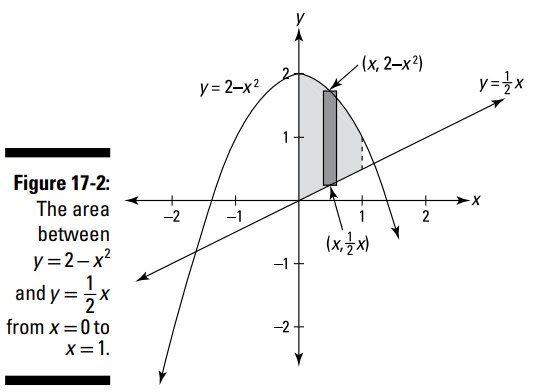
برای بدست آوردن ارتفاع مستطیل نماینده (representative) در شکل 2-17، مختصات \(y\) پایین آن را از مختصات \(y\) بالای آن تفریق کنید ـــ آن \((2-x^2)-\frac{1}{2}x\) می باشد. قاعدۀ آن \(dx\) بی نهایت کوچک می باشد. بنابراین، از آنجا که مساحت برابر با ارتفاع ضربدر قاعده می باشد،
$$\text{Area of representative rectangle}=((2-x^2)-\frac{1}{2}x) dx$$
اکنون شما صرفاً مساحت تمامی این مستطیل ها از \(0\) تا \(1\) را با انتگرال گیری با یکدیگر جمع می کنید:
$$\int_0^1 \bigl( (2-x^2)-\frac{1}{2}x \bigr)dx \\
= \bigl[ 2x-\frac{1}{3}x^3-\frac{1}{4}x^2 \bigr]_0^1 \\ $$
(برای هر سه تکه از قانون توان استفاده شده است)
$$=\bigl( 2-\frac{1}{3}-\frac{1}{4} \bigr) - (0-0-0)\\
=\frac{17}{12} \text{ squre units}$$
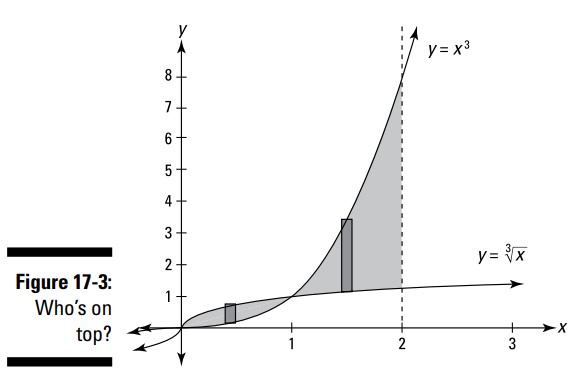
اکنون برای اینکه چیزها را اندکی پیچیده تر کنیم، در مسالۀ بعدی منحنی ها همدیگر را قطع می کنند (شکل 3-17 را ببینید). هنگامی که این اتفاق می افتد، شما باید قبل از انتگرال گیری، مجموع دو مساحت سایه دار شده را به دو ناحیۀ مجزا جدا کنید. این یکی را امتحان کنید: مساحت بین \(\sqrt[3]{x}\) و \(x^3\) را از \(x=0\) تا \(x=2\) بیابید.
اگر در مورد این روش بالا منهای پایین برای محاسبۀ ارتفاع یک مستطیل فکر کنید، خواهید دانست که چرا انتگرال معینِ یک تابع مساحت زیر محور \(x\) را به عنوان منفی در نظر می گیرد. (در فصل 14 و 15 این موضوع را مورد اشاره قرار داده ام.) به عنوان مثال، شکل 4-17 را در نظر بگیرید.
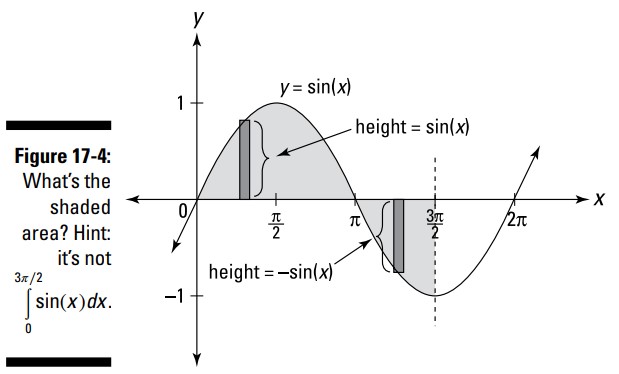
اگر مجموع مساحت ناحیۀ سایه دار شده در شکل 4-17 را بخواهید، باید ناحیۀ سایه دار شده را به دو تکۀ جداگانه تقسیم کنید، مشابه چیزی که در مسالۀ قبلی انجام دادید. یک تکه از \(0\) تا \(\pi\) می رود، و دیگری از \(\pi\) تا \(\frac{3\pi}{2}\) می رود.
برای تکۀ اول، از \(0\) تا \(\pi\)، یک مستطیلِ نماینده، دارای ارتفاعی برابر با خود تابع، \(y=\sin(x)\)، می باشد ـــ و مسلماً هر چیزی منهای صفر برابر با خودش می باشد. بنابراین مساحت این تکۀ اول با انتگرال معین و معمولی \(\int_0^{\pi} \sin(x) dx\) بدست می آید.
اما برای تکۀ دوم از \(\pi\) تا \(\frac{3\pi}{2}\)، بالای مستطیلِ نماینده در صفر قرار دارد ـــ بیاد بیاورید که محور \(x\) خط \(y=0\) می باشد ـــ و پایین آن در \(y=\sin(x)\) می باشد، بنابراین ارتفاع آن برابر با \(0-\sin(x)=-\sin(x)\) می باشد. بنابراین، برای بدست آوردن مساحت این تکۀ دوم، انتگرال معین منفی این تابع را محاسبه می کنید، \(\int_{\pi}^{\frac{3\pi}{2}} (-\sin(x)) dx\)، که با \(- \int_{\pi}^{\frac{3\pi}{2}} \sin(x) dx\) یکسان می باشد.
از آنجا که این انتگرال منفی، مساحت مثبت معمولی این تکۀ زیر محور \(x\) را به شما می دهد، انتگرال معین مثبت \(\int_{\pi}^{\frac{3\pi}{2}} \sin(x)dx\) یک مساحت منفی را می دهد. به همین دلیل است که اگر شما انتگرال معین \(\int_{\pi}^{\frac{3\pi}{2}} \sin(x)dx\) در کل این محدوده را محاسبه کنید، تکۀ زیر محور \(x\) به عنوان مساحت منفی در نظر گرفته می شود، و این پاسخ مساحت خالص بالای محور \(x\) منهای مساحت زیر محور \(x\) را به شما می دهد ـــ به جای مجموع مساحت ناحیۀ سایه دار شده.


برای بدست آوردن ارتفاع مستطیل نماینده (representative) در شکل 2-17، مختصات \(y\) پایین آن را از مختصات \(y\) بالای آن تفریق کنید ـــ آن \((2-x^2)-\frac{1}{2}x\) می باشد. قاعدۀ آن \(dx\) بی نهایت کوچک می باشد. بنابراین، از آنجا که مساحت برابر با ارتفاع ضربدر قاعده می باشد،
$$\text{Area of representative rectangle}=((2-x^2)-\frac{1}{2}x) dx$$
اکنون شما صرفاً مساحت تمامی این مستطیل ها از \(0\) تا \(1\) را با انتگرال گیری با یکدیگر جمع می کنید:
$$\int_0^1 \bigl( (2-x^2)-\frac{1}{2}x \bigr)dx \\
= \bigl[ 2x-\frac{1}{3}x^3-\frac{1}{4}x^2 \bigr]_0^1 \\ $$
(برای هر سه تکه از قانون توان استفاده شده است)
$$=\bigl( 2-\frac{1}{3}-\frac{1}{4} \bigr) - (0-0-0)\\
=\frac{17}{12} \text{ squre units}$$
اکنون برای اینکه چیزها را اندکی پیچیده تر کنیم، در مسالۀ بعدی منحنی ها همدیگر را قطع می کنند (شکل 3-17 را ببینید). هنگامی که این اتفاق می افتد، شما باید قبل از انتگرال گیری، مجموع دو مساحت سایه دار شده را به دو ناحیۀ مجزا جدا کنید. این یکی را امتحان کنید: مساحت بین \(\sqrt[3]{x}\) و \(x^3\) را از \(x=0\) تا \(x=2\) بیابید.

-
تعیین کنید که این دو منحنی در کجا همدیگر را قطع می کنند.
آنها در \((1,1)\) همدیگر را قطع می کنند، بنابراین، شما دو ناحیۀ جداگانه را بدست می آورید: یکی از \(0\) تا \(1\) و دیگری از \(1\) تا \(2\).
-
مساحت ناحیۀ سمت چپ را محاسبه کنید.
برای این ناحیه، \(\sqrt[3]{x}\) بالای \(x^3\) است. بنابراین ارتفاع مستطیل نماینده برابر با \(\sqrt[3]{x}-x^3\)، مساحت آن برابر با ارتفاع آن ضربدر قاعده اش، یا \(\biggl( \sqrt[3]{x}-x^3 \biggr) dx\)، می باشد و بدین ترتیب مساحت این ناحیه،
$$\int_0^1 \biggl( \sqrt[3]{x}-x^3 \biggr) dx \\
=\biggl[ \frac{3}{4}x^{\frac{4}{3}} - \frac{1}{4}x^4 \biggr]_0^1 \\
=\biggl( \frac{3}{4}-\frac{1}{4} \biggr) - (0-0) \\
=\frac{1}{2}$$
-
مساحت ناحیه سمت راست را محاسبه کنید.
در ناحیۀ سمت راست، \(x^3\) بالای \(\sqrt[3]{x}\) است، بنابراین ارتفاع این مستطیل برابر با \(x^3 - \sqrt[3]{x}\) می باشد و از اینرو شما دارید،
$$\int_1^2 \biggl( x^3 - \sqrt[3]{x} \biggr) dx \\
=\biggl[ \frac{1}{4} x^4 - \frac{3}{4}x^{\frac{4}{3}} \biggr]_1^2 \\
=(4-\frac{3}{2} \sqrt[3]{2}) - \biggl( \frac{1}{4}-\frac{3}{4} \biggr) \\
=4.5 - 1.5 \sqrt[3]{2} \\
\approx 2.61$$
-
مساحت های این دو ناحیه را با یکدیگر جمع بزنید تا مجموع مساحت را بدست آورید.
$$0.5+\sim 2.62 \approx 3.11 \text{ square units}$$
ارتفاع برابر با بالا منهای پایین می باشد. توجه داشته باشید که ارتفاع یک مستطیل نماینده همواره برابر با بالای آن منهای پایین آن می باشد، صرفنظر از اینکه این اعداد مثبت یا منفی باشند. به عنوان مثال، مستطیلی که از \(20\) تا \(30\) بالا می رود دارای ارتفاع \(30-20=10\) می باشد؛ مستطیلی که از \(-3\) تا \(8\) بالا می رود، دارای ارتفاع \(8-(-3)=11\) است؛ و مستطیلی که از \(-15\) تا \(-10\) بالا می رود دارای ارتفاع \(-10-(-15)=5\) است.
اگر در مورد این روش بالا منهای پایین برای محاسبۀ ارتفاع یک مستطیل فکر کنید، خواهید دانست که چرا انتگرال معینِ یک تابع مساحت زیر محور \(x\) را به عنوان منفی در نظر می گیرد. (در فصل 14 و 15 این موضوع را مورد اشاره قرار داده ام.) به عنوان مثال، شکل 4-17 را در نظر بگیرید.

اگر مجموع مساحت ناحیۀ سایه دار شده در شکل 4-17 را بخواهید، باید ناحیۀ سایه دار شده را به دو تکۀ جداگانه تقسیم کنید، مشابه چیزی که در مسالۀ قبلی انجام دادید. یک تکه از \(0\) تا \(\pi\) می رود، و دیگری از \(\pi\) تا \(\frac{3\pi}{2}\) می رود.
برای تکۀ اول، از \(0\) تا \(\pi\)، یک مستطیلِ نماینده، دارای ارتفاعی برابر با خود تابع، \(y=\sin(x)\)، می باشد ـــ و مسلماً هر چیزی منهای صفر برابر با خودش می باشد. بنابراین مساحت این تکۀ اول با انتگرال معین و معمولی \(\int_0^{\pi} \sin(x) dx\) بدست می آید.
اما برای تکۀ دوم از \(\pi\) تا \(\frac{3\pi}{2}\)، بالای مستطیلِ نماینده در صفر قرار دارد ـــ بیاد بیاورید که محور \(x\) خط \(y=0\) می باشد ـــ و پایین آن در \(y=\sin(x)\) می باشد، بنابراین ارتفاع آن برابر با \(0-\sin(x)=-\sin(x)\) می باشد. بنابراین، برای بدست آوردن مساحت این تکۀ دوم، انتگرال معین منفی این تابع را محاسبه می کنید، \(\int_{\pi}^{\frac{3\pi}{2}} (-\sin(x)) dx\)، که با \(- \int_{\pi}^{\frac{3\pi}{2}} \sin(x) dx\) یکسان می باشد.
از آنجا که این انتگرال منفی، مساحت مثبت معمولی این تکۀ زیر محور \(x\) را به شما می دهد، انتگرال معین مثبت \(\int_{\pi}^{\frac{3\pi}{2}} \sin(x)dx\) یک مساحت منفی را می دهد. به همین دلیل است که اگر شما انتگرال معین \(\int_{\pi}^{\frac{3\pi}{2}} \sin(x)dx\) در کل این محدوده را محاسبه کنید، تکۀ زیر محور \(x\) به عنوان مساحت منفی در نظر گرفته می شود، و این پاسخ مساحت خالص بالای محور \(x\) منهای مساحت زیر محور \(x\) را به شما می دهد ـــ به جای مجموع مساحت ناحیۀ سایه دار شده.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: