خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
یافتن مساحت یک شکل سه بعدی عجیب

در هندسه آموختید که چگونه حجم های اجسام ساده مانند جعبه ها، استوانه ها، و کره ها را محاسبه کنید. انتگرال گیری شما را قادر می سازد تا حجم های بی نهایت از اجسام متنوع پیچیده تر را محاسبه کنید.

این استعاره در واقع کاملاً صحیح می باشد. یک تکۀ بزرگ گوشت را در نظر بگیرید که با یکی از آن دستگاه های برش گوشت به برش های بسیار باریک بریده شده اند. ایدۀ اصلی اینست، شما یک شکل سه بُعدی را بُرش های زیادی می دهید، سپس حجم آن برش ها را با یکدیگر جمع می زنید تا مجموع حجم را تعیین کنید.
در اینجا مسأله ای داریم: حجم یک شکل سه بعدی که طول آن در امتداد محور \(x\) از \(0\) تا \(\pi\) می رود و سطح مقطع های آن که بر محور \(x\) عمود هستند، مثلث های متساوی الاضلاعی می باشند که نقطۀ میانی قاعده های آنها بر روی محور \(x\) قرار می گیرند و رأس های بالای آنها بر روی منحنی \(y=\sin(x)\) قرار می گیرد؟ توصیف و تصور کردن این مسأله تقریباً از کاری که باید انجام شود سخت تر است. به شکل 5-17 نگاهی بیندازید.
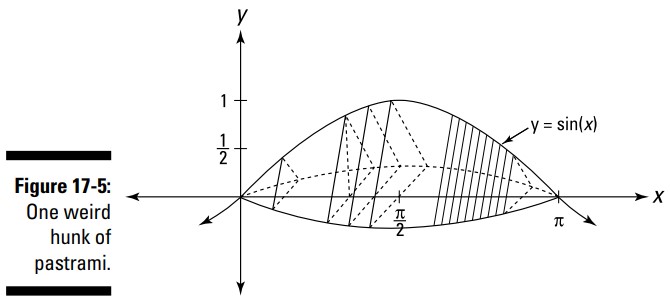
خوب، حجم چقدر است؟
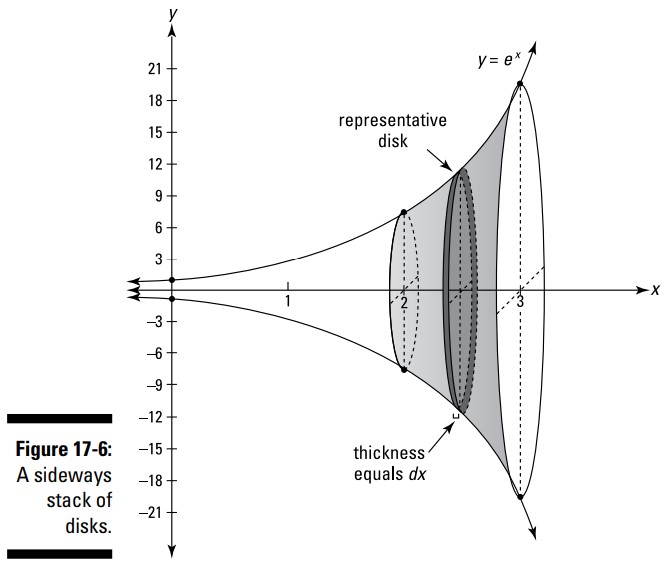
این تکنیک در واقع با روش برش گوشت یکسان است ـــ در واقع یک مورد خاص از روش برش گوشت است که در مواقعی که سطح مقطع ها همگی دایره باشند، مورد استفاده قرار می گیرد. در اینجا چگونگی کارکرد آن را می بینید. حجم شکل سه بعدی زیر را از \(x=2\) تا \(x=3\) بیابید، این شکل با چرخش منحنی \(y=e^x\) در اطراف محور \(x\) تولید شده است. شکل 6-17 را ببینید.

روش بُرش گوشت (meat-slicer method)
این استعاره در واقع کاملاً صحیح می باشد. یک تکۀ بزرگ گوشت را در نظر بگیرید که با یکی از آن دستگاه های برش گوشت به برش های بسیار باریک بریده شده اند. ایدۀ اصلی اینست، شما یک شکل سه بُعدی را بُرش های زیادی می دهید، سپس حجم آن برش ها را با یکدیگر جمع می زنید تا مجموع حجم را تعیین کنید.
در اینجا مسأله ای داریم: حجم یک شکل سه بعدی که طول آن در امتداد محور \(x\) از \(0\) تا \(\pi\) می رود و سطح مقطع های آن که بر محور \(x\) عمود هستند، مثلث های متساوی الاضلاعی می باشند که نقطۀ میانی قاعده های آنها بر روی محور \(x\) قرار می گیرند و رأس های بالای آنها بر روی منحنی \(y=\sin(x)\) قرار می گیرد؟ توصیف و تصور کردن این مسأله تقریباً از کاری که باید انجام شود سخت تر است. به شکل 5-17 نگاهی بیندازید.

خوب، حجم چقدر است؟
-
مساحت هر سطح مقطع ساده را تعیین کنید.
هر سطح مقطع، یک مثلث متساوی الاضلاع با ارتفاع \(\sin(x)\) می باشد. (ارتفاع مثلث دوم از سمت چپ در این شکل نشان داده شده است.) اگر عملیات هندسی را انجام دهید، خواهید دید که قاعدۀ هر مثلث، \(\frac{2\sqrt{3}}{3}\)، ضربدر ارتفاع آن، \(\frac{2\sqrt{3}}{3} \cdot \sin(x)\)، می باشد. (راهنما: نصف یک مثلث متساوی الاضلاع برابر با یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) می باشد.) بنابراین، مساحت این مثلث، با \(A=\frac{1}{2}(b)(h)\) یعنی \(\frac{1}{2} \biggl( \frac{2\sqrt{3}}{3} \cdot \sin(x) \biggr) \sin(x) = \frac{\sqrt{3}}{3}\sin^2(x)\) بدست می آید.
-
حجم یک بُرش نماینده را بیابید.
حجم یک برش صرفاً مساحت سطح مقطع آن ضربدر ضخامت بی نهایت کوچکش، \(dx\)، می باشد. بنابراین شما حجم را دارید:
$$\text{Volume of representative slice } = \frac{\sqrt{3}}{3} \sin^2(x) dx$$
-
با انتگرال گیری حجم های این برش ها را از \(0\) تا \(\pi\) با یکدیگر جمع بزنید.
اگر چیزی که در ادامه آمده است اندکی سخت به نظر می آید، خوب، بهتر است به آن عادت کنید. از این گذشته این حسابان است. (در واقع اگر گام به گام و با صبوری مراحل آن را پیش بروید آنقدرها بد نیست.)
$$
\int_0^x \frac{\sqrt{3}}{3} \sin^2 (x) dx\\
= \frac{\sqrt{3}}{3} \int_0^x \sin^2(x) dx \\
= \frac{\sqrt{3}}{3} \int_0^x \frac{1-\cos(2x)}{2} dx \\
=\frac{\sqrt{3}}{6} \biggl( \int_0^x 1 dx - \int_0^x \cos(2x)dx \biggr) \\
=\frac{\sqrt{3}}{6} \biggl( [x]_0^x - \biggl[ \frac{\sin(2x)}{2} \biggr]_0^x \biggr) \\
= \frac{\sqrt{3}}{6} \biggl( \pi-0- \biggl( \frac{\sin(2x)}{2} - \frac{\sin(0)}{2} \biggr) \biggr)\\
= \frac{\sqrt{3}}{6} \bigl( \pi-0-(0-0) \bigr)\\
=\frac{\pi \sqrt{3}}{6} \\
\approx 0.91 \text{ cubic units}
$$
روش دیسک (disk method)
این تکنیک در واقع با روش برش گوشت یکسان است ـــ در واقع یک مورد خاص از روش برش گوشت است که در مواقعی که سطح مقطع ها همگی دایره باشند، مورد استفاده قرار می گیرد. در اینجا چگونگی کارکرد آن را می بینید. حجم شکل سه بعدی زیر را از \(x=2\) تا \(x=3\) بیابید، این شکل با چرخش منحنی \(y=e^x\) در اطراف محور \(x\) تولید شده است. شکل 6-17 را ببینید.

-
مساحت هر سطح مقطع ساده را تعیین کنید.
هر سطح مقطع دایره ای با شعاع \(e^x\) می باشد. بنابراین، مساحت آن با استفاده از فرمول مساحت دایره، \(A=\pi r^2\)، بدست می آید. با جایگذاری \(e^x\) در \(r\) نتیجۀ زیر را بدست می آورید:
$$A=\pi(e^x)^2=\pi e^{2x}$$
-
\(dx\) را بیفزایید تا حجم یک دیسک نمایندۀ بی نهایت باریک را بدست آورید.
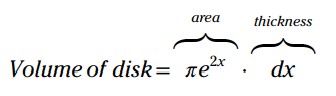
-
حجم های این دیسک ها را از \(2\) تا \(3\) با انتگرال گیری با یکدیگر جمع بزنید.
$$
\text{Total volume}=\int_2^3 \pi e^{2x} dx\\
=\pi \int_2^3 e^{2x} dx\\
=\frac{\pi}{2} \int_2^3 e^{2x} 2dx \\
=\frac{\pi}{2} \int_4^6 e^u du\\
=\frac{\pi}{2} \bigl[ e^u \bigr]_4^6 \\
= \frac{\pi}{2} (e^6 - e^4) \\
\approx 548 \text{ cubic units}
$$
یک دیسک نماینده (representative disk) در مکان خاصی قرار نگرفته است. توجه داشته باشید که مرحلۀ یک به هر سطح مقطع ساده اشاره دارد. من آن را اینگونه نامیده ام زیرا وقتیکه یک دیسک نماینده مانند مورد موجود در شکل 6-17 را در نظر می گیرید، باید بر روی دیسکی تمرکز کنید که در هیچ مکان خاصی قرار ندارد. مورد نشان داده شده در شکل 6-17 در یک مکان نامعلوم بر روی محور \(x\) قرار دارد، و شعاع آن برابر با طول نامعلوم \(e^x\) است. اگر به جای آن از یک دیسک خاص مانند دیسک سمت چپ در \(x=2\) استفاده کنید، به احتمال زیاد این اشتباه را مرتکب می شوید که فکر کنید یک دیسک نماینده دارای شعاع معلومی همچون \(e^2\) است. (این نکته همچنین در مورد روش برش گوشت که پیشتر اشاره شد نیز صدق می کند.)
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: