خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تجزیه و تحلیل طول کمان (Analyzing Arc Length)

تا اینجای این فصل، شما مساحت مستطیل های باریک را با یکدیگر جمع زده اید تا مساحت کل را بدست آورید، و حجم برش های باریک را جمع زده اید تا به حجم کل برسید. اکنون، قصد دارید تا طول های جزئی امتداد یک منحنی (curve) را با یکدیگر جمع بزنید تا به طول کل آن برسید.

من صرفاً می توانم فرمول طول کمان (طول امتداد یک منحنی) را به شما بدهم، اما ترجیح می دهم به شما نشان بدهم چرا آن درست کار می کند و از کجا نتیجه شده است. خوش بحالتان. ایدۀ اصلی اینست که طول یک منحنی را به بخش های کوچک تقسیم کنید، طول هر بخش را بدست آورید، و سپس تمامی این طول ها را با یکدیگر جمع بزنید. شکل 9-17 نشان می دهد چگونه هر بخش از منحنی می تواند با وتر یک مثلث قائم الزاویۀ کوچک تقریب زده شود.
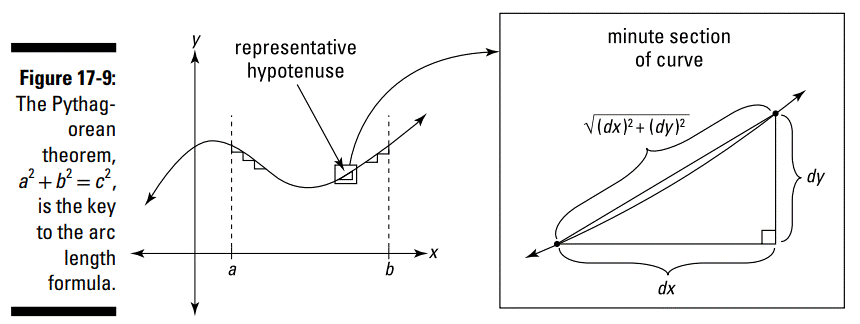
شما می توانید تصور کنید که همینطور که بزرگنمایی را بیشتر و بیشتر می کنید، این منحنی را به بخشهای بیشتر و بیشتری تقسیم می کنید، و بخش های جزئی این منحنی راست تر و راست تر می گردند، و از این رو این وتر کاملاً راست تقریب بهتر و بهتری از این منحنی را می دهد. به همین دلیل هم هست که ـــ هنگامی که این فرآیند جمع زدن بخشهای کوچکتر و کوچکتر به حد برده می شود ـــ شما طول دقیق این منحنی را بدست می آورید.
بنابراین، تمام کاری که شما باید انجام دهید، اینست که تمامی این وترهای موجود در امتداد این منحنی بین نقاط آغازین و پایانی تان را با یکدیگر جمع بزنید. طول ساق های هر کدام از این مثلث های بی نهایت کوچک برابر با \(dx\) و \(dy\) می باشد، و بدین ترتیب طول وتر ـــ که با قضیۀ فیثاغورث بدست می آید ـــ برابر است با:
$$\sqrt{(dx)^2+(dy)^2}$$
برای جمع زدن تمامی این وترهای موجود در امتداد این منحنی از \(a\) تا \(b\)، شما صرفاً انتگرال گیری می کنید:
$$\int_a^b \sqrt{(dx)^2+(dy)^2}$$
اندکی آن را تغییر می دهید و فرمول طول کمان را در اختیار خواهید داشت. ابتدا، \((dx)^2\) را در زیر رادیکال فاکتور بگیرید و سپس ساده سازی کنید:
$$\int_a^b \sqrt{(dx)^2 \biggl[ 1+ \frac{(dy)^2}{(dx)^2} \biggr]} = \int_a^b \sqrt{(dx)^2 \biggl[ 1+ \biggl(\frac{dy}{dx} \biggr)^2 \biggr]}$$
اکنون می توانید جذر \((dx)^2\) را بگیرید و آن را از رادیکال بیرون بکشید، و بالاخره فرمول را دارید ...
این مسأله را امتحان کنید: طول امتداد \(y=(x-1)^{\frac{3}{2}}\) از \(x=1\) تا \(x=5\) چقدر است؟

من صرفاً می توانم فرمول طول کمان (طول امتداد یک منحنی) را به شما بدهم، اما ترجیح می دهم به شما نشان بدهم چرا آن درست کار می کند و از کجا نتیجه شده است. خوش بحالتان. ایدۀ اصلی اینست که طول یک منحنی را به بخش های کوچک تقسیم کنید، طول هر بخش را بدست آورید، و سپس تمامی این طول ها را با یکدیگر جمع بزنید. شکل 9-17 نشان می دهد چگونه هر بخش از منحنی می تواند با وتر یک مثلث قائم الزاویۀ کوچک تقریب زده شود.

شما می توانید تصور کنید که همینطور که بزرگنمایی را بیشتر و بیشتر می کنید، این منحنی را به بخشهای بیشتر و بیشتری تقسیم می کنید، و بخش های جزئی این منحنی راست تر و راست تر می گردند، و از این رو این وتر کاملاً راست تقریب بهتر و بهتری از این منحنی را می دهد. به همین دلیل هم هست که ـــ هنگامی که این فرآیند جمع زدن بخشهای کوچکتر و کوچکتر به حد برده می شود ـــ شما طول دقیق این منحنی را بدست می آورید.
بنابراین، تمام کاری که شما باید انجام دهید، اینست که تمامی این وترهای موجود در امتداد این منحنی بین نقاط آغازین و پایانی تان را با یکدیگر جمع بزنید. طول ساق های هر کدام از این مثلث های بی نهایت کوچک برابر با \(dx\) و \(dy\) می باشد، و بدین ترتیب طول وتر ـــ که با قضیۀ فیثاغورث بدست می آید ـــ برابر است با:
$$\sqrt{(dx)^2+(dy)^2}$$
برای جمع زدن تمامی این وترهای موجود در امتداد این منحنی از \(a\) تا \(b\)، شما صرفاً انتگرال گیری می کنید:
$$\int_a^b \sqrt{(dx)^2+(dy)^2}$$
اندکی آن را تغییر می دهید و فرمول طول کمان را در اختیار خواهید داشت. ابتدا، \((dx)^2\) را در زیر رادیکال فاکتور بگیرید و سپس ساده سازی کنید:
$$\int_a^b \sqrt{(dx)^2 \biggl[ 1+ \frac{(dy)^2}{(dx)^2} \biggr]} = \int_a^b \sqrt{(dx)^2 \biggl[ 1+ \biggl(\frac{dy}{dx} \biggr)^2 \biggr]}$$
اکنون می توانید جذر \((dx)^2\) را بگیرید و آن را از رادیکال بیرون بکشید، و بالاخره فرمول را دارید ...
فرمول طول کمان (Arc length formula): طول کمان در امتداد یک منحنی، \(y=f(x)\)، از \(a\) تا \(b\)، با انتگرال زیر بدست می آید:
$$\int_a^b \sqrt{1+\biggl( \frac{dy}{dx} \biggr)^2}dx$$
عبارت داخل این انتگرال به سادگی طول یک وتر نماینده (representative hypotenuse) می باشد.
$$\int_a^b \sqrt{1+\biggl( \frac{dy}{dx} \biggr)^2}dx$$
عبارت داخل این انتگرال به سادگی طول یک وتر نماینده (representative hypotenuse) می باشد.
این مسأله را امتحان کنید: طول امتداد \(y=(x-1)^{\frac{3}{2}}\) از \(x=1\) تا \(x=5\) چقدر است؟
-
مشتق تابعتان را بدست آورید.
$$y=(x-1)^{\frac{3}{2}}\\
\frac{dy}{dx}=\frac{3}{2}(x-1)^{\frac{1}{2}}$$
-
این مشتق را در فرمول جایگذاری کنید و انتگرال گیری نمایید.
$$\int_a^b \sqrt{1+\biggl( \frac{dy}{dx} \biggr)^2}dx\\
=\int_1^5 \sqrt{1+\biggl( \frac{3}{2}(x-1)^{\frac{1}{2}} \biggr)^2}dx\\
=\int_1^5 \sqrt{1+ \frac{9}{4}(x-1) }dx\\
=\int_1^5 \biggl( \frac{9}{4}x-\frac{5}{4} \biggr)^{\frac{1}{2}} dx\\
=\biggl[ \frac{4}{9} \cdot \frac{2}{3} (\frac{9}{4}x-\frac{5}{4})^{\frac{3}{2}} \biggr]_1^5$$
(ببینید من چطور به آن رسیدم؟ از تکنیک انتگرال گیری با حدس زدن و درست آزمایی همراه با قانون معکوس توان استفاده کرده ام. \(\frac{4}{9}\) مقدار ویرایش شدۀ مورد نیاز است، زیرا ضریب \(\frac{9}{4}\) است.)
$$=\biggl[ \frac{1}{27}(9x-5)^{\frac{3}{2}} \biggr]_1^5 \\
=\frac{1}{27} \biggl( \sqrt{40} \biggr)^3 - \frac{1}{27} \biggl( \sqrt{4} \biggr)^3 \\
=\frac{8}{27} \biggl( (\sqrt{10})^3 -1 \biggr)\\
\approx 9.07 \text{ units}$$
حالا اگر تابحال خودتان را در جاده ای با شکل \(y=(x-1)^{\frac{3}{2}}\) یافتید و کیلومتر شمار شما شکسته شده باشد، شما می توانید طول دقیق مسیر رانندگی تان را محاسبه کنید. دوستان شما بسیار تحت تاثیر قرار خواهند گرفت ـــ یا خیلی نگران خواهند شد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: