در بخش 1.3 واحد اندازه گیری رادیان (radian) و توابع مثلثاتی اصلی (basic trigonometric functions) مورد بررسی قرار می گیرند. زوایا (Angles) در واحد درجه (degrees) یا رادیان (radians) اندازه گیری می شوند. تعداد رادیان ها در زاویۀ مرکزیِ \(A'CB'\) در دایره ای با شعاع \(r\) با تعداد واحدهای شعاع (radius units) که در داخل کمان \(s\) که با آن زاویه جدا شده است، قرار می گیرند، تعریف می شود. اگر این زاویۀ مرکزی را با \(\theta\) نشان دهیم که در واحد رادیان اندازه گیری شده است، بدین معناست که \(\theta = \frac{s}{r}\) (شکل \(\text{1.36}\))، یا:







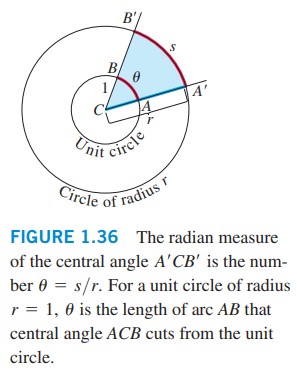
اگر این دایره، یک دایرۀ واحد (unit circle) با شعاع \(r=1\) باشد، آن گاه از روی شکل \(\text{1.36}\) و معادلۀ \((1)\) می بینیم که این زاویۀ مرکزیِ \(\theta\) در واحد رادیان اینگونه اندازه گیری می شود که برابر با طول کمانی است که این زاویه از دایرۀ واحد جدا می کند. از آنجا که یک دوران کامل از دایرۀ واحد برابر با \(360^{\circ}\) یا \(2\pi\) است، خواهیم داشت:


جدول \(\text{1.1}\) معادل های بین درجه و رادیان را برای چند زاویۀ اصلی نشان می دهد.

برای بزرگنمایی تصویر روی آن کلیک کنید
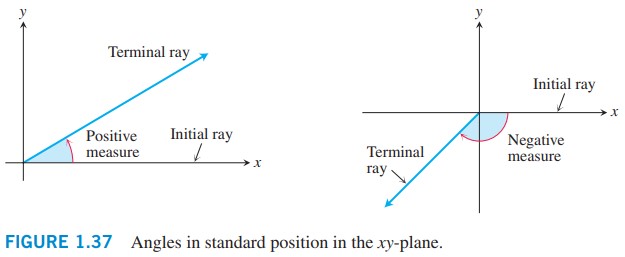
اگر یک زاویه در صفحۀ \(xy\) به نحوی قرار گرفته باشد که رأس (vertex) آن در مبدأ مختصات (origin) باشد و نیم خط آغازین (initial ray) آن در امتداد محور \(x\) مثبت باشد، گفته می شود که در موقعیت استاندارد (standard position) قرار گرفته است (شکل \(\text{1.37}\)). زوایا از محور \(x\) مثبت به صورت پاد ساعت گرد (counterclockwise) به عنوان زوایای مثبت اندازه گیری می شوند؛ همچنین زوایا از همان مکان به صورت ساعت گرد (clockwise) به عنوان زوایای منفی اندازه گیری می گردند.


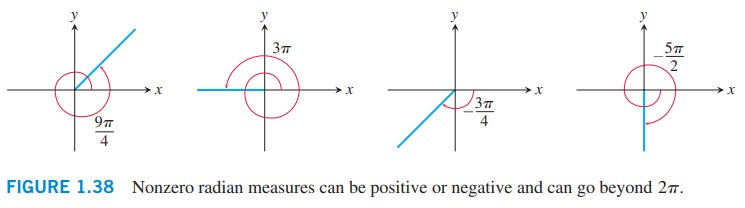
زوایایی که به صورت پادساعت گرد توصیف می شوند می توانند به طور دلخواه دوران هایی فراتر از \(2\pi\) یا \(360^{\circ}\) داشته باشند. به طور مشابهی، زوایایی که به صورت ساعت گرد توصیف می شوند نیز می توانند مقادیر منفی با هر اندازه ای داشته باشند (شکل \(\text{1.38}\)).


قرارداد زاویه: از واحد رادیان استفاده کنید. از این به بعد، در این کتاب فرض می شود که تمامی زوایا در واحد رادیان اندازه گیری می شوند، مگر اینکه واحد اندازه گیری درجه یا سایر واحدهای اندازه گیری صراحتاً اعلام شوند. هنگامی که در مورد زاویۀ \(\frac{\pi}{3}\) صحبت می کنیم، منظورمان \(\frac{\pi}{3}\) رادیان است (که برابر با \(60^{\circ}\) است)، و نه \(\frac{\pi}{3}\) درجه. ما به این دلیل از واحد رادیان استفاده می کنیم که بسیاری از عملیات ها در حسابان را ساده سازی می کند و برخی نتایجی که بدست خواهیم آورد شامل توابع مثلثاتی می باشند که وقتی که آن زوایا را در واحد درجه اندازه گیری کنیم، صحیح نمی باشند.