نویسنده : امیر انصاری

1. $$
   9x^2+12x=-4
   $$
   
2. $$
   5x^2-7x-1=0
   $$
   

پاسخ

1. ابتدا معادلۀ \(9x^2+12x=-4\) را در شکل \(ax^2+bx+c=0\) بنویسید.
   $$
   9x^2+12x+4=0
   $$
   در \(9x^2+12x+4=0\) داریم: \(a=9\)، \(b=12\)، و \(c=4\)
   $$
   x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
   x=\frac{-\color{red}{12} \pm \sqrt{(\color{red}{12})^2-4(\color{red}{9})(\color{red}{4})}}{2(\color{red}{9})}\\
   x=\frac{-12 \pm \sqrt{144-144}}{18}\\
   x=\frac{12 \pm \sqrt{0}}{18}
   $$
   از آنجا که مقدار مبین برابر با صفر می باشد، در این معادله تنها یک ریشۀ حقیقی وجود خواهد داشت یا اینکه دو ریشۀ حقیقی برابر خواهیم داشت.
   $$
   x=\frac{-12}{18}\\
   x=-\frac{2}{3}
   $$
   درست آزمایی پاسخ بدست آمده: \(x=-\frac{2}{3}\) را در معادلۀ اصلی جایگذاری کنید.
   $$
   9x^2+12x=-4\\
   9\bigl( \color{red}{-\frac{2}{3}} \bigr)^2+12\bigl( \color{red}{-\frac{2}{3}} \bigr)=-4\\
   9\bigl( \frac{4}{9} \bigr)-8=-4\\
   9\bigl( \frac{4}{9} \bigr)-8=-4\\
   4-8=-4\\
   -4=-4 \text{ ✔️}
   $$
   ریشه این معادله برابر با \(-\frac{2}{3}\) یا تقریباً \(-0.67\) می باشد.
   
   
2. در \(5x^2-7x-1=0\) داریم: \(a=5\)، \(b=-7\)، و \(c=-1\)
   $$
   x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\\
   x=\frac{-(\color{red}{-7}) \pm \sqrt{(\color{red}{-7})^2-4(\color{red}{5})(\color{red}{-1})}}{2(\color{red}{5})}\\
   x=\frac{7 \pm \sqrt{49+20}}{10}\\
   x=\frac{7 \pm \sqrt{69}}{10}\\
   \text{ }\\[2ex]
   x=\frac{7+\sqrt{69}}{10}\\
   x=1.5306...\\
   x \approx 1.53\\
   \text{ }\\[2ex]
   x=\frac{7-\sqrt{69}}{10}\\
   x=-0.1306...\\
   x \approx -0.13
   $$
   ریشه های این معادله برابر با \(\frac{7+\sqrt{69}}{10}\) و \(\frac{7-\sqrt{69}}{10}\)، یا تقریباً \(1.53\) و \(-0.13\) می باشند.
   
   درست آزمایی: این بار با کمک فناوری ترسیم نمودار، پاسخ های بدست آمده را درست آزمایی می کنیم. نمودار تابع متناظر این معادله، \(y=5x^2-7x-1\) نشان می دهد که صفرهای این تابع تقریباً برابر با \((-0.13.0)\) و \((1.53,0)\) می باشند.
   
   
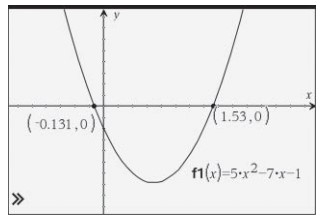
   از این رو مشخص می گردد هر دو پاسخ بدست آمده صحیح می باشند.
   

حالا نوبت شماست

1. $$
   3x^2+5x-2=0
   $$
   
2. $$
   \frac{t^2}{2}-t-\frac{5}{2}=0
   $$