خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
فعالیت 3، تجزیه عبارت های جبری، فصل 4، ریاضی هشتم

برای تجزیۀ یک عبارت جبری، عامل یا بخش مشترک دو یا چند جمله را پیدا می کنیم و بیرون پرانتز می نویسیم. برای تشخیص قسمت مشترک، می توان عبارت ها را به صورت ضرب نوشت:

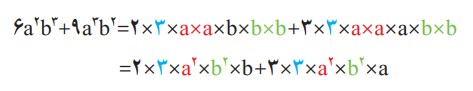
با توجه به تساوی بالا، عامل مشترک دو جملۀ عبارت جبری چیست؟
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ اول عبارت ساخته می شود؟
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ دوم عبارت ساخته می شود؟
حالا این تساوی را کامل کنید.
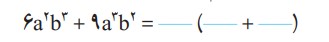
با توجه به تساوی بالا، عامل مشترک دو جملۀ عبارت جبری چیست؟ $$
3a^2b^2
$$
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ اول عبارت ساخته می شود؟ $$
6a^2b^3 = 3a^2b^2 \times 2b
$$
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ دوم عبارت ساخته می شود؟ $$
9a^3b^2 = 3a^2b^2 \times 3a
$$
حالا این تساوی را کامل کنید. $$
6a^2b^3 + 9a^3b^2 = 3a^2b^2( 2b + 3a )
$$

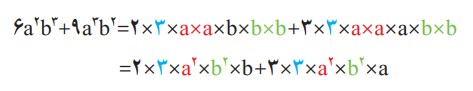
با توجه به تساوی بالا، عامل مشترک دو جملۀ عبارت جبری چیست؟
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ اول عبارت ساخته می شود؟
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ دوم عبارت ساخته می شود؟
حالا این تساوی را کامل کنید.
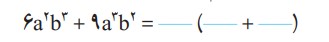
پاسخ
با توجه به تساوی بالا، عامل مشترک دو جملۀ عبارت جبری چیست؟ $$
3a^2b^2
$$
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ اول عبارت ساخته می شود؟ $$
6a^2b^3 = 3a^2b^2 \times 2b
$$
با ضرب کردن چه عبارتی در جملۀ مشترک، جملۀ دوم عبارت ساخته می شود؟ $$
9a^3b^2 = 3a^2b^2 \times 3a
$$
حالا این تساوی را کامل کنید. $$
6a^2b^3 + 9a^3b^2 = 3a^2b^2( 2b + 3a )
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: