خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 9: آزمون تمرینی فصل 8، پاسخ کوتاه

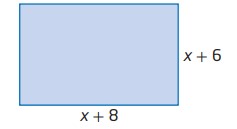
محیط مستطیل با \(8y\) و مساحت آن \((6y + 3)\) می باشد.



-
دو معادله به لحاظ \(x\) و \(y\) بنویسید: یکی برای محیط و دیگری برای مساحت این مستطیل.
-
محیط و مساحت این مستطیل را تعیین کنید.
پاسخ
-
$$
2(x+8) + 2(x+6) = 8y\\
(x+6)(x+8) = 6y + 3
$$
-
برای یافتن محیط و مساحت این مستطیل، ابتدا دستگاه معادلاتی را که در بخش a ایجاد کردیم، حل می کنیم تا مقادیر \(x\) و \(y\) را تعیین کنیم. سپس با داشتن این مقادیر، می توانیم به سادگی محیط و مساحت این مستطیل را تعیین کنیم.
ابتدا معادلات دستگاه را ساده سازی می کنیم تا شکیل تر و شسته رفته تر گردند.
$$
2(x+8) + 2(x+6) = 8y\\
(x+6)(x+8) = 6y + 3\\[2ex]
2(x+8) + 2(x+6) = 8y\\
2x+16 +2x + 12 = 8y\\
4x + 28 = 8y\\[2ex]
(x+6)(x+8) = 6y + 3\\
x^2 + 8x + 6x + 48 = 6y + 3\\
x^2 + 14x + 45 = 6y
$$
بعد از ساده سازی معادلات به دستگاه زیر می رسیم.
$$
4x + 28 = 8y\\
x^2 + 14x + 45 = 6y
$$
با روش حذف این دستگاه را حل می کنیم. معادلۀ اول را در \(-3\) و معادلۀ دوم را در \(4\) ضرب می کنیم تا در هر دو معادله ضریب \(y\) برابر با \(24\) گردد و علامت هایشان نیز متفاوت باشد.
$$
-3(4x + 28) = -3(8y)\\
4(x^2 + 14x + 45) = 4(6y)\\[2ex]
-12x - 84 = -24y\\
4x^2 + 56x + 180 = 24y\\[2ex]
4x^2 + 44x +96 = 0\\
4(x^2 + 11x + 24) = 0\\
4(x+3)(x+8)=0\\
x=-3 \text{ or } x=-8
$$
هم اکنون مقادیر احتمالی \(x\) را داریم، با جایگذاری آن ها در یکی از معادله های اصلی، مقادیر احتمالی \(y\) را بدست می آوریم.
$$
2(x+8) + 2(x+6) = 8y\\
2(\color{red}{-3}+8) + 2(\color{red}{-3}+6) = 8y\\
2(5)+2(3)=8y\\
10 + 6 = 8y\\
16 = 8y\\
2 = y\\
\to (-3,2) \\[2ex]
2(x+8) + 2(x+6) = 8y\\
2(\color{red}{-8}+8) + 2(\color{red}{-8}+6) = 8y\\
2(0) + 2(-2) = 8y\\
-4 = 8y\\
-2 = y\\
\to (-8,-2)
$$
پاسخ های این دستگاه \((-3,2)\) و \((-8,-2)\) می باشند، پاسخ \(-8\) را نادیده می گیریم، چرا که با توجه به محتوای مسئلۀ ما قابل قبول نمی باشد. اگر \(x=-8\) باشد، طول مستطیل ما \(x+8=-8+8=0\) می شود که منطقی نیست. پس \(x=-3\) و \(y=2\) پاسخ مورد نظر ما است.
محیط این مستطیل:
$$
8y = 8(2) = 16
$$
مساحت این مستطیل:
$$
6y+3= 6(2)+3 = 12+3=15
$$
محیط این مستطیل \(16\) متر و مساحت آن \(15\) متر مربع می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: