خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 12: آزمون تمرینی فصل 8، پاسخ طولانی

سهمی \(y = -x^2 + 4x + 26.5\) محور \(x\) را در نقاط \(A\) و \(B\) قطع می کند. خط \(y = 1.5x + 5.25\) این سهمی را در نقاط \(A\) و \(C\) قطع می کند. مساحت تقریبی \(\triangle{ABC}\) را تعیین کنید.

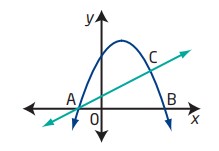
خواستۀ این مسئله مساحت تقریبی مثلث \(ABC\) می باشد. بنابراین مختصات نقاط \(A\) و \(B\) و \(C\) اولین چیزهایی می باشد که باید به دنبالشان باشیم. سپس از روی مختصات این نقاط می توانیم طول \(\overline{AB}\) که قاعدۀ این مثلث می باشد را بدست آوریم. همچنین می توانیم خط فرضی عمودی از نقطۀ \(C\) بر پاره خط \(AB\) در نظر بگیریم که ارتفاع این مثلث می شود. طول این خط برابر با مختصات \(y\) از نقطۀ \(C\) می باشد.
برای بدست آوردن مختصات نقاط \(A\) و \(B\) باید پاسخ های معادلۀ زیر را بیابیم. در واقع این دو نقطه طول از مبدأ های این سهمی می باشند.
$$
-x^2 + 4x + 26.5 = 0
$$
پاسخ های این معادله عبارت از \(A(-3.52,0)\) و \(B(7.52,0)\) می باشند. به کمک این نقاط طول قاعدۀ مثلث را بدست می آوریم.
$$
\overline{AB} = |7.52 - (-3.52)| = 11.04 \\
b = \overline{AB} = 11.04
$$
برای بدست آوردن مختصات نقطۀ \(C\) باید پاسخ های دستگاه معادلات زیر را بیابیم.
$$
y = 1.5x + 5.25\\
y = -x^2 + 4x + 26.5
$$
پاسخ های این دستگاه عبارت از \(A(-3.52,0)\) و \(C(6.02, 14.29)\) می باشند. از روی مختصات \(y\) از نقطۀ \(C\) می توانیم ارتفاع این مثلث را بدست آوریم.
$$
h = 14.29
$$
هم اکنون به سادگی مساحت این مثلث را محاسبه می کنیم.
$$
A = \frac{1}{2} bh\\
A = \frac{1}{2}(11.04)(14.29)\\
A = 78.88
$$
مساحت این مثلث تقریباً \(78.88\) واحد مربع می باشد.


پاسخ
خواستۀ این مسئله مساحت تقریبی مثلث \(ABC\) می باشد. بنابراین مختصات نقاط \(A\) و \(B\) و \(C\) اولین چیزهایی می باشد که باید به دنبالشان باشیم. سپس از روی مختصات این نقاط می توانیم طول \(\overline{AB}\) که قاعدۀ این مثلث می باشد را بدست آوریم. همچنین می توانیم خط فرضی عمودی از نقطۀ \(C\) بر پاره خط \(AB\) در نظر بگیریم که ارتفاع این مثلث می شود. طول این خط برابر با مختصات \(y\) از نقطۀ \(C\) می باشد.
برای بدست آوردن مختصات نقاط \(A\) و \(B\) باید پاسخ های معادلۀ زیر را بیابیم. در واقع این دو نقطه طول از مبدأ های این سهمی می باشند.
$$
-x^2 + 4x + 26.5 = 0
$$
پاسخ های این معادله عبارت از \(A(-3.52,0)\) و \(B(7.52,0)\) می باشند. به کمک این نقاط طول قاعدۀ مثلث را بدست می آوریم.
$$
\overline{AB} = |7.52 - (-3.52)| = 11.04 \\
b = \overline{AB} = 11.04
$$
برای بدست آوردن مختصات نقطۀ \(C\) باید پاسخ های دستگاه معادلات زیر را بیابیم.
$$
y = 1.5x + 5.25\\
y = -x^2 + 4x + 26.5
$$
پاسخ های این دستگاه عبارت از \(A(-3.52,0)\) و \(C(6.02, 14.29)\) می باشند. از روی مختصات \(y\) از نقطۀ \(C\) می توانیم ارتفاع این مثلث را بدست آوریم.
$$
h = 14.29
$$
هم اکنون به سادگی مساحت این مثلث را محاسبه می کنیم.
$$
A = \frac{1}{2} bh\\
A = \frac{1}{2}(11.04)(14.29)\\
A = 78.88
$$
مساحت این مثلث تقریباً \(78.88\) واحد مربع می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: