خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مرتبط ساختن مفاهیم: نامساوی های خطی با دو متغیر

یک نامساوی خطی (linear inequality) با دو متغیر ممکن است در یکی از چهار شکل زیر باشد:

$$
Ax + By \lt C\\
Ax + By \le C\\
Ax + By \gt C\\
Ax + By \ge C
$$
در این نامساوی ها \(A\)، \(B\)، و \(C\) اعداد حقیقی می باشند.
یک نامساوی با دو متغیر \(x\) و \(y\) یک ناحیه در صفحۀ مختصات دکارتی را توصیف می کند. زوج مرتب \((x,y)\) پاسخ یک نامساوی خطی می باشد، اگر آن نامساوی به ازاء مقادیر \(x\) و \(y\) که در آن جایگذاری شده اند، برقرار باشد. مجموعه نقاطی که یک نامساوی خطی را برآورده می سازند می توانند مجموعه پاسخ (solution set) یا ناحیۀ پاسخ (solution region) نامیده شوند.
خط مرتبط با نامساوی خطی \(Ax + By = C\)، یا کرانه (boundary)، صفحۀ مختصات دکارتی را به دو ناحیۀ پاسخ تقسیم می کند.
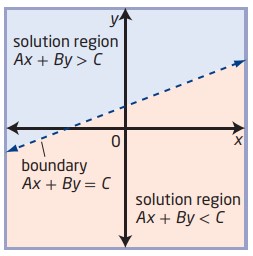
پاسخ یک نامساوی خطی در دو متغیر یک ناحیۀ پاسخ است که ممکن است شامل خط مرزی (کرانه) باشد یا نباشد. این که کرانه بخشی از پاسخ باشد یا نباشد به نامساوی مربوطه بستگی دارد.

$$
Ax + By \lt C\\
Ax + By \le C\\
Ax + By \gt C\\
Ax + By \ge C
$$
در این نامساوی ها \(A\)، \(B\)، و \(C\) اعداد حقیقی می باشند.
یک نامساوی با دو متغیر \(x\) و \(y\) یک ناحیه در صفحۀ مختصات دکارتی را توصیف می کند. زوج مرتب \((x,y)\) پاسخ یک نامساوی خطی می باشد، اگر آن نامساوی به ازاء مقادیر \(x\) و \(y\) که در آن جایگذاری شده اند، برقرار باشد. مجموعه نقاطی که یک نامساوی خطی را برآورده می سازند می توانند مجموعه پاسخ (solution set) یا ناحیۀ پاسخ (solution region) نامیده شوند.
ناحیۀ پاسخ (solution region):
-
تمامی نقاط موجود بر روی صفحۀ مختصات دکارتی که یک نامساوی را برآورده می سازند.
-
همچنین با نام مجموعه پاسخ نیز شناخته می شود.
خط مرتبط با نامساوی خطی \(Ax + By = C\)، یا کرانه (boundary)، صفحۀ مختصات دکارتی را به دو ناحیۀ پاسخ تقسیم می کند.
-
برای یک ناحیۀ پاسخ \(Ax + By \gt C\) برقرار است.
-
برای یک ناحیۀ پاسخ \(Ax + By \lt C\) برقرار است.

کرانه (boundary):
-
یک خط یا یک منحنی که صفحۀ مختصات دکارتی را به دو ناحیه تقسیم می کند.
-
کرانه ممکن است بخشی از ناحیۀ پاسخ باشد یا نباشد.
-
اگر نامساوی مربوطه شامل \(\le\) یا \(\ge\) باشد، کرانه به شکل یک خط توپر (solid line) ترسیم می شود و بخشی از ناحیۀ پاسخ می باشد.
-
اگر نامساوی مربوطه شامل \(\lt\) یا \(\gt\) باشد، کرانه به شکل یک خط چین (dashed line) ترسیم می شود و بخشی از ناحیۀ پاسخ نمی باشد.
پاسخ یک نامساوی خطی در دو متغیر یک ناحیۀ پاسخ است که ممکن است شامل خط مرزی (کرانه) باشد یا نباشد. این که کرانه بخشی از پاسخ باشد یا نباشد به نامساوی مربوطه بستگی دارد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: