خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 4: نامساوی های درجه دوم با یک متغیر، تمرین

از ریشه ها و نقاط آزمایش برای تعیین پاسخ های هر نامساوی استفاده کنید.

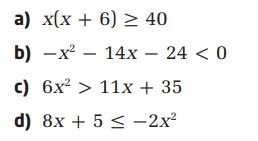
با توجه به مشابه بودن این چهار مورد، گزینۀ a را به صورت تفصیلی پاسخ می دهیم و در سایر موارد به پاسخ کوتاه بسنده می کنیم.

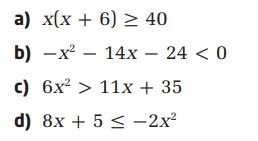
پاسخ
با توجه به مشابه بودن این چهار مورد، گزینۀ a را به صورت تفصیلی پاسخ می دهیم و در سایر موارد به پاسخ کوتاه بسنده می کنیم.
-
ابتدا ریشه های معادلۀ مربوطه را تعیین می کنیم.
$$
x(x+6)=40\\
x^2 + 6x -40 = 0\\
(x+10)(x-4)=0\\[2ex]
x+10=0\\
x=-10\\[2ex]
x-4=0\\
x=4
$$
هم اکنون ریشه ها، یعنی نقاط \(-10\) و \(4\)، را روی یک خط اعداد ترسیم می کنیم. با توجه به اینکه علامت این نامساوی \(\ge\) می باشد، از نقاط توپر برای نشان دادن محل ریشه ها بر روی خط اعداد استفاده می کنیم، چون خود این دو عدد نیز بخشی از پاسخ می باشند.
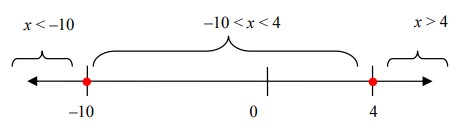
هم اکنون در هر کدام از بازه های مشخص شده بر روی خط اعداد، یک نقطۀ آزمایش انتخاب می کنیم و بررسی می کنیم که به ازاء آن نقطۀ آزمایش، نامساوی برقرار باشد.
بازه \(x \lt -10\)
\(-10 \lt x \lt 4\)
\(x \gt 4\)
نقطۀ آزمایش \(-12\)
\(0\)
\(5\)
جایگذاری $$
\color{red}{-12}(\color{red}{-12}+6)\\
=-12(-6)\\
=72
$$
$$
\color{red}{0}(\color{red}{0}+6)\\
=0
$$
$$
\color{red}{5}(\color{red}{5}+6)\\
=5(11)\\
=55
$$
آیا \(x(x+6) \ge 40\) برقرار است؟
بله
خیر
بله
مجموعه پاسخ این نامساوی به شرح زیر است:
$$
\{ x | x \le -10 \text{ or } x \ge 4 , x \in R \}
$$
-
$$
\{ x | x \lt -12 \text{ or } x \gt -2, x \in R \}
$$
-
$$
\{ x | x \lt -\frac{5}{3} \text{ or } x \gt \frac{7}{2}, x \in R \}
$$
-
$$
\{ x | -2 - \frac{\sqrt{6}}{2} \le x \le -2 + \frac{\sqrt{6}}{2} , x \in R \}
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: