خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 6: نامساوی های درجه دوم با یک متغیر، تمرین

از تجزیه و تحلیل موردی برای تعیین پاسخ نامساوی های زیر استفاده کنید.

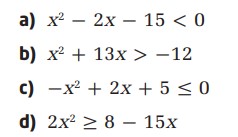
با توجه به یکسان بودن روش حل، گزینۀ a را به صورت تشریحی حل می کنیم و در سایر موارد به پاسخ کوتاه بسنده می کنیم. البته در گزینۀ c به دلیل اینکه قابل فاکتورگیری نمی باشد، اندکی توضیحات بیشتر ارائه می دهیم.

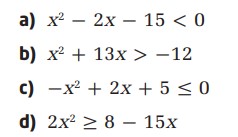
پاسخ
با توجه به یکسان بودن روش حل، گزینۀ a را به صورت تشریحی حل می کنیم و در سایر موارد به پاسخ کوتاه بسنده می کنیم. البته در گزینۀ c به دلیل اینکه قابل فاکتورگیری نمی باشد، اندکی توضیحات بیشتر ارائه می دهیم.
-
ابتدا عبارت درجه دوم را فاکتورگیری می کنیم:
$$
x^2 - 2x - 15 \lt 0\\
(x+3)(x-5) \lt 0
$$
اگر این دو فاکتور دارای علامت های متفاوتی باشند، حاصل ضرب آن ها عددی منفی می شود. برای این که چنین شود، دو حالت خواهیم داشت. در حالت اول، فاکتور اول مثبت و فاکتور دوم منفی خواهد بود. در حالت دوم فاکتور اول منفی و فاکتور دوم مثبت خواهد بود. هر دوی این حالات را تجزیه و تحلیل می کنیم.
حالت اول: فاکتور اول مثبت و فاکتور دوم منفی:
$$
x - 5 \gt 0 \\
x \gt 5\\[2ex]
x + 3 \lt 0 \\
x \lt -3
$$
تجمیع این دو شرط با یکدیگر هرگز برقرار نخواهد بود. به زبان ساده تر ما هیچ مجموعه عدد حقیقی نداریم که بزرگتر از \(5\) و در عین حال کوچکتر از \(-3\) باشند. اگر نتایج را بر روی خط اعداد ترسیم کنید، به صورت تصویری نیز این موضوع را خواهید دید.
حالت دوم: فاکتور اول منفی و فاکتور دوم مثبت:
$$
x-5 \lt 0\\
x \lt 5\\[2ex]
x +3 \gt 0\\
x \gt -3
$$
این دو نامساوی به ازاء تمامی نقاط بین \(-3\) و \(5\) برقرار می باشند.
مجموعه پاسخ این نامساوی: با توجه به تجزیه و تحلیل موردی مشخص می شود که مجموعه پاسخ این نامساوی به شرح زیر می باشد:
$$
\{ x | -3 \lt x \lt 5 , x \in R \}
$$
-
$$
\{ x | x \lt -12 \text{ or } x \gt -1 , x \in R \}
$$
-
ابتدا علامت منفی را فاکتور می گیریم، این کار باعث می شود که علامت نامساوی تغییر کند.
$$
-x^2 + 2x + 5 \le 0\\
x^2 -2x -5 \ge 0
$$
این معادله را با فرمول حل معادلۀ درجه دوم حل می کنیم، چرا که قابل فاکتورگیری نمی باشد.
$$
x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\\
x = \frac{2 \pm \sqrt{24}}{2}\\
x = 1 \pm \sqrt{6}
$$
بنابراین مشخص می شود که این نامساوی دو فاکتور زیر را دارد:
$$
(x-1-\sqrt{6})(x-1+\sqrt{6}) \ge 0
$$
دو حالت این نامساوی بدین شکل هستند که یا هر دو فاکتور باید مثبت باشند و یا هر دو فاکتور باید منفی باشند.
$$
\{ x | x \le 1 - \sqrt{6} \text{ or } x \ge 1 + \sqrt{6}, x \in R \}
$$
-
$$
\{ x | x \le -8 \text{ or } x \ge \frac{1}{2} , x \in R \}
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: