نویسنده : امیر انصاری

1. $$
   -2 \le x \le 7
   $$
   
2. $$
   x \lt 1 \text{ or } x \gt 10
   $$
   
3. $$
   \frac{5}{3} \le x \le 6
   $$
   
4. $$
   x \lt -\frac{3}{4} \text{ or } x \gt -\frac{1}{5}
   $$
   
5. $$
   x \le -3 - \sqrt{7} \text{ or } x \ge -3 + \sqrt{7}
   $$
   
6. $$
   x \in R
   $$
   
7. بدون پاسخ
   

پاسخ

1. تصویر زیر پاسخ این نامساوی را به صورت گرافیکی نشان می دهد. \(-2 \le x \le 7\)
   برای بزرگنمایی تصویر روی آن کلیک کنید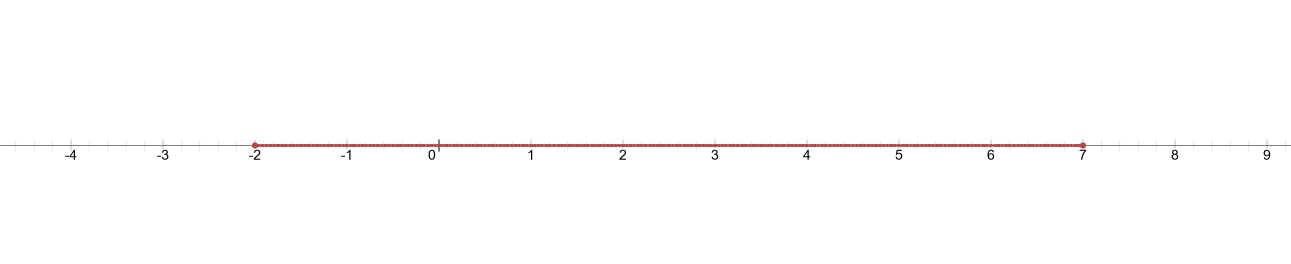
   اگر پاسخ را به شکل تفکیک شده تجزیه و تحلیل کنیم، به ریشه های یک نامساوی درجه دوم می رسیم که در واقع بخشی از پاسخ مسئلۀ ما می باشد.
   $$
   -2 \le x\\
   x \ge -2\\
   x +2 \ge 0
   $$
   $$
   x \le 7\\
   x -7 \le 0
   $$
   $$
   (x+2)(x-7)
   $$
   تا اینجای کار، معادلۀ درجه دومی که بخشی از نامساوی ما می باشد، بدست آمده است. حالا باید بررسی کنیم و علامت این نامساوی را بیابیم. در واقع پاسخ ما می تواند یکی از دو گزینۀ زیر باشد:
   $$
   (x+2)(x-7) \ge 0\\
   \text{ یا } \\
   (x+2)(x-7) \le 0
   $$
   حالا هر کدام از این نامساوی ها را به صورت جداگانه حل می کنیم و پاسخ بدست آمده را با پاسخ اولیه که به ما داده شده است مقایسه می کنیم:
   $$
   (x+2)(x-7) \ge 0\\
   \{ x | x \le -2 \text{ or } x \ge 7 , x \in R \} \text{ ❌}
   $$
   همانطور که می بینید، نامساوی اول ما را به پاسخ صحیح نرساند. نامساوی بعدی را حل کرده و مقایسه می کنیم:
   $$
   (x+2)(x-7) \le 0\\
   \{ x | -2 \le x \le 7, x \in R \} \text{ ✔️}
   $$
   پاسخ صحیح \((x+2)(x-7) \le 0\) می باشد که می توانیم با ضرب دوجمله ای ها در یکدیگر، آن را به شکل بسط یافته اش نیز بنویسیم.
   $$
   (x+2)(x-7) \le 0\\
   x^2 -5x -14 \le 0
   $$
   
2. $$
   (x-1)(x-10) \gt 0\\
   x^2 -11x +10x \gt 0
   $$
   
3. $$
   (3x-5)(x-6) \le 0\\
   3x^2 - 23x + 30 \le 0
   $$
   
4. $$
   (4x+3)(5x+1) \gt 0\\
   20x^2 + 19x + 3 \gt 0
   $$
   
5. $$
   (x+3+\sqrt{7})(x+3-\sqrt{7}) \ge 0 \\
   x^2 +6x +2 \ge 0
   $$
   
6. هر سهمی مثبت که رأس آن بالای محور \(x\) قرار داشته باشد، می تواند به عنوان این نامساوی در نظر گرفته شود. برای مثال:
   $$
   x^2 + 1 \gt 0
   $$
   
7. اگر نامساوی ما یک سهمی باشد که رو به بالا باز شود، و همۀ مقادیر آن مثبت باشند، طبیعتاً هرگز پاسخ حقیقی منفی نخواهد داشت. به عنوان مثال:
   $$
   x^2 + 1 \lt 0
   $$