خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
دامنه و برد توابع

دمای جوشیدن آب به ارتفاع از سطح دریا بستگی دارد (هر چقدر این ارتفاع افزایش یابد، نقطۀ جوش آب کاهش خواهد یافت). سودی که بابت یک سرمایه گذاری پرداخت می شود، به مدت زمان نگهداری آن سرمایه بستگی دارد. مساحت یک دایره به شعاع آن بستگی دارد. مسافت طی شده توسط یک شیء با سرعت ثابت، در امتداد یک مسیر مستقیم، به زمان سپری شده بستگی دارد.

در هر کدام از این موارد، مقدار یک کمیت متغیر که در اینجا آن را \(y\) می نامیم، به مقدار کمیت متغیر دیگری بستگی دارد که معمولاً آن را \(x\) می نامیم و به صورت خلاصه می گوییم که \(y\) تابعی از \(x\) می باشد. این موضوع را به شکل نمادین زیر می نویسیم:
$$
y=f(x)
$$
در این نشانه گذاری، نماد \(f\) نشان دهندۀ تابع، حرف \(x\) نشان دهندۀ متغیر مستقلی است که مقدار ورودی تابع \(f\) می باشد، و \(y\) متغیر وابسته است که مقدار خروجی تابع \(f\) به ازاء ورودی \(x\) می باشد.
مجموعۀ \(D\)، شامل تمامی ورودی های امکان پذیر یک تابع می باشند و دامنۀ این تابع نام دارد. مجموعۀ تمامی مقادیر خروجی این تابع، بُرد این تابع نام دارد. برد ممکن است شامل تمامی عناصر موجود در مجموعۀ \(Y\) نباشد. دامنه و برد یک تابع می توانند شامل هر مجموعه ای از اشیاء باشند، اما در حسابان آنها اغلب مجموعه ای از اعداد حقیقی می باشند که به عنوان نقاطی بر روی یک خط مختصات تفسیر می شوند. (در فصل های \(13\) تا \(16\) با توابعی مواجه خواهیم شد که عناصر آنها مجموعه ای از نقاط در صفحۀ مختصات یا در فضا می باشند.)
معمولاً هر تابع با یک فرمول همراه می گردد که چگونگی محاسبۀ مقدار خروجی از مقدار متغیر ورودی را توصیف می کند. به عنوان مثال، معادلۀ \(A = \pi r^2\) یک قانون است که مساحت یک دایره، \(A\)، را از روی شعاع آن، \(r\)، محاسبه می کند. در اینجا شعاع یعنی \(r\) یک طول می باشد و طبیعتاً فقط می تواند شامل اعداد مثبت باشد. هنگامی که تابع \(y=f(x)\) را با فرمولی تعریف می کنیم که دامنۀ آن صراحتاً بیان نمی شود یا از روی محتوای آن محدود نمی گردد، دامنۀ آن تابع شامل بزرگترین مجموعۀ اعداد حقیقی خواهد بود که به ازاء آنها فرمول تابع می تواند مقادیر حقیقی برای \(y\) تولید کند. به این دامنه، دامنۀ طبیعی گفته می شود. اگر به هر نحوی بخواهیم این دامنه را محدود کنیم، باید صراحتاً بیان کنیم. دامنۀ تابع \(y = x^2\) شامل تمامی اعداد حقیقی می باشد. اگر بخواهیم دامنۀ این تابع را به اعداد مثبت محدود کنیم، آن را به شکل زیر می نویسیم:
$$
y = x^2, x \gt 0
$$
معمولاً تغییر دادن دامنه منجر به تغییر برد تابع نیز می شود. به عنوان مثال برد تابع \(y=x^2, x \gt 0\) برابر با \([0, \infty)\) می باشد. برد تابع \(y=x^2, x \ge 2\)، شامل مجموعۀ تمامی اعدادی می باشد که با مربع ساختن اعداد برابر یا بزرگتر از \(2\) ایجاد می گردند. در نشانه گذاری های مجموعه ها آن را به شکل های زیر نشان می دهند:
$$
\{ x^2 | x \ge 2 \} \\
\{ y | y \ge 4 \} \\
[4, \infty)
$$
هنگامی که برد یک تابع شامل یک مجموعه از اعداد حقیقی باشد، گفته می شود که آن تابع، یک تابع حقیقی می باشد. دامنه و برد بیشتر توابع حقیقی، شامل بازه ها یا ترکیبی از بازه ها می باشند. این بازه ها می توانند باز، بسته، یا نیمه باز باشند. همچنین می توانند متناهی یا نامتناهی باشند. گاهی اوقات یافتن برد یک تابع آسان نمی باشد.
تابع را می توانید مانند یک دستگاه در نظر بگیرید که به ازاء هر مقدار که در دامنۀ آن باشد، مقداری را تولید می کند که در برد آن قرار دارد (شکل \(\text{1.1}\)). دکمه های ماشین حساب مثالی از یک تابع می باشند. به عنوان مثال، دکمۀ \(\sqrt{x}\) بر روی ماشین حساب به ازاء هر مقدار ورودی غیرمنفی، یک مقدار خروجی که ریشۀ دوم (جذر) آن عدد می باشد، تولید می کند.

همچنین می توان تابع را به شکل یک نمودار پیکانی متصور شد (شکل \(\text{1.2}\)). هر پیکان یک عنصر از دامنۀ \(D\) را با یک عنصر یکتا در مجموعۀ \(Y\) مرتبط می سازد. در شکل \(\text{1.2}\) پیکان ها مشخص می سازند که \(f(a)\) به \(a\) مرتبط است، \(f(x)\) با \(x\) مرتبط است، و به همین ترتیب. همچنین توجه داشته باشید که یک تابع می تواند به ازاء دو یا چند ورودی جداگانه، خروجی یکسانی تولید کند، اگر در شکل دقت کنید در مورد خروجی \(f(a)\) این اتفاق رخ داده است و دو ورودی جدا منجر به خروجی یکسانی شده اند. اما توجه داشته باشید که هر ورودی فقط و فقط می تواند یک خروجی داشته باشد و نباید بیش از یک خروجی داشته باشد. در شکل هم مشخص است که هر عنصر از مجموعۀ \(D\) فقط و فقط با یک عنصر در مجموعۀ \(Y\) مرتبط است.

در هر کدام از این موارد، مقدار یک کمیت متغیر که در اینجا آن را \(y\) می نامیم، به مقدار کمیت متغیر دیگری بستگی دارد که معمولاً آن را \(x\) می نامیم و به صورت خلاصه می گوییم که \(y\) تابعی از \(x\) می باشد. این موضوع را به شکل نمادین زیر می نویسیم:
$$
y=f(x)
$$
در این نشانه گذاری، نماد \(f\) نشان دهندۀ تابع، حرف \(x\) نشان دهندۀ متغیر مستقلی است که مقدار ورودی تابع \(f\) می باشد، و \(y\) متغیر وابسته است که مقدار خروجی تابع \(f\) به ازاء ورودی \(x\) می باشد.
تعریف تابع: تابع یک قانون است که هر عنصر در مجموعۀ اول را دقیقاً به یک عنصر در مجموعۀ دوم مرتبط می سازد.
اگر تابع را با \(f\)، مجموعۀ ورودی تابع را با \(D\) و مجموعۀ خروجی آن را با \(Y\) نشان دهیم، خواهیم داشت:
$$
f(x) \in Y\\
x \in D
$$
اگر تابع را با \(f\)، مجموعۀ ورودی تابع را با \(D\) و مجموعۀ خروجی آن را با \(Y\) نشان دهیم، خواهیم داشت:
$$
f(x) \in Y\\
x \in D
$$
مجموعۀ \(D\)، شامل تمامی ورودی های امکان پذیر یک تابع می باشند و دامنۀ این تابع نام دارد. مجموعۀ تمامی مقادیر خروجی این تابع، بُرد این تابع نام دارد. برد ممکن است شامل تمامی عناصر موجود در مجموعۀ \(Y\) نباشد. دامنه و برد یک تابع می توانند شامل هر مجموعه ای از اشیاء باشند، اما در حسابان آنها اغلب مجموعه ای از اعداد حقیقی می باشند که به عنوان نقاطی بر روی یک خط مختصات تفسیر می شوند. (در فصل های \(13\) تا \(16\) با توابعی مواجه خواهیم شد که عناصر آنها مجموعه ای از نقاط در صفحۀ مختصات یا در فضا می باشند.)
معمولاً هر تابع با یک فرمول همراه می گردد که چگونگی محاسبۀ مقدار خروجی از مقدار متغیر ورودی را توصیف می کند. به عنوان مثال، معادلۀ \(A = \pi r^2\) یک قانون است که مساحت یک دایره، \(A\)، را از روی شعاع آن، \(r\)، محاسبه می کند. در اینجا شعاع یعنی \(r\) یک طول می باشد و طبیعتاً فقط می تواند شامل اعداد مثبت باشد. هنگامی که تابع \(y=f(x)\) را با فرمولی تعریف می کنیم که دامنۀ آن صراحتاً بیان نمی شود یا از روی محتوای آن محدود نمی گردد، دامنۀ آن تابع شامل بزرگترین مجموعۀ اعداد حقیقی خواهد بود که به ازاء آنها فرمول تابع می تواند مقادیر حقیقی برای \(y\) تولید کند. به این دامنه، دامنۀ طبیعی گفته می شود. اگر به هر نحوی بخواهیم این دامنه را محدود کنیم، باید صراحتاً بیان کنیم. دامنۀ تابع \(y = x^2\) شامل تمامی اعداد حقیقی می باشد. اگر بخواهیم دامنۀ این تابع را به اعداد مثبت محدود کنیم، آن را به شکل زیر می نویسیم:
$$
y = x^2, x \gt 0
$$
معمولاً تغییر دادن دامنه منجر به تغییر برد تابع نیز می شود. به عنوان مثال برد تابع \(y=x^2, x \gt 0\) برابر با \([0, \infty)\) می باشد. برد تابع \(y=x^2, x \ge 2\)، شامل مجموعۀ تمامی اعدادی می باشد که با مربع ساختن اعداد برابر یا بزرگتر از \(2\) ایجاد می گردند. در نشانه گذاری های مجموعه ها آن را به شکل های زیر نشان می دهند:
$$
\{ x^2 | x \ge 2 \} \\
\{ y | y \ge 4 \} \\
[4, \infty)
$$
هنگامی که برد یک تابع شامل یک مجموعه از اعداد حقیقی باشد، گفته می شود که آن تابع، یک تابع حقیقی می باشد. دامنه و برد بیشتر توابع حقیقی، شامل بازه ها یا ترکیبی از بازه ها می باشند. این بازه ها می توانند باز، بسته، یا نیمه باز باشند. همچنین می توانند متناهی یا نامتناهی باشند. گاهی اوقات یافتن برد یک تابع آسان نمی باشد.
تابع را می توانید مانند یک دستگاه در نظر بگیرید که به ازاء هر مقدار که در دامنۀ آن باشد، مقداری را تولید می کند که در برد آن قرار دارد (شکل \(\text{1.1}\)). دکمه های ماشین حساب مثالی از یک تابع می باشند. به عنوان مثال، دکمۀ \(\sqrt{x}\) بر روی ماشین حساب به ازاء هر مقدار ورودی غیرمنفی، یک مقدار خروجی که ریشۀ دوم (جذر) آن عدد می باشد، تولید می کند.

ترجمۀ شکل:
\(\text{Input}\): ورودی
\(\text{Output}\): خروجی
\(\text{domain}\): دامنه
\(\text{range}\): برد
شکل \(\text{1.1}\): این طرح یک تابع را به شکل یک نوع دستگاه نشان می دهد.
\(\text{Input}\): ورودی
\(\text{Output}\): خروجی
\(\text{domain}\): دامنه
\(\text{range}\): برد
شکل \(\text{1.1}\): این طرح یک تابع را به شکل یک نوع دستگاه نشان می دهد.
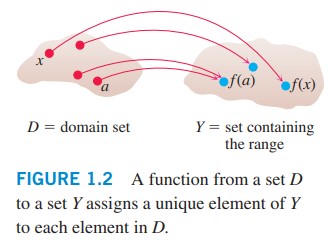
همچنین می توان تابع را به شکل یک نمودار پیکانی متصور شد (شکل \(\text{1.2}\)). هر پیکان یک عنصر از دامنۀ \(D\) را با یک عنصر یکتا در مجموعۀ \(Y\) مرتبط می سازد. در شکل \(\text{1.2}\) پیکان ها مشخص می سازند که \(f(a)\) به \(a\) مرتبط است، \(f(x)\) با \(x\) مرتبط است، و به همین ترتیب. همچنین توجه داشته باشید که یک تابع می تواند به ازاء دو یا چند ورودی جداگانه، خروجی یکسانی تولید کند، اگر در شکل دقت کنید در مورد خروجی \(f(a)\) این اتفاق رخ داده است و دو ورودی جدا منجر به خروجی یکسانی شده اند. اما توجه داشته باشید که هر ورودی فقط و فقط می تواند یک خروجی داشته باشد و نباید بیش از یک خروجی داشته باشد. در شکل هم مشخص است که هر عنصر از مجموعۀ \(D\) فقط و فقط با یک عنصر در مجموعۀ \(Y\) مرتبط است.

ترجمۀ شکل:
\(\text{domain set}\): مجموعۀ دامنه
\(\text{set containing the range}\): مجموعۀ شامل برد
شکل \(\text{1.2}\): یک تابع از مجموعۀ \(D\) به مجموعۀ \(Y\)، یک عنصر یکتا از مجموعۀ \(Y\) را به هر عنصر از مجموعۀ \(D\) مرتبط می سازد.
\(\text{domain set}\): مجموعۀ دامنه
\(\text{set containing the range}\): مجموعۀ شامل برد
شکل \(\text{1.2}\): یک تابع از مجموعۀ \(D\) به مجموعۀ \(Y\)، یک عنصر یکتا از مجموعۀ \(Y\) را به هر عنصر از مجموعۀ \(D\) مرتبط می سازد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: