خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نمودارهای توابع

اگر \(f\) یک تابع باشد و دامنۀ آن \(D\) باشد، نمودار آن عبارت از نقاطی در صفحۀ مختصات است که مختصات آنها جفت هایی از ورودی-خروجی های \(f\) می باشند. در نشانه گذاری مجموعه ها، نمودار اینگونه خواهد بود:

$$
\{ (x,f(x)) | x \in D \}
$$
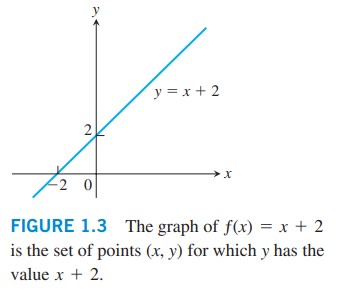
نمودار تابع \(f(x) = x + 2\) عبارت از مجموعه نقاطی با مختصات \((x,y)\) می باشد که در آنها \(y = x+2\) باشد. نمودار این تابع یک خط راست است که در شکل \(\text{1.3}\) می توانید آن را ببینید.
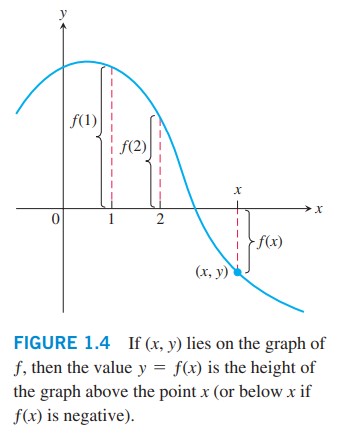
نمودار یک تابع، یک تصویر سودمند از رفتار آن تابع می باشد. اگر \((x,y)\) نقطه ای بر روی نمودار باشد، آن گاه \(y = f(x)\) ارتفاع نمودار در بالا یا پایین نقطۀ \(x\) خواهد بود. این ارتفاع بسته به علامت \(f(x)\) می تواند مثبت یا منفی باشد. (شکل \(\text{1.4}\))

$$
\{ (x,f(x)) | x \in D \}
$$
نمودار تابع \(f(x) = x + 2\) عبارت از مجموعه نقاطی با مختصات \((x,y)\) می باشد که در آنها \(y = x+2\) باشد. نمودار این تابع یک خط راست است که در شکل \(\text{1.3}\) می توانید آن را ببینید.

ترجمۀ شکل:
شکل \(\text{1.3}\): نمودار \(f(x) = x + 2\) عبارت از مجموعه نقاط \((x,y)\) است که در آنها مقدار \(y\) برابر با \(x+2\) می باشد.
شکل \(\text{1.3}\): نمودار \(f(x) = x + 2\) عبارت از مجموعه نقاط \((x,y)\) است که در آنها مقدار \(y\) برابر با \(x+2\) می باشد.
نمودار یک تابع، یک تصویر سودمند از رفتار آن تابع می باشد. اگر \((x,y)\) نقطه ای بر روی نمودار باشد، آن گاه \(y = f(x)\) ارتفاع نمودار در بالا یا پایین نقطۀ \(x\) خواهد بود. این ارتفاع بسته به علامت \(f(x)\) می تواند مثبت یا منفی باشد. (شکل \(\text{1.4}\))

ترجمۀ شکل:
شکل \(\text{1.4}\): اگر \((x,y)\) بر روی نمودار \(f\) قرار گرفته باشد، آن گاه مقدار \(y=f(x)\) ارتفاع نمودار در بالای نقطۀ \(x\) می باشد (یا در صورتی که \(f(x)\) منفی باشد، ارتفاع در پایین نقطۀ \(x\) می باشد).
شکل \(\text{1.4}\): اگر \((x,y)\) بر روی نمودار \(f\) قرار گرفته باشد، آن گاه مقدار \(y=f(x)\) ارتفاع نمودار در بالای نقطۀ \(x\) می باشد (یا در صورتی که \(f(x)\) منفی باشد، ارتفاع در پایین نقطۀ \(x\) می باشد).
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: