نمودار تابع \(y = x^2\) را در بازۀ \([-2 , 2 ]\) ترسیم کنید.

پاسخ

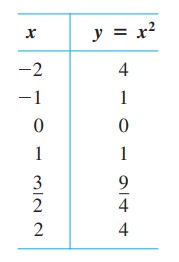
جدولی از جفت مقادیر \(xy\) بسازید که معادلۀ \(y = x^2\) را برآورده سازند.


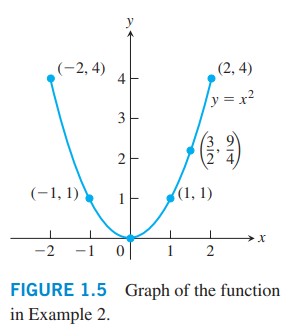
نقاط \((x,y)\) را که مختصاتشان را در جدول می بینید، بر روی نمودار مشخص سازید و یک منحنی نرم که از این نقاط می گذرد، ترسیم کنید. (شکل \(\text{1.5}\) را ببینید).


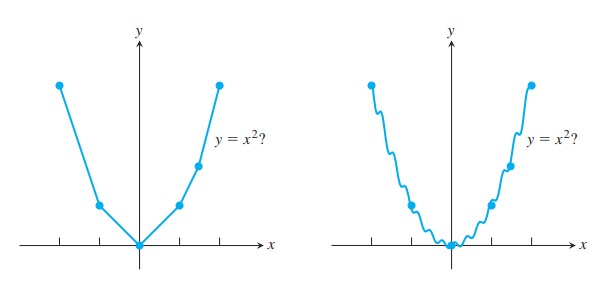
از کجا می دانیم که نمودار \(y = x^2\) شبیه یکی از منحنی های زیر نمی باشد؟


برای فهمیدن این موضوع می توانیم نقاط بیشتری را بر روی نمودار مشخص سازیم. هر چقدر تعداد این نقاط بیشتر باشد، نمودار ما دقیقتر خواهد بود. اما بعد از اینکه نقاط زیادی را ترسیم کردیم، چگونه آنها را به یکدیگر متصل سازیم؟ سوال اساسی همچنان پابرجاست: از کجا می توانیم مطمئن باشیم که نمودار ترسیم شده بین نقاطی که مشخص ساخته ایم چه شکلی خواهد داشت؟ همانطور که در ادامه و در فصل 4 خواهید دید، حسابان به این سوال پاسخ می دهد. فعلاً و تا مشخص شدن قطعی این موضوع، می پذیریم که نقاط را به بهترین وجهی که می توانیم به یکدیگر متصل سازیم.