خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اعداد مثبت (Positive) و منفی (Negative)
اعداد ویژگیهای بسیاری دارند: آنها می توانند بزرگ، کوچک، زوج، فرد، کامل، کسری، مثبت، منفی، و بعضی وقتها سرد و بی تفاوت باشند. (در مورد آخری شوخی کردم!) در فصل 1 اسامی مختلف و دسته بندیهای مختلف اعداد تشریح شدند. در این فصل عمدتاً بر روی دو ویژگی مثبت و منفی بودن اعداد تمرکز می کنیم و اینکه چگونه علامت یک عدد به دستکاری های متفاوت، واکنش نشان می دهد.

این فصل به شما می گوید چگونه جمع، تفریق، ضرب، و تقسیم اعداد علامت دار را، صرفنظر از اینکه همه اعداد دارای علامت یکسان یا اینکه ترکیبی از علامت های مثبت و منفی باشند، انجام بدهید.
در اوایل، ریاضیدانان فهمیدند که استفاده از علامت بعلاوه (plus) و علامت منها (minus) و ایجاد قوانینی برای استفاده از آنها می تواند یک مزیت بزرگ در دنیای اعداد آنها باشد. آنها همچنین متوجه شدند که اگر از علامت منها استفاده کنند، نیازی به ایجاد یک دسته از نمادهای کاملاً جدید برای اعداد منفی (negative numbers) نخواهند داشت. از اینها گذشته، اعداد مثبت و منفی به یکدیگر مرتبط می باشند، و افزودن یک علامت منها در مقابل یک عدد بخوبی کار می کند. اعداد منفی همتایان مثبت دارند و برعکس.
اعدادی که با یکدیگر یکسان هستند اما علامتهایشان فرق می کند، "وارون جمعی" (additive inverses) یکدیگر می باشند. دو عدد وارون جمعی یکدیگر هستند اگر مجموع آنها 0 گردد، بعبارت دیگر:
اعداد مثبت (positive numbers) از 0 بزرگتر هستند. آنها در سمت مقابل 0 نسبت به اعداد منفی قرار دارند. اگر یک مسابقه طناب کشی بین اعداد مثبت و منفی برگزار کنید، اعداد مثبت در سمت راست 0 و اعداد منفی در سمت چپ 0 به خط خواهند شد. (شکل 1-2 را ببیند.)
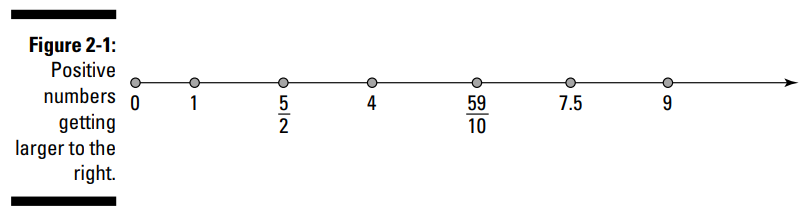
اعداد مثبت هر چقدر از 0 دورتر می شوند، بزرگتر و بزرگتر می گردند: 212 درجه فارنهایت که دمای جوش آب می باشد، از 32 درجه فارنهایت که دمای انجماد آب می باشد، گرمتر می باشد، چرا که 212 نسبت به 32 دورتر از 0 می باشد. هر دو عدد 212 و 32 اعداد مثبت می باشند، اما به نظر می رسد یکی از آنها "مثبت تر" از دیگری است. اگر بخواهید می توانید تفاوت بین آب جوش و یخ را بسنجید تا بدانید چطور یک عدد می تواند از عدد دیگری "مثبت تر" باشد!
درک مفهوم یک عدد کوچکتر از 0 می تواند دشوار باشد. مطمئناً شما می توانید بگویید "کوچکتر از 0"، حتی می توانید کتابی با همین عنوان بنویسید، اما واقعاً معنای آن چیست؟ فکر کنید وارد طبقه همکف یک ساختمان بزرگ دولتی شده اید. شما وارد آسانسور می شوید و باید انتخاب کنید که می خواهید به سمت بالا و طبقه اول، دوم، سوم، یا چهارم بروید، یا اینکه به سمت پایین و طبقه اول، دوم، سوم، چهارم، یا پنجم زیر زمین بروید (همان طبقاتی که تمامی چیزهای مخفی در آنجا نگهداری می شوند). هر چقدر به سمت طبقات پایین بروید و از همکف فاصله بگیرید، فاصله شماره آن طبقه از 0 بیشتر می شود. دومین طبقه زیر زمین می تواند طبقه 2- نامیده شود، اما شاید این یک شماره مناسب برای یک طبقه نباشد.
اعداد منفی از 0 کوچکتر هستند. در یک خط که 0 در مرکز آن قرار دارد، اعداد منفی در سمت چپ 0 به خط می شوند. (شکل 2-2 را ببینید.)
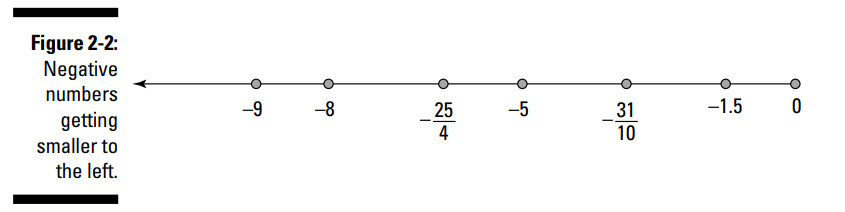
اعداد منفی هرچقدر از 0 دورتر شوند، کوچکتر و کوچکتر می شوند. این وضعیت ممکن است گیج کننده به نظر برسد، چرا که شما ممکن است فکر کنید 400- بزرگتر از 12- می باشد. اما فقط به دمای 400- درجه فارنهایت و 12- درجه فارنهایت فکر کنید. هیچکدام از آنها چیز خوشایندی نیستند که بخواهید به آن فکر کنید، اما 400- درجه فارنهایت قطعاً از 12- درجه فارنهایت کمتر خوشایندتر است. همینطور سردتر، پایینتر، و کوچکتر است.
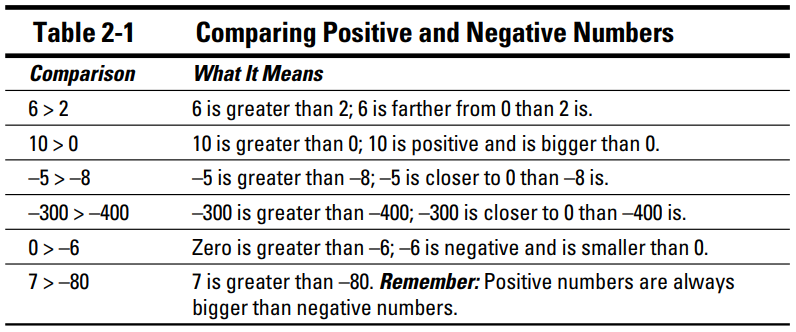
اگرچه مادرم همیشه می گوید "هیچ وقت خودت را با دیگران مقایسه نکن"، با این حال، مقایسه اعداد با اعداد دیگر معمولاً مفید است. هنگامی که که اعداد را با هم مقایسه می کنید، علامت بزرگتر از (<) و علامت کوچکتر از (>) مفید به نظر می رسند. به همین دلیل هم هست که من از آنها در جدول 1-2 که چندین عدد مثبت و منفی را با یکدیگر مقایسه کرده ام، استفاده نموده ام.
بنابراین، اگر بخواهیم اعداد زیر را به ترتیب از کوچک به بزرگ بچینیم:
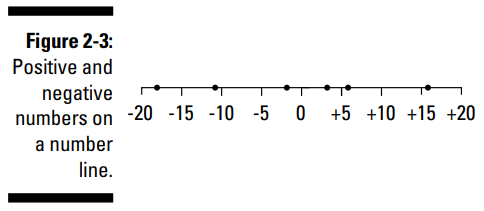
در مورد 0 چطور؟ من اعداد را با استفاده از دوری یا نزدیکی آنها به 0 با یکدیگر مقایسه کردم. آیا 0 عددی مثبت است یا عددی منفی؟ پاسخ اینست که هیچکدام. صفر یک چیز منحصر به فرد است که نه مثبت می باشد و نه منفی. کار صفر جدا کردن اعداد مثبت از اعداد منفی می باشد. چه کار جالبی؟

این فصل به شما می گوید چگونه جمع، تفریق، ضرب، و تقسیم اعداد علامت دار را، صرفنظر از اینکه همه اعداد دارای علامت یکسان یا اینکه ترکیبی از علامت های مثبت و منفی باشند، انجام بدهید.
علامت ها (Signs)
در اوایل، ریاضیدانان فهمیدند که استفاده از علامت بعلاوه (plus) و علامت منها (minus) و ایجاد قوانینی برای استفاده از آنها می تواند یک مزیت بزرگ در دنیای اعداد آنها باشد. آنها همچنین متوجه شدند که اگر از علامت منها استفاده کنند، نیازی به ایجاد یک دسته از نمادهای کاملاً جدید برای اعداد منفی (negative numbers) نخواهند داشت. از اینها گذشته، اعداد مثبت و منفی به یکدیگر مرتبط می باشند، و افزودن یک علامت منها در مقابل یک عدد بخوبی کار می کند. اعداد منفی همتایان مثبت دارند و برعکس.
اعدادی که با یکدیگر یکسان هستند اما علامتهایشان فرق می کند، "وارون جمعی" (additive inverses) یکدیگر می باشند. دو عدد وارون جمعی یکدیگر هستند اگر مجموع آنها 0 گردد، بعبارت دیگر:
a + (–a) = 0اعدادی که با هم وارون جمعی باشند، از نقطه 0 در خط اعداد فاصله یکسانی دارند (البته در جهات متفاوت). برای مثال، وارون جمعی 6- برابر با 6+ می باشد. وارون جمعی 1/5+ برابر با 1/5- می باشد.
اعداد مثبت (positive numbers)
اعداد مثبت (positive numbers) از 0 بزرگتر هستند. آنها در سمت مقابل 0 نسبت به اعداد منفی قرار دارند. اگر یک مسابقه طناب کشی بین اعداد مثبت و منفی برگزار کنید، اعداد مثبت در سمت راست 0 و اعداد منفی در سمت چپ 0 به خط خواهند شد. (شکل 1-2 را ببیند.)
اعداد مثبت هر چقدر از 0 دورتر می شوند، بزرگتر و بزرگتر می گردند: 212 درجه فارنهایت که دمای جوش آب می باشد، از 32 درجه فارنهایت که دمای انجماد آب می باشد، گرمتر می باشد، چرا که 212 نسبت به 32 دورتر از 0 می باشد. هر دو عدد 212 و 32 اعداد مثبت می باشند، اما به نظر می رسد یکی از آنها "مثبت تر" از دیگری است. اگر بخواهید می توانید تفاوت بین آب جوش و یخ را بسنجید تا بدانید چطور یک عدد می تواند از عدد دیگری "مثبت تر" باشد!
اعداد منفی (negative numbers)
درک مفهوم یک عدد کوچکتر از 0 می تواند دشوار باشد. مطمئناً شما می توانید بگویید "کوچکتر از 0"، حتی می توانید کتابی با همین عنوان بنویسید، اما واقعاً معنای آن چیست؟ فکر کنید وارد طبقه همکف یک ساختمان بزرگ دولتی شده اید. شما وارد آسانسور می شوید و باید انتخاب کنید که می خواهید به سمت بالا و طبقه اول، دوم، سوم، یا چهارم بروید، یا اینکه به سمت پایین و طبقه اول، دوم، سوم، چهارم، یا پنجم زیر زمین بروید (همان طبقاتی که تمامی چیزهای مخفی در آنجا نگهداری می شوند). هر چقدر به سمت طبقات پایین بروید و از همکف فاصله بگیرید، فاصله شماره آن طبقه از 0 بیشتر می شود. دومین طبقه زیر زمین می تواند طبقه 2- نامیده شود، اما شاید این یک شماره مناسب برای یک طبقه نباشد.
اعداد منفی از 0 کوچکتر هستند. در یک خط که 0 در مرکز آن قرار دارد، اعداد منفی در سمت چپ 0 به خط می شوند. (شکل 2-2 را ببینید.)
اعداد منفی هرچقدر از 0 دورتر شوند، کوچکتر و کوچکتر می شوند. این وضعیت ممکن است گیج کننده به نظر برسد، چرا که شما ممکن است فکر کنید 400- بزرگتر از 12- می باشد. اما فقط به دمای 400- درجه فارنهایت و 12- درجه فارنهایت فکر کنید. هیچکدام از آنها چیز خوشایندی نیستند که بخواهید به آن فکر کنید، اما 400- درجه فارنهایت قطعاً از 12- درجه فارنهایت کمتر خوشایندتر است. همینطور سردتر، پایینتر، و کوچکتر است.
یادتان باشد: هنگام مقایسه اعداد منفی، عددی که به 0 نزدیکتر باشد، عدد بزرگتر یا بیشتر است.
مقایسه مثبت و منفی
اگرچه مادرم همیشه می گوید "هیچ وقت خودت را با دیگران مقایسه نکن"، با این حال، مقایسه اعداد با اعداد دیگر معمولاً مفید است. هنگامی که که اعداد را با هم مقایسه می کنید، علامت بزرگتر از (<) و علامت کوچکتر از (>) مفید به نظر می رسند. به همین دلیل هم هست که من از آنها در جدول 1-2 که چندین عدد مثبت و منفی را با یکدیگر مقایسه کرده ام، استفاده نموده ام.
نکات فنی: دو علامت دیگر که با علامتهای کوچکتر از و بزرگتر از، در ارتباط می باشند، علامتهای بزرگتر از یا مساوی (≤) و کوچکتر از یا مساوی (≥) می باشند.
بنابراین، اگر بخواهیم اعداد زیر را به ترتیب از کوچک به بزرگ بچینیم:
6, –2, –18, 3, 16, –11خواهیم داشت:
–18, –11, –2, 3, 6, 16این اعداد را به شکل نقاط در خط اعداد شکل 3-2 می بینید.
صفر (Zero)
در مورد 0 چطور؟ من اعداد را با استفاده از دوری یا نزدیکی آنها به 0 با یکدیگر مقایسه کردم. آیا 0 عددی مثبت است یا عددی منفی؟ پاسخ اینست که هیچکدام. صفر یک چیز منحصر به فرد است که نه مثبت می باشد و نه منفی. کار صفر جدا کردن اعداد مثبت از اعداد منفی می باشد. چه کار جالبی؟
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: