خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترتیب انجام عملیات ها (order of operations)

جبر با عبارتهایی آغاز شد که همگی کلمات بودند. هر چیزی عیناً نوشته می شد. با اضافه شدن نمادها و حروف الفبا، به کار بردن جبر ساده تر شد. اما، با اضافه شدن نمادها و نشانه گذاری های بیشتر، قوانین همراه نمادها بخشی از جبر شدند. تمامی این خلاصه نویسی ها فوق العاده هستند، مشروط بر اینکه قوانین آنها را بدانید و مراحلی را که بین آنها وجود دارد، دنبال کنید. ترتیب عملیات ها (order of operations) یک چیز خیلی مهم است که هنگام کار با جبر بارها از آن استفاده می کنید. آن به شما می گوید، در یک مسأله چه کاری را ابتدا، چه کاری را بعد از آن، و کدام کار را در آخر انجام دهید، خواه اینکه جمله ها در نمادهای گروه بندی باشند یا اینکه به توان رسیده باشند.

و از آنجا که شما ممکن است همیشه ترتیب عملیات ها را بدرستی به خاطر نیاورید، بررسی کارتان بسیار مهم می باشد. اطمینان حاصل کردن از اینکه پاسخی که به آن رسیده اید با معنا می باشد، و واقعاً مسأله را حل می کند، مرحله یکی مانده به آخر در هنگام کار با هر مسأله ای می باشد. و سپس مرحله نهایی اینست که مسأله را به شیوه ای بنویسید که سایرین نیز بتوانند به آسانی آن را درک کنند.
این فصل شما را گام به گام با ترتیب عملیات ها، درست آزمایی پاسخهایتان، و نوشتن صحیح آنها، آشنا می سازد.
چه زمانی مهم است که شما کارها را در چه ترتیبی انجام می دهید؟ یا آیا اصلاً اهمیتی دارد؟ خوب، نگاهی به چند موقعیت در دنیای واقعی بیندازیم:
گاهی اوقات ترتیب انجام کارها مهم می باشد، گاهی هم مهم نیستند. در جبر، ترتیب بستگی به این دارد که کدام عملیات ریاضی در حال انجام می باشد. اگر شما صرفاً مشغول جمع زدن هستید یا فقط مشغول ضرب کردن هستید، می توانید از هر ترتیبی که بخواهید استفاده کنید. اما به محض اینکه در یک عبارت چیزهای دیگری را با جمع و ضرب ترکیب کردید، باید به ترتیب صحیح با دقت توجه کنید. شما نمی توانید هر طور که دلتان بخواهد ترتیب انجام عملیات ها را تعیین کنید.
برای مثال، اگر هیچ قانونی برای ترتیب عملیات نباشد، مسأله زیر را به چندین روش مختلف می توان حل کرد. توجه کنید که هر چهار عمل اصلی در این مسأله وجود دارند.
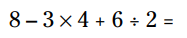
یک روش برای حل این مسأله اینست که صرفاً از سمت چپ به راست عملیات ها را انجام بدهیم:
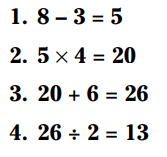
با این روش پاسخ نهایی 13 می شود.
یک رویکرد دیگر اینست که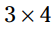 را با پرانتز گروه بندی کنیم. گروه بندی جمله ها به این معنا می باشد که شما الزاماً باید عملیات داخل گروه ها را ابتدا انجام بدهید.
را با پرانتز گروه بندی کنیم. گروه بندی جمله ها به این معنا می باشد که شما الزاماً باید عملیات داخل گروه ها را ابتدا انجام بدهید.
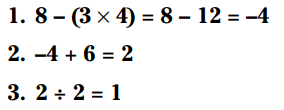
این بار پاسخ نهایی 1 شد.
با استفاده از گروه بندی های دیگری می توانم کاری کنم که پاسخ مسأله 25، 60، و حتی 0 شود. من وارد جزئیات اینکه این پاسخها چطور بدست می آیند نمی شوم، چرا که همه آن پاسخها اشتباه هستند.
ریاضیدانان قواعدی را طراحی کرده اند که همه یک عبارت ریاضی را به یک شیوه یکسان حل کنند و همه به پاسخ یکسان و البته صحیح برسند. در مواقعی که چندین نماد و علامت در عبارت وجود داشته باشد، حل مسأله باید از ابتدا تا انتها به ترتیب خاصی انجام شود. به آن "ترتیب انجام عملیات ها" (order of operations) می گویند.
مثال: عبارت زیر را با استفاده از قوانین ترتیب عملیاتها ساده کنید:

ابتدا تقسیم و ضرب را انجام بدهید،

8 و 11 را با یکدیگر جمع کنید و سپس 18 را تفریق کنید،
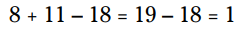
مثال: عبارت زیر را با استفاده از ترتیب عملیات ها ساده کنید:
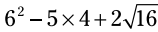
ابتدا توان و ریشه را انجام بدهید:
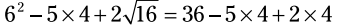
بعد از اینکه رادیکال حذف شد یک نماد ضرب مشخص می شود، تا نشان دهد 2 در نتیجه رادیکال ضرب می گردد. دو عملیات ضرب انجام می شوند تا به برسید. حالا تفریق و جمع را انجام بدهید:
برسید. حالا تفریق و جمع را انجام بدهید: 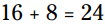 .
.

و از آنجا که شما ممکن است همیشه ترتیب عملیات ها را بدرستی به خاطر نیاورید، بررسی کارتان بسیار مهم می باشد. اطمینان حاصل کردن از اینکه پاسخی که به آن رسیده اید با معنا می باشد، و واقعاً مسأله را حل می کند، مرحله یکی مانده به آخر در هنگام کار با هر مسأله ای می باشد. و سپس مرحله نهایی اینست که مسأله را به شیوه ای بنویسید که سایرین نیز بتوانند به آسانی آن را درک کنند.
این فصل شما را گام به گام با ترتیب عملیات ها، درست آزمایی پاسخهایتان، و نوشتن صحیح آنها، آشنا می سازد.
ترتیب عملیات ها
چه زمانی مهم است که شما کارها را در چه ترتیبی انجام می دهید؟ یا آیا اصلاً اهمیتی دارد؟ خوب، نگاهی به چند موقعیت در دنیای واقعی بیندازیم:
-
هنگامی که خانه را تمیز می کنید، مهم نیست که ابتدا آشپرخانه را تمیز کنید یا اتاق نشیمن را.
-
هنگامی که لباس می پوشید، مهم است که ابتدا کفشتان را بپوشید یا جورابتان را.
گاهی اوقات ترتیب انجام کارها مهم می باشد، گاهی هم مهم نیستند. در جبر، ترتیب بستگی به این دارد که کدام عملیات ریاضی در حال انجام می باشد. اگر شما صرفاً مشغول جمع زدن هستید یا فقط مشغول ضرب کردن هستید، می توانید از هر ترتیبی که بخواهید استفاده کنید. اما به محض اینکه در یک عبارت چیزهای دیگری را با جمع و ضرب ترکیب کردید، باید به ترتیب صحیح با دقت توجه کنید. شما نمی توانید هر طور که دلتان بخواهد ترتیب انجام عملیات ها را تعیین کنید.
برای مثال، اگر هیچ قانونی برای ترتیب عملیات نباشد، مسأله زیر را به چندین روش مختلف می توان حل کرد. توجه کنید که هر چهار عمل اصلی در این مسأله وجود دارند.
یک روش برای حل این مسأله اینست که صرفاً از سمت چپ به راست عملیات ها را انجام بدهیم:
با این روش پاسخ نهایی 13 می شود.
یک رویکرد دیگر اینست که
این بار پاسخ نهایی 1 شد.
با استفاده از گروه بندی های دیگری می توانم کاری کنم که پاسخ مسأله 25، 60، و حتی 0 شود. من وارد جزئیات اینکه این پاسخها چطور بدست می آیند نمی شوم، چرا که همه آن پاسخها اشتباه هستند.
ریاضیدانان قواعدی را طراحی کرده اند که همه یک عبارت ریاضی را به یک شیوه یکسان حل کنند و همه به پاسخ یکسان و البته صحیح برسند. در مواقعی که چندین نماد و علامت در عبارت وجود داشته باشد، حل مسأله باید از ابتدا تا انتها به ترتیب خاصی انجام شود. به آن "ترتیب انجام عملیات ها" (order of operations) می گویند.
قوانین جبر: بر اساس قوانین "ترتیب انجام عملیات ها"، عملیات ها و نمادها را به ترتیب زیر انجام دهید:
-
توان ها و ریشه ها (Powers and roots)
-
ضرب و تقسیم (Multiplication and division)
-
جمع و تفریق (Addition and subtraction)
مثال: عبارت زیر را با استفاده از قوانین ترتیب عملیاتها ساده کنید:
ابتدا تقسیم و ضرب را انجام بدهید،
8 و 11 را با یکدیگر جمع کنید و سپس 18 را تفریق کنید،
مثال: عبارت زیر را با استفاده از ترتیب عملیات ها ساده کنید:
ابتدا توان و ریشه را انجام بدهید:
بعد از اینکه رادیکال حذف شد یک نماد ضرب مشخص می شود، تا نشان دهد 2 در نتیجه رادیکال ضرب می گردد. دو عملیات ضرب انجام می شوند تا به
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: