خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ضرب و تقسیم متغیرها
ضرب کردن متغیرها به نحوی ساده تر از جمع و تفریق آنهاست، درست مثل کسرها - ضرب و تقسیم کسرها ساده تر از جمع و تفریق آنها می باشد زیرا شما مجبور نیستید که مخرج مشترک آنها را پیدا کنید. تنها احتیاط واقعی در زمان تقسیم متغیرها می آید، شما نیاز دارید تا چند قانون نسبتاً سختگیرانه را دنبال کنید تا از تقسیم بر 0 اجتناب نمایید. در این بخش، من نکات و قوانین را به شما می گویم.

هنگامی که متغیرها در یک مسأله ضرب یکسان باشند، ضرب کردن آنها در یکدیگر آنها را به یک فاکتور یا متغیر تنها، فشرده می سازد. شما قادر خواهید بود آن عبارت را با استفاده از توان ها در یک فُرمت کوتاهتر بنویسید. اما، درست مثل جمع و تفریق، شما هنوز هم نمیتوانید متغیرهای متفاوت را با یکدیگر ترکیب کنید.
در اینجا چند مثال از ضرب متغیرها داریم:
هنگامی که می خواهید یک جمله شامل متغیرها و اعداد را بر جمله دیگری تقسیم کنید، اعداد را به شکلی تقسیم کنید که گویی کسرها را ساده می کنید (در مورد ساده کردن کسرها فصل 3 را ببینید). اما فقط متغیرهای یکسان می توانند بر یکدیگر تقسیم شوند.
در تقسیم اعداد کامل (whole numbers) مثل 5 ÷ 27 الزامی نیست نتیجه تقسیم برابر شود. تقسیم می تواند دارای باقیمانده باشد (مقداری که بعد از تقسیم عددی بر عدد دیگر بر جای می ماند). اما هنگامی که عبارتهای جبری را تقسیم می کنید، معمولاً باقیمانده ها را نمی خواهید - باقیمانده ها جملات جدیدی خواهند بود. بنابراین، مطمئن شوید آنجا هیچ باقیمانده ای برجای نمی گذارید.
ابتدا، به من اجازه دهید تا این قانون را با قوطی های آلومینیومی نشان بدهم.
مثال: چهار دوست تصمیم گرفتند قوطی های آلومینیومی را برای بازیافت (و پول) جمع آوری کنند. آنها 12x3 قوطی جمع آوری کردند، و قرار است که بابت هر قوطی y2 سنت (cents) دریافت کنند. با این حساب مجموع پولی که جمع آوری می شود 12x3y2 می باشد. آنها چگونه این پول را تقسیم می کنند؟
مجموع مبلغ را بر 4 تقسیم کنید تا مبلغی را که هر کدام از این چهار نفر دریافت می کند، بدست آورید:
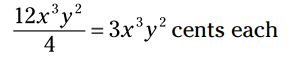
تنها چیزی که در اینجا تقسیم شد ضریب بود. اگر بخواهید تعداد قوطی های هر شخص را بدست آورید، به جای تقسیم بر 4 بر 4y2 تقسیم را انجام بدهید:
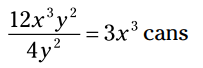
چرا در این معمای داستانی قوطی های آلومینیومی استفاده از متغیرها بهتر از استفاده از اعداد می باشد؟ زیرا اگر تعداد قوطی ها یا ارزش مالی هر قوطی تغییر کند، هنوز هم همه سهم های افراد به درستی کار خواهد کرد. فقط کافیست مقادیر تغییر یافته را در x و y قرار بدهید.
مثالهای زیر به شما نشان می دهند چگونه با استفاده از متغیرها، ضرایب، و توانها، تقسیم را انجام بدهید.
با استفاده از تقسیم عبارتهای جبری، مسأله های زیر را حل کنید:
من در این فصل چهار عملیات اصلی - جمع، تفریق، ضرب، و تقسیم - را پوشش دادم. اما بسیاری از مسأله های جبر با بیش از یک عملیات درگیر هستند، بنابراین مراحل بعدی را ببینید تا چگونگی رسیدگی به ترکیبی از عملیات ها را بدانید.
در این مسأله بعدی، شما ضرب و تقسیم را می بینید. همچنین ترتیب عملیات ها نیز اعمال می گردد، همچنین قوانین ترکیب فاکتورها و جمله ها نیز وجود دارند و مورد استفاده قرار گرفته اند.
مثال: این عبارت را ساده کنید:
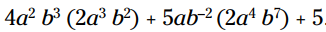
بسیار خوب. اکنون که با موفقیت به مقابله چالش انجام چندین عملیات در یک مثال پیچیده رفتید، چرا تلاش نکنید دوباره وارد این مراحل شوید و ترکیبی از عملیات ها را روی مثالی دیگر اجرا کنید؟
مثال: این عبارت را ساده کنید:

مثال بعدی شانس شما برای به رُخ کشیدن تواناییهایتان به سایرین می باشد. شما ضرب را انجام داده اید، بنابراین مرحله بعد تقسیم می باشد (که در واقع یک تفریق ساده می باشد). بزن بریم!
مثال: این عبارت را ساده کنید:


ضرب متغیرها
هنگامی که متغیرها در یک مسأله ضرب یکسان باشند، ضرب کردن آنها در یکدیگر آنها را به یک فاکتور یا متغیر تنها، فشرده می سازد. شما قادر خواهید بود آن عبارت را با استفاده از توان ها در یک فُرمت کوتاهتر بنویسید. اما، درست مثل جمع و تفریق، شما هنوز هم نمیتوانید متغیرهای متفاوت را با یکدیگر ترکیب کنید.
قوانین جبر: هنگامی که فاکتورهای دارای متغیرها را در یکدیگر ضرب می کنید، ضرایب و متغیرها را مانند معمول در یکدیگر ضرب نمایید. اگر پایه های آنها یکسان باشند، شما می توانید صرفاً با جمع زدن توانهای آنها، در یکدیگر ضربشان کنید. (اطلاعات بیشتر در مورد ضرب توانها را در فصل 4 ببینید.)
در اینجا چند مثال از ضرب متغیرها داریم:
-
: دو فاکتور a با یک توان ترکیب می شوند تا تعداد دفعات ضرب را درعبارت نشان بدهد.
-
-
: حاصلضرب سه عدد در یکدیگر 24 می شود. ضرب یک عملیات جابجایی پذیر (commutative) می باشد، بنابراین شما می توانید آنها را در هر ترتیبی در یکدیگر ضرب کنید.
-
: در فاکتورهای مشترک، توانها را با یکدیگر جمع بزنید.
-
-
تقسیم متغیرها
هنگامی که می خواهید یک جمله شامل متغیرها و اعداد را بر جمله دیگری تقسیم کنید، اعداد را به شکلی تقسیم کنید که گویی کسرها را ساده می کنید (در مورد ساده کردن کسرها فصل 3 را ببینید). اما فقط متغیرهای یکسان می توانند بر یکدیگر تقسیم شوند.
در تقسیم اعداد کامل (whole numbers) مثل 5 ÷ 27 الزامی نیست نتیجه تقسیم برابر شود. تقسیم می تواند دارای باقیمانده باشد (مقداری که بعد از تقسیم عددی بر عدد دیگر بر جای می ماند). اما هنگامی که عبارتهای جبری را تقسیم می کنید، معمولاً باقیمانده ها را نمی خواهید - باقیمانده ها جملات جدیدی خواهند بود. بنابراین، مطمئن شوید آنجا هیچ باقیمانده ای برجای نمی گذارید.
قوانین جبر: هنگام تقسیم متغیرها، مسأله را به شکل یک کسر بنویسید. با استفاده از بزرگترین فاکتور مشترک (GCF:Greatest Common Factor)، اعداد را تقسیم کرده و کاهش بدهید. برای تقسیم متغیرهای مشابه یکدیگر از قوانین تقسیم توانها که در فصل 4 گفتیم، استفاده کنید. تقسیم کردن متغیرها نسبتاً ساده و سرراست است. هر متغیر به صورت جداگانه در نظر گرفته می شود. اعداد ضرایب نیز مشابه کسرهای ساده کاهش پیدا می کنند.
ابتدا، به من اجازه دهید تا این قانون را با قوطی های آلومینیومی نشان بدهم.
مثال: چهار دوست تصمیم گرفتند قوطی های آلومینیومی را برای بازیافت (و پول) جمع آوری کنند. آنها 12x3 قوطی جمع آوری کردند، و قرار است که بابت هر قوطی y2 سنت (cents) دریافت کنند. با این حساب مجموع پولی که جمع آوری می شود 12x3y2 می باشد. آنها چگونه این پول را تقسیم می کنند؟
مجموع مبلغ را بر 4 تقسیم کنید تا مبلغی را که هر کدام از این چهار نفر دریافت می کند، بدست آورید:
تنها چیزی که در اینجا تقسیم شد ضریب بود. اگر بخواهید تعداد قوطی های هر شخص را بدست آورید، به جای تقسیم بر 4 بر 4y2 تقسیم را انجام بدهید:
چرا در این معمای داستانی قوطی های آلومینیومی استفاده از متغیرها بهتر از استفاده از اعداد می باشد؟ زیرا اگر تعداد قوطی ها یا ارزش مالی هر قوطی تغییر کند، هنوز هم همه سهم های افراد به درستی کار خواهد کرد. فقط کافیست مقادیر تغییر یافته را در x و y قرار بدهید.
مثالهای زیر به شما نشان می دهند چگونه با استفاده از متغیرها، ضرایب، و توانها، تقسیم را انجام بدهید.
با استفاده از تقسیم عبارتهای جبری، مسأله های زیر را حل کنید:
-
اگر a نشان دهنده تعداد سیب ها (apples) باشد، ده سیب تقسیم بر گروه هایی متشکل از پنج سیب، می شود دو گروه (دقت کنید دو گروه و نه دو سیب):
-
ده سیب تقسیم بر پنج گروه می شود دو سیب در هر گروه:
-
ساده سازی عبارت:
. شش تقسیم بر سه می شود دو. با استفاده از قانون تقسیم توان ها داریم:
.
-
ساده سازی عبارت:
.من ترجیح می دهم تا پاسخ را با یک x و توان مثبت در مخرج کسر بنویسم، تا اینکه آن را با توان منفی در صورت کسر بیاورم.
-
و یک ساده سازی دیگر:
همه را با هم انجام بدهید
من در این فصل چهار عملیات اصلی - جمع، تفریق، ضرب، و تقسیم - را پوشش دادم. اما بسیاری از مسأله های جبر با بیش از یک عملیات درگیر هستند، بنابراین مراحل بعدی را ببینید تا چگونگی رسیدگی به ترکیبی از عملیات ها را بدانید.
در این مسأله بعدی، شما ضرب و تقسیم را می بینید. همچنین ترتیب عملیات ها نیز اعمال می گردد، همچنین قوانین ترکیب فاکتورها و جمله ها نیز وجود دارند و مورد استفاده قرار گرفته اند.
مثال: این عبارت را ساده کنید:
-
در هر جمله فاکتورها را باز چینش کنید تا بتوانید متغیرها را جداگانه در یکدیگر ضرب کنید.
-
اعداد را در یکدیگر ضرب کنید و توانهای متغیرهای شبیه هم را نیز با یکدیگر جمع بزنید.
شما می توانید ببینید که دو جمله اول شبیه یکدیگرند زیرا هم متغیرهایشان و هم توان متغیرهایشان یکسان می باشد، به همین دلیل می توانید آنها را با یکدیگر جمع بزنید.
-
جملات مشابه را با یکدیگر ترکیب کنید.
بسیار خوب. اکنون که با موفقیت به مقابله چالش انجام چندین عملیات در یک مثال پیچیده رفتید، چرا تلاش نکنید دوباره وارد این مراحل شوید و ترکیبی از عملیات ها را روی مثالی دیگر اجرا کنید؟
مثال: این عبارت را ساده کنید:
-
در هر جمله فاکتورها را بازچینش کنید تا بتوانید متغیرها را جداگانه در یکدیگر ضرب کنید.
-
اعداد را در یکدیگر ضرب کنید و توانهای متغیرهای شبیه یکدیگر را با هم جمع بزنید.
-
جملات یکسان را ترکیب کنید.
در این مورد، تنها دو جمله اول می توانند با هم ترکیب شوند، متغیرهای آنها و توانهای آنها با هم مطابقت دارند.
مثال بعدی شانس شما برای به رُخ کشیدن تواناییهایتان به سایرین می باشد. شما ضرب را انجام داده اید، بنابراین مرحله بعد تقسیم می باشد (که در واقع یک تفریق ساده می باشد). بزن بریم!
مثال: این عبارت را ساده کنید:
-
با تفریق کردن توانهای پایه های مشترک تقسیم را انجام بدهید.
اعداد شناخته شده را تقسیم کنید. فرض کنید که پایه های بدون توان، دارای توان 1 می باشند. این مسأله دارای توانهای منفی هم در صورت و هم در مخرج کسرها می باشد که باید با آنها سر و کار داشته باشید.
-
تفریق توانها را تکمیل کنید.
نکته: هنگامی که توان منفی در x-5 که در مخرج کسر قرار دارد بالا آورده شود، تبدیل به توان مثبت می شود و جمع می گردد. توان های کسری درست مثل توانهای اعداد کامل کار می کنند، آنها را هم به شیوه یکسانی جمع یا تفریق کنید.
-
جملاتی را که دقیقاً مشابه هستند - اعدادی که دارای متغیرها و توانهای مشترک می باشند - جمع یا تفریق کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: