خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
در نظر گرفتن فاکتورهای اول
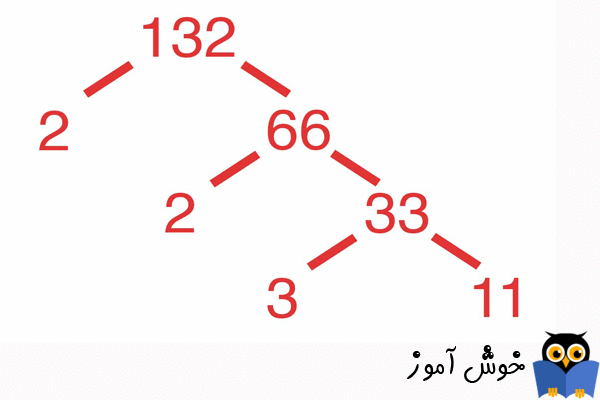
اگر بتوانید تشخیص دهید کدام اعداد مرکب (composite) و کدام اعداد اول (prime) هستند، فاکتورگیری در جبر ساده تر می شود. اگر بدانید یک عدد به کدام دسته بندی تعلق دارد، خواهید دانست با آن چه کار کنید. هنگام کاهش کسرها یا فاکتورگیری از عبارات چند جمله ای، شما به دنبال چیزهای مشترک بین اعداد می گردید. اگر عددی اول باشد، شما جستجو را متوقف خواهید کرد. اکنون، سعی کنید تمامی این دانش ها را به کار ببندید!

فاکتورهای اول (Prime factorizations) در هنگام کاهش کسرها، مفیدند. مطمئناً شما می توانید به صورت تکراری مدام کسرها را کاهش بدهید تا به نتیجه مطلوب برسید - ابتدا صورت و مخرج کسر را بر 5 تقسیم کنید، سپس هر دوی آنها را بر 3 تقسیم کنید، و به همین ترتیب ادامه بدهید. اما یک روش بسیار کارآمدتر برای استفاده بهتر از زمانتان اینست که فاکتورهای اول صورت و مخرج کسر را بنویسید و سپس کار پیدا کردن فاکتورهای مشترک بین صورت و مخرج کسر بسیار ساده خواهد شد.
مثال: کسر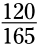 را با دنبال کردن این مراحل، کاهش بدهید:
را با دنبال کردن این مراحل، کاهش بدهید:
مثال: اکنون سعی کنید کسر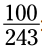 را ساده کنید:
را ساده کنید:
به فاکتورهای اول بنگرید. شما می توانید ببینید که صورت و مخرج کسر مطلقاً هیچ چیز مشترکی ندارند. این کسر نمی تواند کاهش یابد. این دو عدد در ارتباط با یکدیگر اول می باشند (relatively prime). زیبایی استفاده از فاکتورهای اول اینست که شما می توانید مطمئن باشید کاهش کسر خاتمه یافته است و شما چیزی را از قلم نینداخته اید. شما می توانید کسر را در همین شکل فاکتورهای اول آن رها کنید یا به شکل ساده قبلی یعنی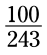 برگردید. بستگی به ترجیح خود شما دارد.
برگردید. بستگی به ترجیح خود شما دارد.
در ادامه، من چند متغیر به این ترکیب اضافه می کنم.
مثال: این کسر را کاهش بدهید: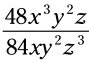
با نوشتن فاکتورهای اول، شما می توانید خاطر جمع شوید که هیچ فاکتوری را که ممکن است بین صورت و مخرج کسر مشترک باشد، فراموش نکرده اید.
مثال: این کسر را کاهش بدهید:
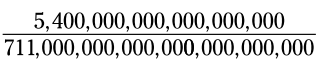
بیرون کشیدن فاکتورهای مشترک از لیستی از جملات یا مجموع یا اختلاف بین یک دسته از جملات به یک دلیل خوب انجام می شود. در هنگام ساده سازی عبارات و حل کردن معادلات این یک کار متداول است. فاکتور مشترکی که بزرگترین تفاوت را در این نوع مسأله ها ایجاد می کند، بزرگترین فاکتور مشترک (GCF:Greatest Common Factor) می باشد. بهترین کار اینست که بزرگترین فاکتور مشترک را شناسایی کنید و آن را فاکتور بگیرید.
در هر مبحث فاکتورگیری، بزرگترین فاکتور مشترک، رایج ترین و ساده ترین روش فاکتورگیری می باشد، و همیشه مهمترین چیز است. و در هنگام حل کردن معادلات مفید است که در مورد بزرگترین فاکتور مشترک بدانید. در یک عبارت که دو یا بیشتر جمله دارد، پیدا کردن بزرگترین فاکتور مشترک می تواند عبارت را قابل درک تر و قابل مدیریت تر کند.
در هنگام ساده سازی عبارات، بهترین سناریوی ممکن اینست که بزرگترین فاکتور مشترک را در یک لیست از جملات شناسایی کرده و بیرون بکشید. اگرچه گاهی اوقات بزرگترین فاکتور مشترک چندان قابل تشخیص نمی باشد. ممکن است چند فاکتور عجیب مثل 7، 13، یا 23 داشته باشد. اگر نتوانید یکی از این اعداد را به عنوان ضریب (multiplier) شناسایی کنید، دنیا به آخر نمی رسد، فقط اگر بشود قشنگ تر است.
سه جمله موجود در عبارت زیر دارای فاکتور مشترکی می باشند. بزرگترین فاکتور مشترک آنها چیست؟
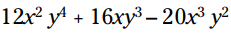 این مراحل به شما کمک می کنند آن را پیدا کنید.
این مراحل به شما کمک می کنند آن را پیدا کنید.
مثال: در اینجا چگونگی پیدا کردن بزرگترین فاکتور مشترک و نوشتن فاکتورگیری عبارت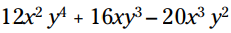 را می بینید:
را می بینید:
در مثالهای بعدی، نسخه کوتاه شده این مراحل را به شما نشان می دهم.
مثال: بزرگترین فاکتور مشترک را پیدا کنید و نتیجه فاکتورگیری را بنویسد:
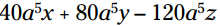
مثال: بزرگترین فاکتور مشترک را پیدا کنید و نتیجه فاکتورگیری را بنویسد:
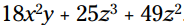
با وجود اینکه هیچ کدام از این جملات اول (prime) نیستند، این سه جمله هیچ چیز مشترکی با یکدیگر ندارند. فاکتورهای اول زیر این مسأله را نشان می دهد:
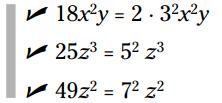
دو جمله آخر فاکتوری از z را مشترکاً دارند، اما جمله اول ندارد. در این گونه مواقع اصطلاحاً گفته می شود این عبارت اول (prime) است، زیرا قابل فاکتورگیری نمی باشد.

به حساب آوردن اعداد اول
فاکتورهای اول (Prime factorizations) در هنگام کاهش کسرها، مفیدند. مطمئناً شما می توانید به صورت تکراری مدام کسرها را کاهش بدهید تا به نتیجه مطلوب برسید - ابتدا صورت و مخرج کسر را بر 5 تقسیم کنید، سپس هر دوی آنها را بر 3 تقسیم کنید، و به همین ترتیب ادامه بدهید. اما یک روش بسیار کارآمدتر برای استفاده بهتر از زمانتان اینست که فاکتورهای اول صورت و مخرج کسر را بنویسید و سپس کار پیدا کردن فاکتورهای مشترک بین صورت و مخرج کسر بسیار ساده خواهد شد.
مثال: کسر
-
فاکتورهای اول صورت کسر را بدست آورید.
-
فاکتورهای اول مخرج کسر را بدست آورید.
-
سپس، کسر را با استفاده از فاکتورهای اول آن بنویسید.
-
فاکتورهای مشترک بین صورت و مخرج کسر را خط بزنید تا ببینید چه چیزی باقی می ماند - شکل کاهش یافته.
مثال: اکنون سعی کنید کسر
-
فاکتورهای اول صورت کسر را بیابید.
-
فاکتورهای اول مخرج کسر را بیابید.
-
کسر را با فاکتورهای اول آن بنویسید.
به فاکتورهای اول بنگرید. شما می توانید ببینید که صورت و مخرج کسر مطلقاً هیچ چیز مشترکی ندارند. این کسر نمی تواند کاهش یابد. این دو عدد در ارتباط با یکدیگر اول می باشند (relatively prime). زیبایی استفاده از فاکتورهای اول اینست که شما می توانید مطمئن باشید کاهش کسر خاتمه یافته است و شما چیزی را از قلم نینداخته اید. شما می توانید کسر را در همین شکل فاکتورهای اول آن رها کنید یا به شکل ساده قبلی یعنی
در ادامه، من چند متغیر به این ترکیب اضافه می کنم.
مثال: این کسر را کاهش بدهید:
-
فاکتورهای اول صورت کسر را بیابید.
-
فاکتورهای اول مخرج کسر را بیابید.
-
کسر را با فاکتورهای اول آن بنویسید.
-
فاکتورهای مشترک را خط بزنید.
با نوشتن فاکتورهای اول، شما می توانید خاطر جمع شوید که هیچ فاکتوری را که ممکن است بین صورت و مخرج کسر مشترک باشد، فراموش نکرده اید.
مثال: این کسر را کاهش بدهید:
-
فاکتورهای اول صورت کسر را بیابید.
با استفاده از این فرصت که این اعداد دارای صفرهای زیادی هستند، آنها را با یک نوع از نماد علمی بازنویسی کنید.
-
فاکتورهای اول مخرج کسر را بیابید، دوباره از نماد علمی استفاده کنید.
-
کسر را با فاکتورهای اول آن بنویسید.
-
فاکتورهای مشترک را خط بزنید.
عدد 2 در صورت کسر و عدد 10 در مخرج کسر یک فاکتور مشترک از 2 دارند.
بیرون کشیدن فاکتورها و رها کردن بقیه
بیرون کشیدن فاکتورهای مشترک از لیستی از جملات یا مجموع یا اختلاف بین یک دسته از جملات به یک دلیل خوب انجام می شود. در هنگام ساده سازی عبارات و حل کردن معادلات این یک کار متداول است. فاکتور مشترکی که بزرگترین تفاوت را در این نوع مسأله ها ایجاد می کند، بزرگترین فاکتور مشترک (GCF:Greatest Common Factor) می باشد. بهترین کار اینست که بزرگترین فاکتور مشترک را شناسایی کنید و آن را فاکتور بگیرید.
قوانین جبر: بزرگترین فاکتور مشترک (greatest common factor) بزرگترین عدد ممکن است که در یک عبارت دارای دو یا چند جمله، هر جمله را به صورت مساوی تقسیم می کند (یا صورت و مخرج یک کسر را به صورت مساوی تقسیم می کند).
در هر مبحث فاکتورگیری، بزرگترین فاکتور مشترک، رایج ترین و ساده ترین روش فاکتورگیری می باشد، و همیشه مهمترین چیز است. و در هنگام حل کردن معادلات مفید است که در مورد بزرگترین فاکتور مشترک بدانید. در یک عبارت که دو یا بیشتر جمله دارد، پیدا کردن بزرگترین فاکتور مشترک می تواند عبارت را قابل درک تر و قابل مدیریت تر کند.
در هنگام ساده سازی عبارات، بهترین سناریوی ممکن اینست که بزرگترین فاکتور مشترک را در یک لیست از جملات شناسایی کرده و بیرون بکشید. اگرچه گاهی اوقات بزرگترین فاکتور مشترک چندان قابل تشخیص نمی باشد. ممکن است چند فاکتور عجیب مثل 7، 13، یا 23 داشته باشد. اگر نتوانید یکی از این اعداد را به عنوان ضریب (multiplier) شناسایی کنید، دنیا به آخر نمی رسد، فقط اگر بشود قشنگ تر است.
سه جمله موجود در عبارت زیر دارای فاکتور مشترکی می باشند. بزرگترین فاکتور مشترک آنها چیست؟
-
فاکتورهای مشترک عددی را تعیین کنید.
-
فاکتورهای مشترک متغیرها را تعیین کنید.
-
فاکتورهای اول هر جمله را بنویسید.
-
بزرگترین فاکتور مشترک را پیدا کنید.
-
هر جمله را بر بزرگترین فاکتور مشترک تقسیم کنید.
-
نتیجه را به شکل حاصلضربی از بزرگترین فاکتور مشترک در نتیجه تقسیم بنویسید.
مثال: در اینجا چگونگی پیدا کردن بزرگترین فاکتور مشترک و نوشتن فاکتورگیری عبارت
-
فاکتورهای مشترک عددی را تعیین کنید.
هر جمله ضریبی دارد که بر توانی از 2 بخش پذیر می باشد، که 4 = 22 است.
-
فاکتورهای مشترک متغیرها را تعیین کنید.
هر جمله دارای فاکتورهای x و y می باشد.
-
فاکتورهای اول هر جمله را بنویسید.
-
بزرگترین فاکتور مشترک را پیدا کنید.
بزرگترین فاکتور مشترک حاصلضرب تمامی فاکتورهای مشترک بین این سه جمله می باشد. بزرگترین فاکتور مشترک شامل کمترین توان از هر متغیر و عدد می باشد که در هر کدام از این جملات رخ داده است. هر عدد در این مثال فاکتوری از 2 دارد. اگر کمترین توان 2 که در تمامی فاکتورها دیده می شود 22 باشد، سپس 22 بخشی از بزرگترین فاکتور مشترک می باشد.
هر فاکتوری توانی از x دارد. اگر کمترین توان x که در هر فاکتور وجود دارد 1 باشد، سپس x1 بخشی از بزرگترین فاکتور مشترک می باشد.
هر فاکتوری توانی از y دارد. اگر کمترین توان y که در هر فاکتور وجود دارد 2 باشد، سپس y2 بخشی از بزرگترین فاکتور مشترک می باشد.
بزرگترین فاکتور مشترک این عبارت به شرح زیر می باشد:
-
هر جمله را بر بزرگترین فاکتور مشترک تقسیم کنید.
جملات مربوطه به ترتیب به شکل زیر تقسیم می شوند:
توجه داشته باشید که سه نتیجه متفاوت تقسیم هیچ چیز مشترکی ندارند. هر کدام از دو نتیجه اول یک y دارد و اولی و سومی هر دو یک x دارند، اما هیچ چیزی بین هر سه نتیجه مشترک نمی باشد. این بهترین وضعیت فاکتورگیری می باشد که ممکن است بخواهید.
-
نتیجه را به شکل حاصلضربی از بزرگترین فاکتور مشترک در نتیجه تقسیم بنویسید.
عبارت اصلی را با بزرگترین فاکتور مشترک در خارج یک جفت پرانتز بازنویسی کنید.
در مثالهای بعدی، نسخه کوتاه شده این مراحل را به شما نشان می دهم.
مثال: بزرگترین فاکتور مشترک را پیدا کنید و نتیجه فاکتورگیری را بنویسد:
40a5x + 80a5y – 120a5z = 40a5(x + 2y – 3z)
مثال: بزرگترین فاکتور مشترک را پیدا کنید و نتیجه فاکتورگیری را بنویسد:
با وجود اینکه هیچ کدام از این جملات اول (prime) نیستند، این سه جمله هیچ چیز مشترکی با یکدیگر ندارند. فاکتورهای اول زیر این مسأله را نشان می دهد:
دو جمله آخر فاکتوری از z را مشترکاً دارند، اما جمله اول ندارد. در این گونه مواقع اصطلاحاً گفته می شود این عبارت اول (prime) است، زیرا قابل فاکتورگیری نمی باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: