خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توزیع جبری (Algebraic distribution)

جبر مملو از کارهای متناقض است. ابتدا از شما می خواهند تا فاکتور بگیرید (برای اطلاعات بیشتر در مورد فاکتورگیری، فصلهای 8، 9، و 10 را ببینید) و سپس می خواهند توزیع کنید. یا مثالی دیگر: ابتدا از شما می خواهند کسر را کاهش بدهید، و سپس قرار می شود تا ضرب کنید و اعداد بزرگتری بسازید. ابتدا از شما می خواهند عبارت ریاضی را فشرده سازید، و سپس می خواهند آن را دوباره گسترش بدهید. تصمیم خودت را بگیر!

اما مطمئن باشید دلایل خوبی پشت انجام همه این فرآیندهای به ظاهر متناقض وجود دارد. شما یک هدیه تولد را با دقت بسته بندی می کنید تا روز بعد بسته بندی اش باز شود. شما به چمن هایتان آب و کود می دهید تا رشد کنند، اما بعد کوتاهشان می کنید. می بینید، تناقض ها همه جا هستند!
در این فصل، به شما می گویم چه وقت، چرا، و چگونه فاکتور بگیرید و توزیع کنید. شما می خواهید تصمیمات آگاهانه بگیرید و سپس مهارتهایی داشته باشید که آنها را بدرستی اجرا کنید. اینکه یک آیپاد (iPod) بخرید ولی ندانید با آن باید چکار کنید، چه ارزشی خواهد داشت؟
هنگامی که چیزها به صورت منصفانه به اشتراک گذاشته شوند، به هرکسی یا هرچیزی که شامل آن باشد سهم برابری می رسد - فقط یکی از سهم ها - نه دوبرابر آنچه که به دیگران رسیده است. وقتیکه یک کودک کیک تولدش را بین همکلاسی هایش تقسیم می کند، به این شکل است که: "یکی برای تو، و یکی برای تو ...". در بازی مانکالا (Mancala) - مانکالا یک بازی فکری می باشد - سنگهای هر محفظه به شکل یکی برای هر کدام بین محفظه های بعدی توزیع می گردد تا سنگها تمام شوند. هر روش دیگری تقلب است! توزیع در جبر نیز فرآیند مشابهی دارد - به هر کدام یک سهم می رسد.
توزیع اقلام (Distributing items) یک عمل است که طی آن اقلام را به صورت برابر گسترش می دهیم. توزیع جبری (Algebraic distribution) به این معنا می باشد که هر کدام از جملات داخل پرانتزها را در جمله دیگری که در بیرون پرانتز قرار دارد، ضرب کنیم. هر جمله در یک مقدار یکسان ضرب می گردد.
مثال: عدد 2 را در عبارت زیر توزیع کنید:
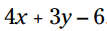
وقتیکه چند فاکتور را در چندین جمله توزیع می کنید، مقدار عبارت اصلی را تغییر نمی دهید. خواه اینکه ابتدا توزیع را انجام بدهید یا اینکه ابتدا چیزهای داخل پرانتزها را با یکدیگر جمع بزنید، پاسخ یکسان است. هنگامی که دستکاری های جبری (algebraic manipulations) را انجام می دهید، اغلب مجبور می شوید که بر اساس تجربیات قبلیتان در جبر، یک تصمیم سرنوشت ساز بگیرید که آیا ابتدا چیزهای داخل پرانتز را با هم ترکیب کنید یا ابتدا توزیع را انجام بدهید.
گاهی اوقات شما صرفاً با نگاه کردن می توانید بگویید که آیا ساده تر اینست که ابتدا جمله بیرون پرانتز را توزیع کنید یا اینکه ابتدا عبارات داخل پرانتز را ترکیب کنید. یک لحظه صبر کردن و فکر کردن به اینکه کدام رویکرد می تواند بهتر باشد ممکن است در بلند مدت در زمان شما صرفه جویی کند.
مثال: با پیدا کردن حاصلضرب این عبارت را ساده کنید:
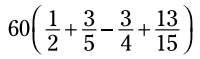
ببینید اگر شما بعد از اینکه کسرها را با یکدیگر جمع زدید، 60 را در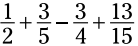 ضرب کنید، چقدر پیچیده می شود. شما باید یک مخرج مشترک بین کسرها پیدا کنید و کسرها را جمع و تفریق کنید:
ضرب کنید، چقدر پیچیده می شود. شما باید یک مخرج مشترک بین کسرها پیدا کنید و کسرها را جمع و تفریق کنید:
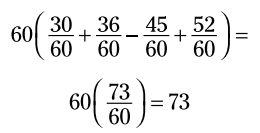
اکنون به انتخاب بهتر بنگرید، جایی که ابتدا توزیع انجام می شود:
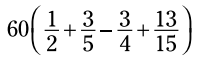
با ضرب کردن در 60 از شر تمامی کسرها خلاص می شوید، بنابراین نیازی به پیدا کردن مخرج مشترک هم ندارید.
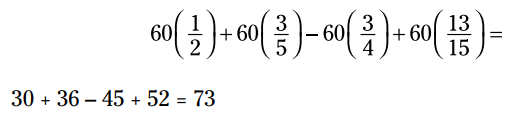
آیا مزایای توزیع در ابتدا را در این مورد دیدید؟ برای یک مثال از وضعیتی که جمع زدن در ابتدا بهتر می باشد، بخش بعدی را ببیند.
قبل از شروع مراحل حل کردن یک مسأله توزیع، به اندازه اعداد نگاه کنید. اگر اعداد بزرگ باشند، سپس توزیع یک جمله بزرگ روی یک جمله بزرگتر دیگر در داخل پرانتزها صرفاً می تواند منجر به این شود که هر جمله بزرگتر شود و کمتر قابل مدیریت باشد. در مورد اعداد بزرگ، ممکن است ساده تر باشد که کار را از انجام جمع و تفریق های ساده در داخل پرانتزها شروع کنید، و سپس جمله بیرون پرانتز را بر روی موارد داخل پرانتز توزیع کنید.
مثال: این عبارت را ساده کنید:
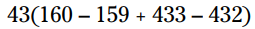
اگر بخواهیم اول 43 را توزیع کنیم (اوه چه کاری!):
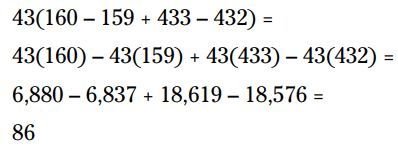
حالا به انتخاب بهتر بنگرید، جاییکه ابتدا عبارتهای داخل پرانتز را ترکیب می کنید:
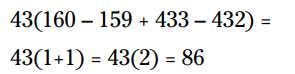

اما مطمئن باشید دلایل خوبی پشت انجام همه این فرآیندهای به ظاهر متناقض وجود دارد. شما یک هدیه تولد را با دقت بسته بندی می کنید تا روز بعد بسته بندی اش باز شود. شما به چمن هایتان آب و کود می دهید تا رشد کنند، اما بعد کوتاهشان می کنید. می بینید، تناقض ها همه جا هستند!
در این فصل، به شما می گویم چه وقت، چرا، و چگونه فاکتور بگیرید و توزیع کنید. شما می خواهید تصمیمات آگاهانه بگیرید و سپس مهارتهایی داشته باشید که آنها را بدرستی اجرا کنید. اینکه یک آیپاد (iPod) بخرید ولی ندانید با آن باید چکار کنید، چه ارزشی خواهد داشت؟
یکی برای هر کدام
هنگامی که چیزها به صورت منصفانه به اشتراک گذاشته شوند، به هرکسی یا هرچیزی که شامل آن باشد سهم برابری می رسد - فقط یکی از سهم ها - نه دوبرابر آنچه که به دیگران رسیده است. وقتیکه یک کودک کیک تولدش را بین همکلاسی هایش تقسیم می کند، به این شکل است که: "یکی برای تو، و یکی برای تو ...". در بازی مانکالا (Mancala) - مانکالا یک بازی فکری می باشد - سنگهای هر محفظه به شکل یکی برای هر کدام بین محفظه های بعدی توزیع می گردد تا سنگها تمام شوند. هر روش دیگری تقلب است! توزیع در جبر نیز فرآیند مشابهی دارد - به هر کدام یک سهم می رسد.
توزیع اقلام (Distributing items) یک عمل است که طی آن اقلام را به صورت برابر گسترش می دهیم. توزیع جبری (Algebraic distribution) به این معنا می باشد که هر کدام از جملات داخل پرانتزها را در جمله دیگری که در بیرون پرانتز قرار دارد، ضرب کنیم. هر جمله در یک مقدار یکسان ضرب می گردد.
قوانین جبر: برای توزیع یک جمله روی چند جمله دیگر، هر کدام از آن جملات دیگر را در جمله اول ضرب کنید. توزیع به معنای ضرب کردن هر جمله منحصر بفرد از یک سری جمله گروه بندی شده در یک مقدار که در خارج از آن گروه بندی قرار دارد، می باشد.
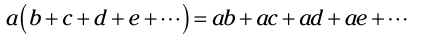
علامتهای جمع می توانستند تفریق باشند، و a می تواند هر عدد حقیقی باشد: مثبت، منفی، عدد صحیح، کسر.
علامتهای جمع می توانستند تفریق باشند، و a می تواند هر عدد حقیقی باشد: مثبت، منفی، عدد صحیح، کسر.
یادتان باشد: یک جمله (term) تشکیل شده است از متغیرها و/یا اعداد که با ضرب و/یا تقسیم به یکدیگر متصل شده اند. جملات با علامتهای جمع و تفریق از یکدیگر جدا می شوند.
مثال: عدد 2 را در عبارت زیر توزیع کنید:
وقتیکه چند فاکتور را در چندین جمله توزیع می کنید، مقدار عبارت اصلی را تغییر نمی دهید. خواه اینکه ابتدا توزیع را انجام بدهید یا اینکه ابتدا چیزهای داخل پرانتزها را با یکدیگر جمع بزنید، پاسخ یکسان است. هنگامی که دستکاری های جبری (algebraic manipulations) را انجام می دهید، اغلب مجبور می شوید که بر اساس تجربیات قبلیتان در جبر، یک تصمیم سرنوشت ساز بگیرید که آیا ابتدا چیزهای داخل پرانتز را با هم ترکیب کنید یا ابتدا توزیع را انجام بدهید.
نکته: توزیع در ابتدا (Distributing first) برای رسیدن به پاسخ در صورتی انتخاب بهتری است که دستکاری هر جمله اعداد زیباتری را به شما بدهد. گاهی اوقات اگر توزیع در ابتدا انجام شود، کسرها یا اعداد اعشاری داخل پرانتزها به اعدادی کامل و زیبا تبدیل می شوند. انتخاب دیگر - ترکیب عبارتهای داخل پرانتز در ابتدا - زمانی ترجیح داده می شود که توزیع به شما مسائل ضرب خیلی بزرگی را بدهد. گاهی اوقات گفتن اینکه مورد شما از کدام نوع می باشد، آسان است، در زمانهای دیگر، شما باید صرفاً حدس بزنید و آن را امتحان کنید.
توزیع در ابتدا (Distributing first)
گاهی اوقات شما صرفاً با نگاه کردن می توانید بگویید که آیا ساده تر اینست که ابتدا جمله بیرون پرانتز را توزیع کنید یا اینکه ابتدا عبارات داخل پرانتز را ترکیب کنید. یک لحظه صبر کردن و فکر کردن به اینکه کدام رویکرد می تواند بهتر باشد ممکن است در بلند مدت در زمان شما صرفه جویی کند.
مثال: با پیدا کردن حاصلضرب این عبارت را ساده کنید:
ببینید اگر شما بعد از اینکه کسرها را با یکدیگر جمع زدید، 60 را در
اکنون به انتخاب بهتر بنگرید، جایی که ابتدا توزیع انجام می شود:
با ضرب کردن در 60 از شر تمامی کسرها خلاص می شوید، بنابراین نیازی به پیدا کردن مخرج مشترک هم ندارید.
آیا مزایای توزیع در ابتدا را در این مورد دیدید؟ برای یک مثال از وضعیتی که جمع زدن در ابتدا بهتر می باشد، بخش بعدی را ببیند.
جمع زدن در ابتدا (Adding first)
قبل از شروع مراحل حل کردن یک مسأله توزیع، به اندازه اعداد نگاه کنید. اگر اعداد بزرگ باشند، سپس توزیع یک جمله بزرگ روی یک جمله بزرگتر دیگر در داخل پرانتزها صرفاً می تواند منجر به این شود که هر جمله بزرگتر شود و کمتر قابل مدیریت باشد. در مورد اعداد بزرگ، ممکن است ساده تر باشد که کار را از انجام جمع و تفریق های ساده در داخل پرانتزها شروع کنید، و سپس جمله بیرون پرانتز را بر روی موارد داخل پرانتز توزیع کنید.
مثال: این عبارت را ساده کنید:
اگر بخواهیم اول 43 را توزیع کنیم (اوه چه کاری!):
حالا به انتخاب بهتر بنگرید، جاییکه ابتدا عبارتهای داخل پرانتز را ترکیب می کنید:
یادتان باشد: مثالهای این بخش و بخش قبلی کمی اغراق آمیز هستند، اما من تعمداً برای روشن شدن موضوع اینطور مثال زدم. بهترین مسیر برای انتخاب همواره واضح نیست. اما اگر چشمانتان را باز نگه دارید و با دقت به انتخابهایتان بنگرید، می توانید در زمان و انرژی صرفه جویی کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: