خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توزیع متغیرها (Distributing variables)

توزیع متغیرها (Distributing variables) بر روی جملات موجود در یک عبارت جبری شامل قوانین ضرب و قوانین توانها می باشد. هنگامی که متغیرهای متفاوت در یکدیگر ضرب می شوند، می توانند کنار همدیگر نوشته شوند و نیاز هم نیست بین آنها علامت ضرب باشد. اگر به عنوان بخشی ازتوزیع، متغیرهایی که در یکدیگر ضرب می شوند، یکسان باشند، سپس توانهای آنها با یکدیگر جمع می شود.

اجازه بدهید چندتا مسأله توزیع به شما نشان بدهم که شامل فاکتورهای توان دار می باشند.
مثال: متغیر a را در عبارتهای داخل پرانتز توزیع کنید: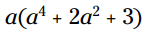
a را در هر جمله ضرب کنید:
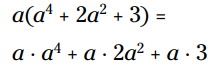
از قوانین توانها برای ساده سازی استفاده کنید:
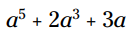
مثال: این عبارت را ساده کنید:
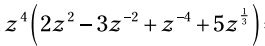
جمله z4 با ضرب کردن آن در هر جمله توزیع کنید:
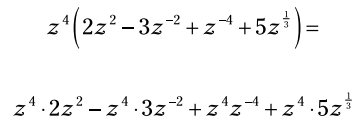
با جمع زدن توانها عبارت را ساده کنید:
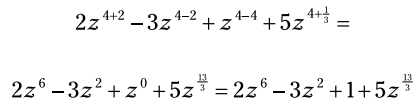
شما توانهای دارای علامت متفاوت را با قوانین جمع و تفریق اعداد علامت دار، با هم ترکیب می کنید. توانهای کسری بعد از پیدا کردن مخرج مشترک و بر اساس قوانین جمع و تفریق کسرها، با یکدیگر ترکیب می شوند. توانهایی که به شکل کسر نامتعارف (improper fraction) باشند، به همان شکل دست نخورده باقی می مانند و نیازی نیست تا آنها را به شکل عدد مختلط بنویسید.
مثال بعدی به شما نشان می دهد اگر بیش از یک متغیر داشته باشید چه اتفاقی می افتد - و چگونه باید از قوانین جمع زدن توانها خیلی بادقت استفاده کنید.
مثال: این عبارت را با توزیع ساده کنید:
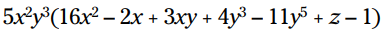
هر جمله را در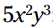 ضرب کنید:
ضرب کنید:
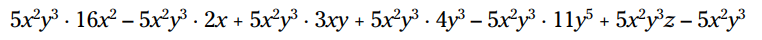
در هر جمله ضرب را تکمیل کنید. هر جا لازم باشد توانها را با یکدیگر جمع بزنید:
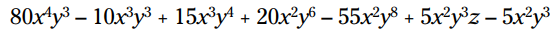
کار تمام شد! هیچ جمله مشابه دیگری برای ترکیب کردن یافت نمی شود.
مثال بعدی با اعداد منفی در هم آمیخته است.
مثال: این عبارت را با توزیع ساده کنید:

هر جمله را در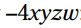 ضرب کنید:
ضرب کنید:
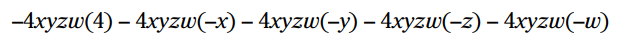
عملیات ضرب را در هر جمله تکمیل کنید:
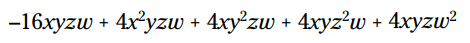
همانطور که عنوان این بخش نشان می دهد، یک پایه که دارای توان منفی باشد می تواند به یک کسر تبدیل شود. پایه و توان بخشی از مخرج کسر می شوند، اما در این فرآیند توان علامت منفی اش را از دست می دهد. در نهایت با قرار دادن 1 در صورت کسر کار را تمام می کنید.
در مثال بعدی، به شما نشان می دهم چگونه یک توان منفی به یک پاسخ کسری منجر می شود.
مثال: این عبارت را ساده کنید:
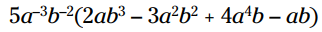
جمله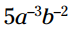 را در هر جمله داخل پرانتز توزیع کنید:
را در هر جمله داخل پرانتز توزیع کنید:
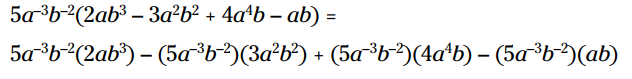
اعداد را در یکدیگر ضرب کنید و توانها را با هم جمع بزنید:

فاکتوری از b که توان آن 0 می باشد تبدیل به 1 می گردد:
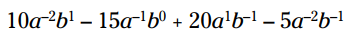
مرحله بعدی پاسخ نهایی را بدون توانهای منفی نشان می دهد - برای این کار از فرمول تبدیل توانهای منفی به کسرها استفاده شده است:
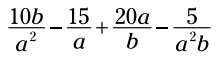
توانهایی که کسری می باشند به همان شیوه مشابه توانهای اعداد صحیح کار می کنند. هنگامی که فاکتورهای دارای پایه یکسان را در یکدیگر ضرب می کنید، توانها با یکدیگر جمع می شوند. تنها تفاوت در اینست که کسرها باید دارای مخرج یکسان باشند تا بتوانند با هم جمع زده شوند. (صرفاً به دلیل اینکه توانها کسری هستند، قوانین تغییری نمی کنند.)
مثال: این عبارت را توزیع و ساده کنید:
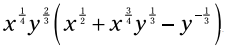
فاکتور را در هر جمله ضرب کنید:
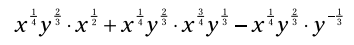
متغیرها را بازچینش کنید و توانها را با یکدیگر جمع بزنید:
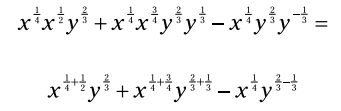
جمع زدن کسرها را تکمیل نمایید:
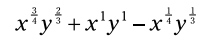
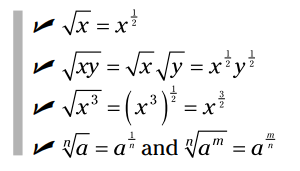
هنگامی که در مسأله رادیکال داشته باشید، اگر ابتدا همه چیز را به توان های کسری تبدیل کنید، توزیع ساده تر می گردد. (برای اطلاعات بیشتر در مورد توانها و رادیکال ها فصل 4 را ببینید.)
مثال: این عبارت را با توزیع ساده کنید:
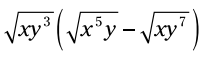
نمادهای رادیکال را به توان های کسری تبدیل کنید:
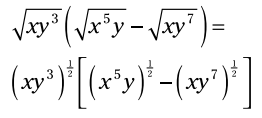
از قانون به توان رساندن توان استفاده کنید:
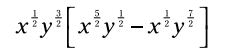
جمله بیرون پرانتز را بر روی هر جمله داخل پرانتز توزیع کنید:
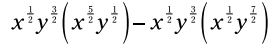
توانهای متغیرها را با یکدیگر جمع بزنید:
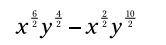
توان های کسری را ساده کنید:
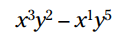

اجازه بدهید چندتا مسأله توزیع به شما نشان بدهم که شامل فاکتورهای توان دار می باشند.
مثال: متغیر a را در عبارتهای داخل پرانتز توزیع کنید:
a را در هر جمله ضرب کنید:
از قوانین توانها برای ساده سازی استفاده کنید:
مثال: این عبارت را ساده کنید:
جمله z4 با ضرب کردن آن در هر جمله توزیع کنید:
با جمع زدن توانها عبارت را ساده کنید:
یادتان باشد: توان 0 به این معنا می باشد که مقدار عبارت 1 می باشد. برای هر عدد حقیقی x داریم 1 = x0 ، مقدار x نمی تواند 0 باشد.
شما توانهای دارای علامت متفاوت را با قوانین جمع و تفریق اعداد علامت دار، با هم ترکیب می کنید. توانهای کسری بعد از پیدا کردن مخرج مشترک و بر اساس قوانین جمع و تفریق کسرها، با یکدیگر ترکیب می شوند. توانهایی که به شکل کسر نامتعارف (improper fraction) باشند، به همان شکل دست نخورده باقی می مانند و نیازی نیست تا آنها را به شکل عدد مختلط بنویسید.
مثال بعدی به شما نشان می دهد اگر بیش از یک متغیر داشته باشید چه اتفاقی می افتد - و چگونه باید از قوانین جمع زدن توانها خیلی بادقت استفاده کنید.
مثال: این عبارت را با توزیع ساده کنید:
هر جمله را در
در هر جمله ضرب را تکمیل کنید. هر جا لازم باشد توانها را با یکدیگر جمع بزنید:
کار تمام شد! هیچ جمله مشابه دیگری برای ترکیب کردن یافت نمی شود.
مثال بعدی با اعداد منفی در هم آمیخته است.
مثال: این عبارت را با توزیع ساده کنید:
هر جمله را در
عملیات ضرب را در هر جمله تکمیل کنید:
حاصل توانهای منفی پاسخهای کسری می شود
همانطور که عنوان این بخش نشان می دهد، یک پایه که دارای توان منفی باشد می تواند به یک کسر تبدیل شود. پایه و توان بخشی از مخرج کسر می شوند، اما در این فرآیند توان علامت منفی اش را از دست می دهد. در نهایت با قرار دادن 1 در صورت کسر کار را تمام می کنید.
یادتان باشد: فرمول تغییر دادن توان منفی به کسر این می باشد:
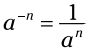 برای مشاهده اطلاعات بیشتر در این زمینه، فصل 4 را ببینید.
برای مشاهده اطلاعات بیشتر در این زمینه، فصل 4 را ببینید.
در مثال بعدی، به شما نشان می دهم چگونه یک توان منفی به یک پاسخ کسری منجر می شود.
مثال: این عبارت را ساده کنید:
جمله
اعداد را در یکدیگر ضرب کنید و توانها را با هم جمع بزنید:
فاکتوری از b که توان آن 0 می باشد تبدیل به 1 می گردد:
مرحله بعدی پاسخ نهایی را بدون توانهای منفی نشان می دهد - برای این کار از فرمول تبدیل توانهای منفی به کسرها استفاده شده است:
کار با توانهای کسری
توانهایی که کسری می باشند به همان شیوه مشابه توانهای اعداد صحیح کار می کنند. هنگامی که فاکتورهای دارای پایه یکسان را در یکدیگر ضرب می کنید، توانها با یکدیگر جمع می شوند. تنها تفاوت در اینست که کسرها باید دارای مخرج یکسان باشند تا بتوانند با هم جمع زده شوند. (صرفاً به دلیل اینکه توانها کسری هستند، قوانین تغییری نمی کنند.)
مثال: این عبارت را توزیع و ساده کنید:
فاکتور را در هر جمله ضرب کنید:
متغیرها را بازچینش کنید و توانها را با یکدیگر جمع بزنید:
جمع زدن کسرها را تکمیل نمایید:
یادتان باشد: رادیکال ها (Radicals) می توانند به عباراتی با توانهای کسری تبدیل گردند. این موضوع در زمانیکه می خواهید جملاتی را که دارای پایه یکسان می باشند با یکدیگر ترکیب کنید و برخی پایه ها زیر رادیکال می باشند، سودمند می باشد.
هنگامی که در مسأله رادیکال داشته باشید، اگر ابتدا همه چیز را به توان های کسری تبدیل کنید، توزیع ساده تر می گردد. (برای اطلاعات بیشتر در مورد توانها و رادیکال ها فصل 4 را ببینید.)
مثال: این عبارت را با توزیع ساده کنید:
نمادهای رادیکال را به توان های کسری تبدیل کنید:
از قانون به توان رساندن توان استفاده کنید:
جمله بیرون پرانتز را بر روی هر جمله داخل پرانتز توزیع کنید:
توانهای متغیرها را با یکدیگر جمع بزنید:
توان های کسری را ساده کنید:
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: